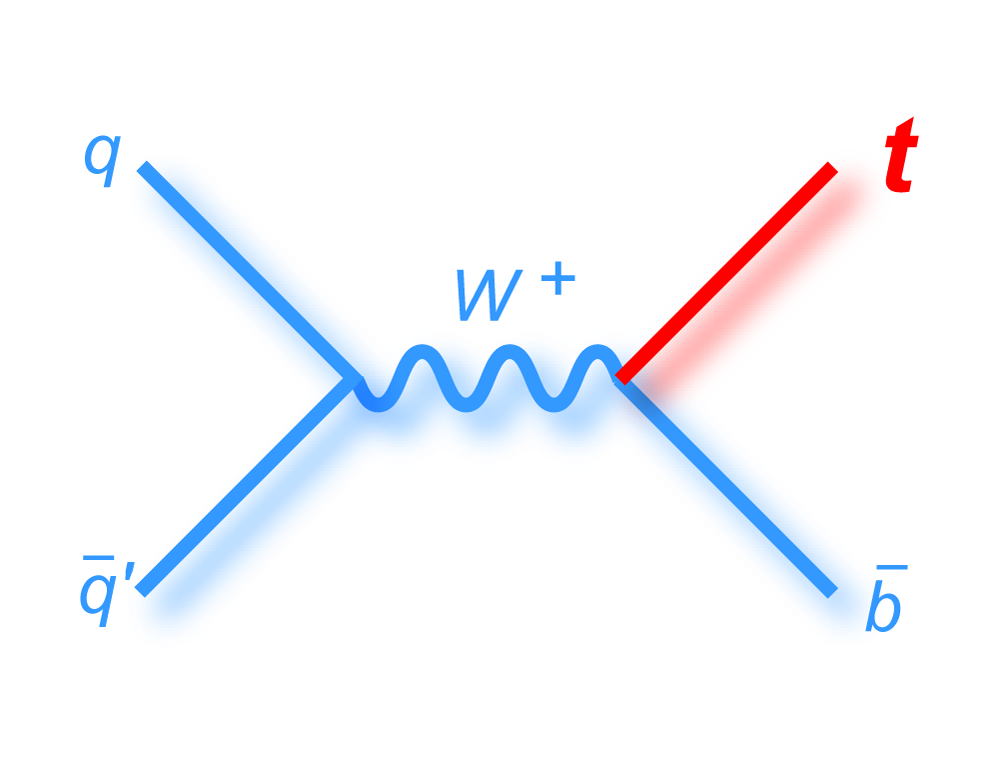
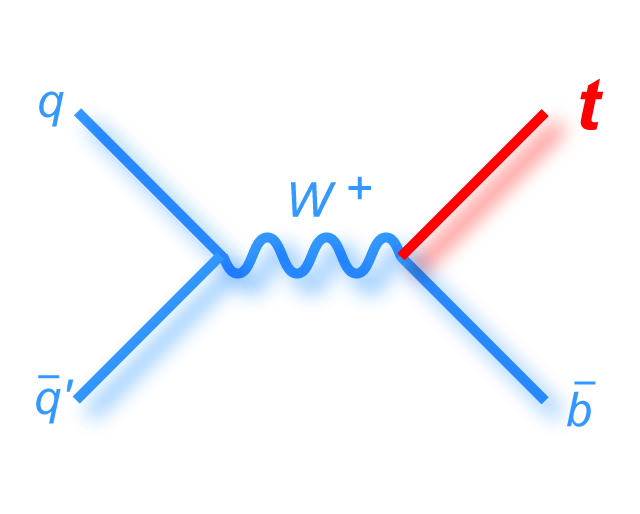
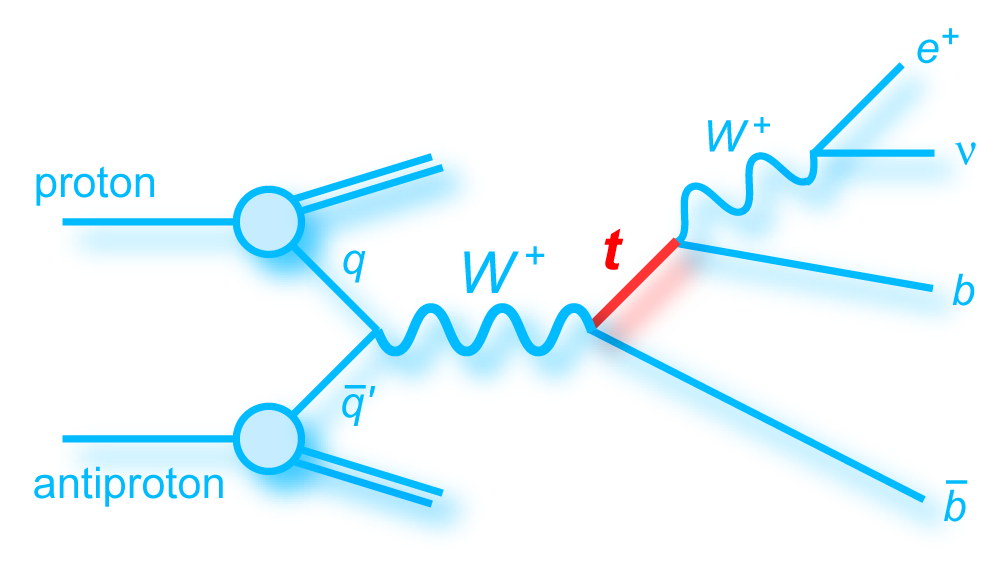
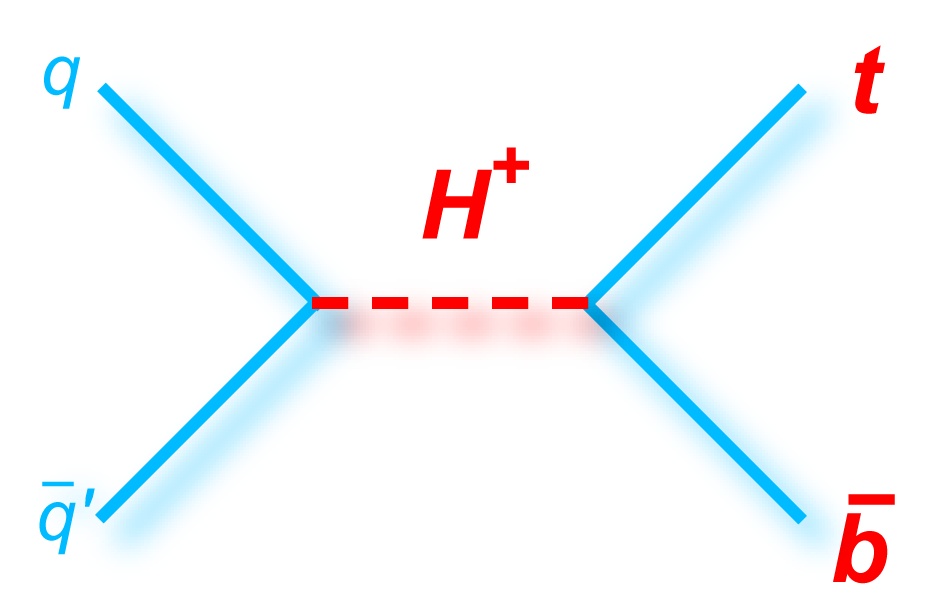
 s-channel "tb" |
|
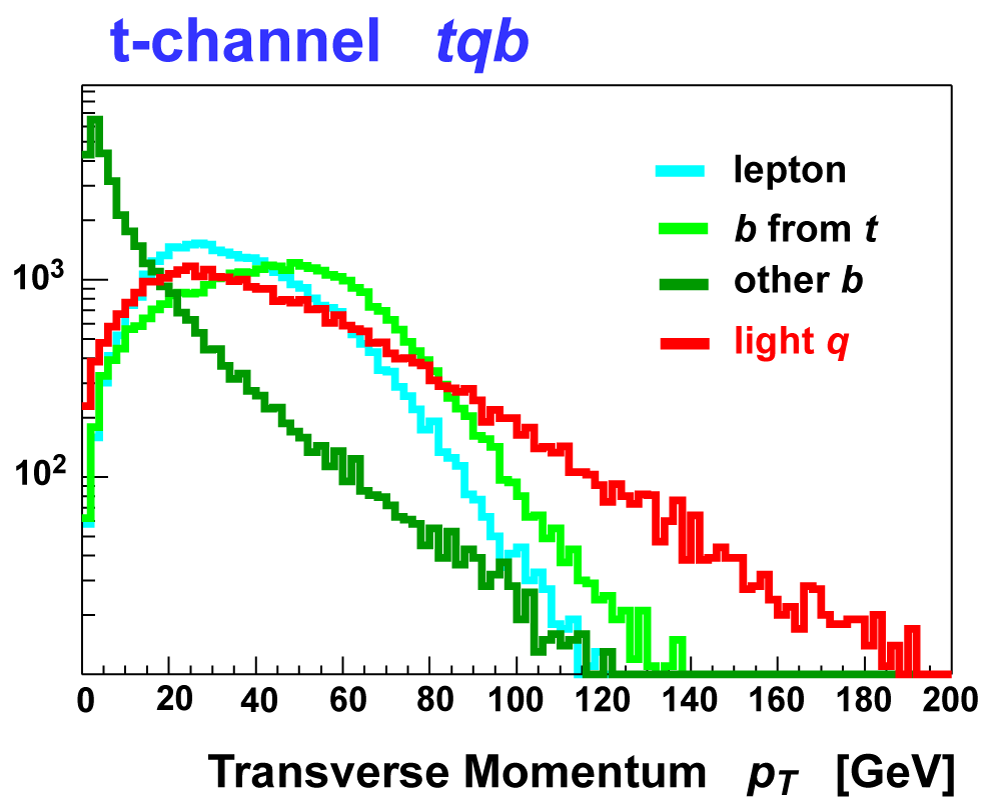
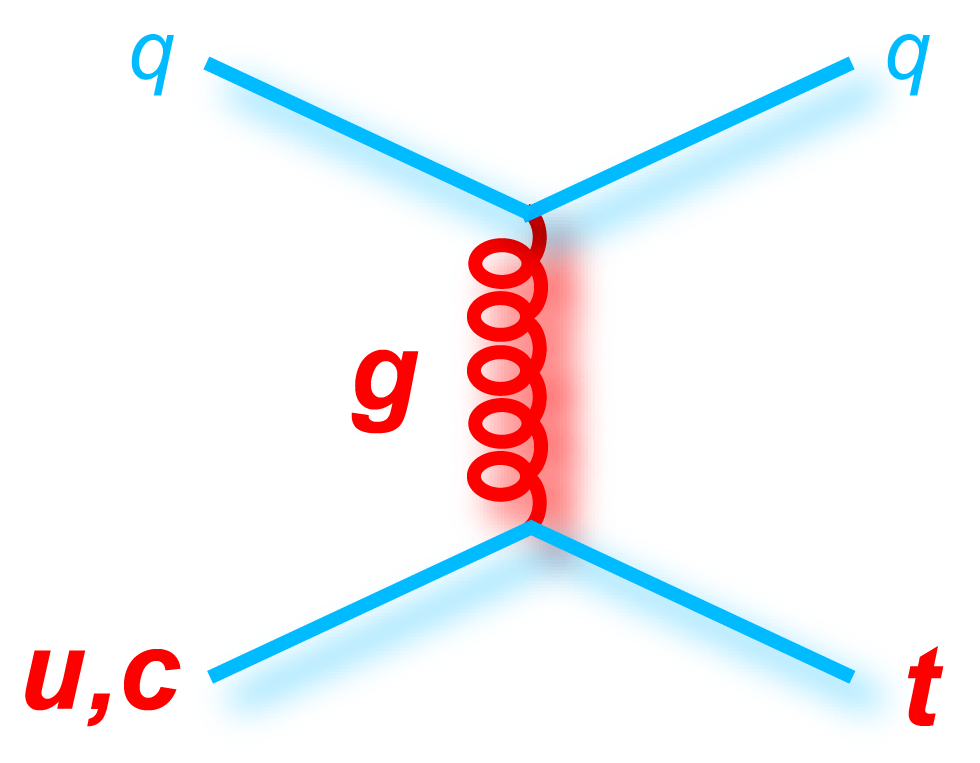
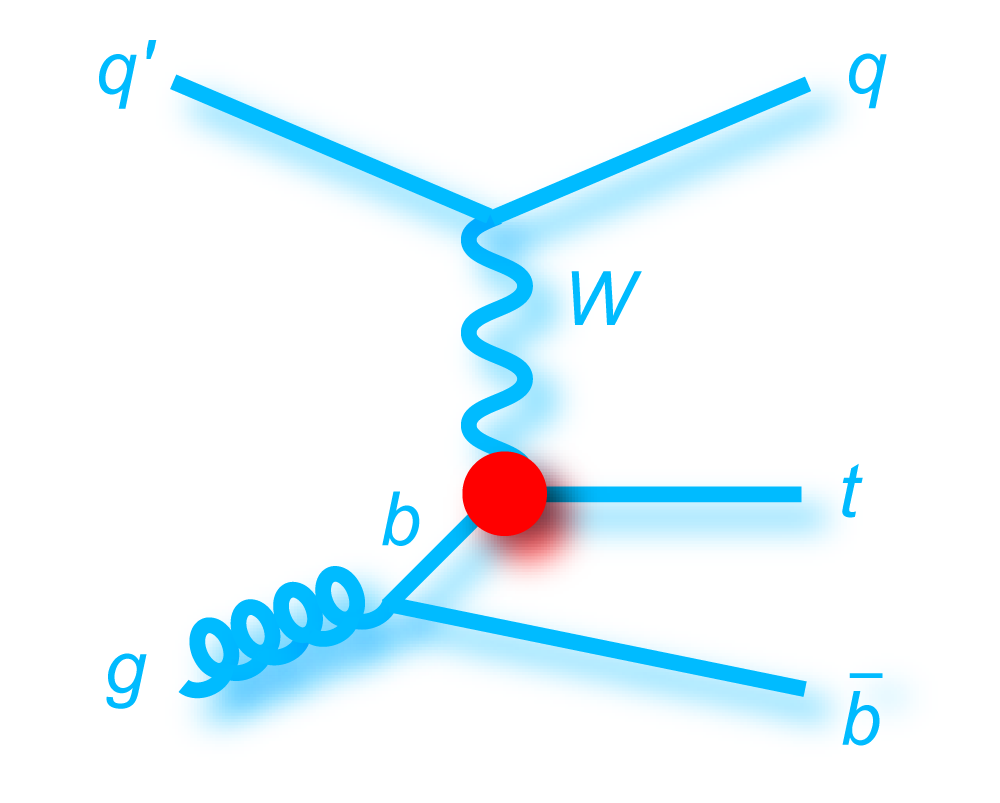
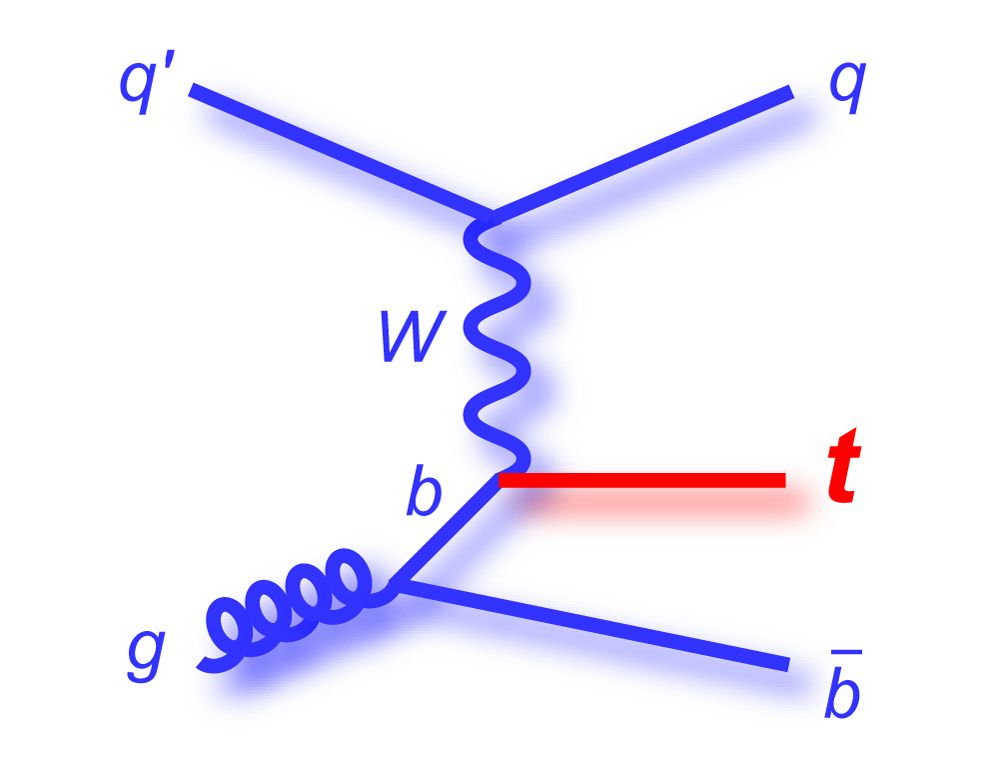 t-channel "tqb" |
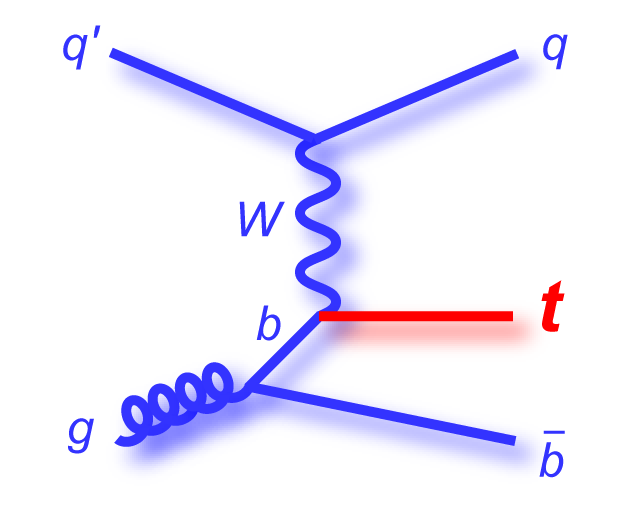
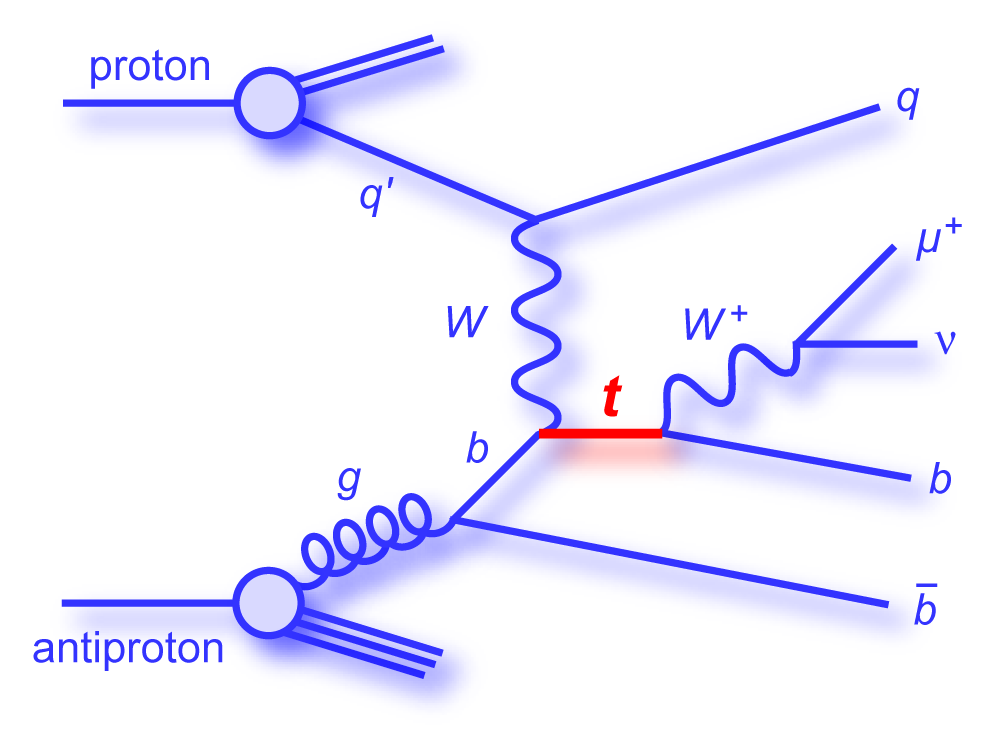
 s-channel "tb" |
|
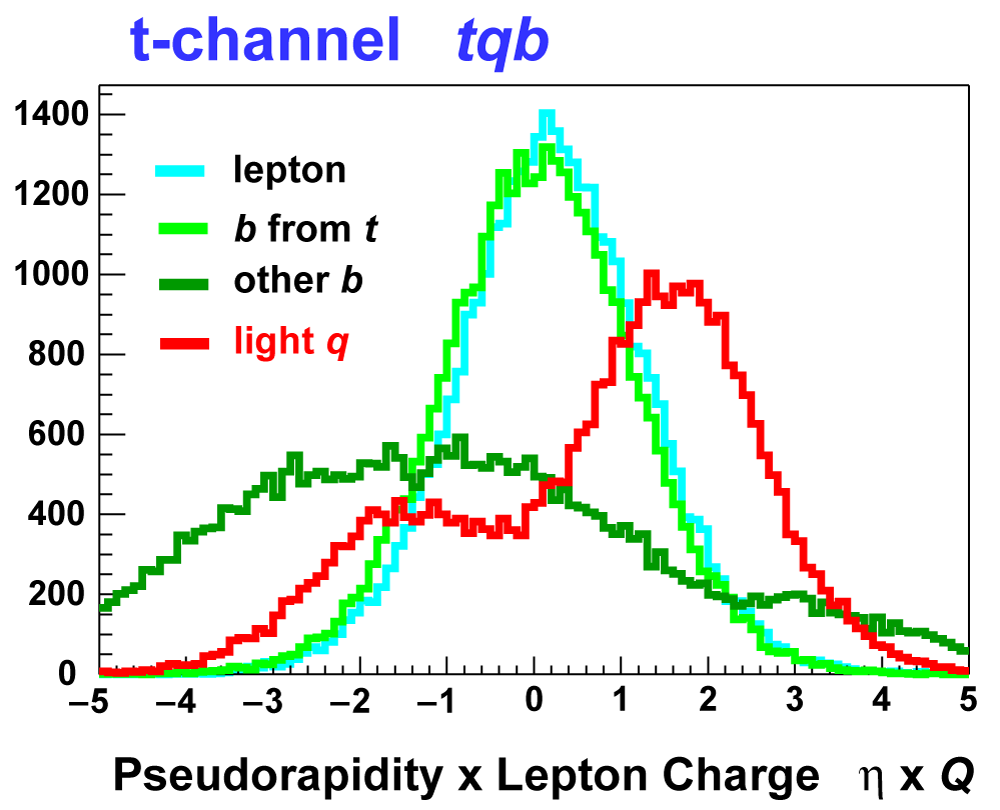
 t-channel "tqb" |
|
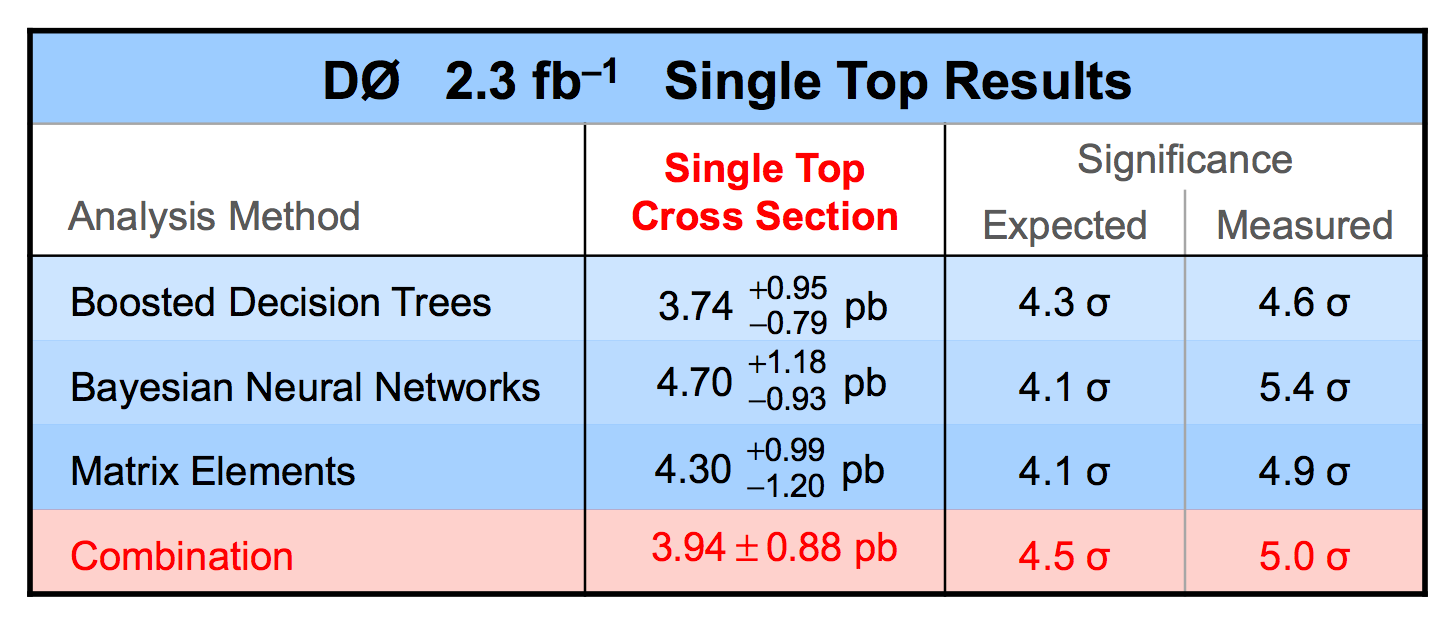
Abstract Event Selection Systematic Uncertainties Signal-Background Discrimination |
Combination of Results Signal Plots CKM Matrix Element Vtb Observation Summary |
Talks In the News More Images for Talks Contacts |
|
|
(Click on a link to jump down the page) |
|||
| The analysis is performed using a top quark mass of 170 GeV, which is close to the published world average value (171.2 GeV, Particle Data Book 2008 edition). The theoretical predictions for the cross sections of the two modes of single top quark production are 1.12 ± 0.04 pb for the s-channel tb mode and 2.34 ± 0.12 pb for the t-channel tqb mode (N. Kidonakis, Phys. Rev. D 74, 114012 (2006) with NNNLO-NLO matching, for mtop = 170 GeV and MRST2004 NNLO parton distribution functions). We do not use these values in the tb+tqb cross section measurement directly, but we assume the SM ratio of the processes, 1.12 : 2.34 = 1 : 2.1 when measuring the signal acceptance, selecting events used to train the BDT and BNN discriminants, and generating pseudo-datasets for the linearity tests. |
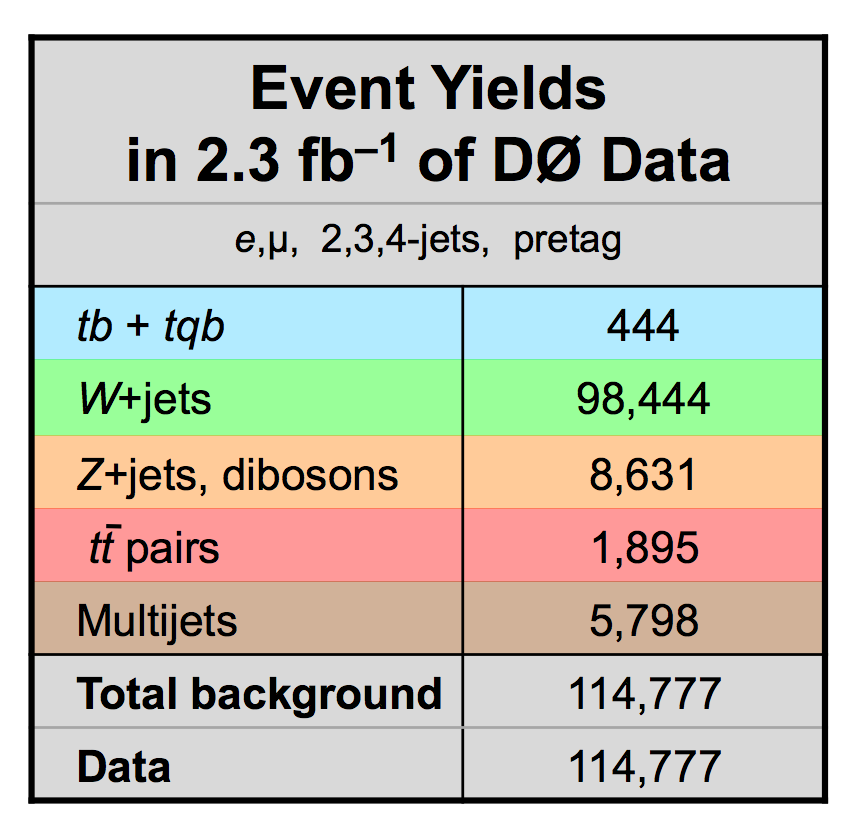
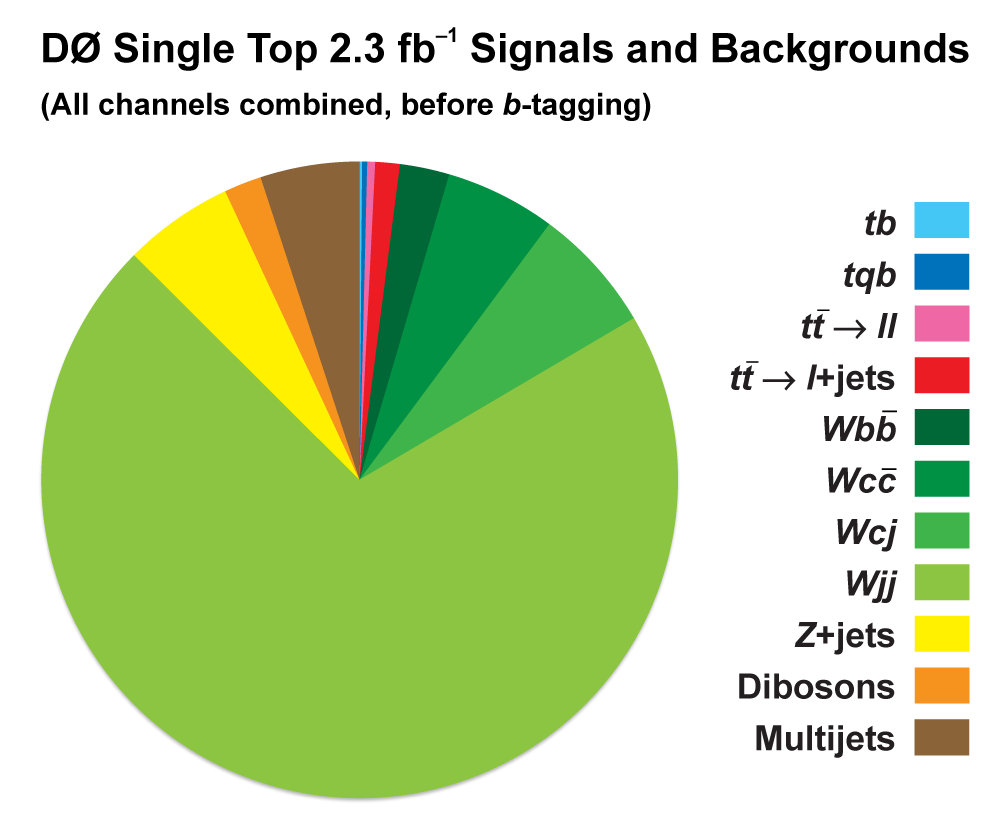
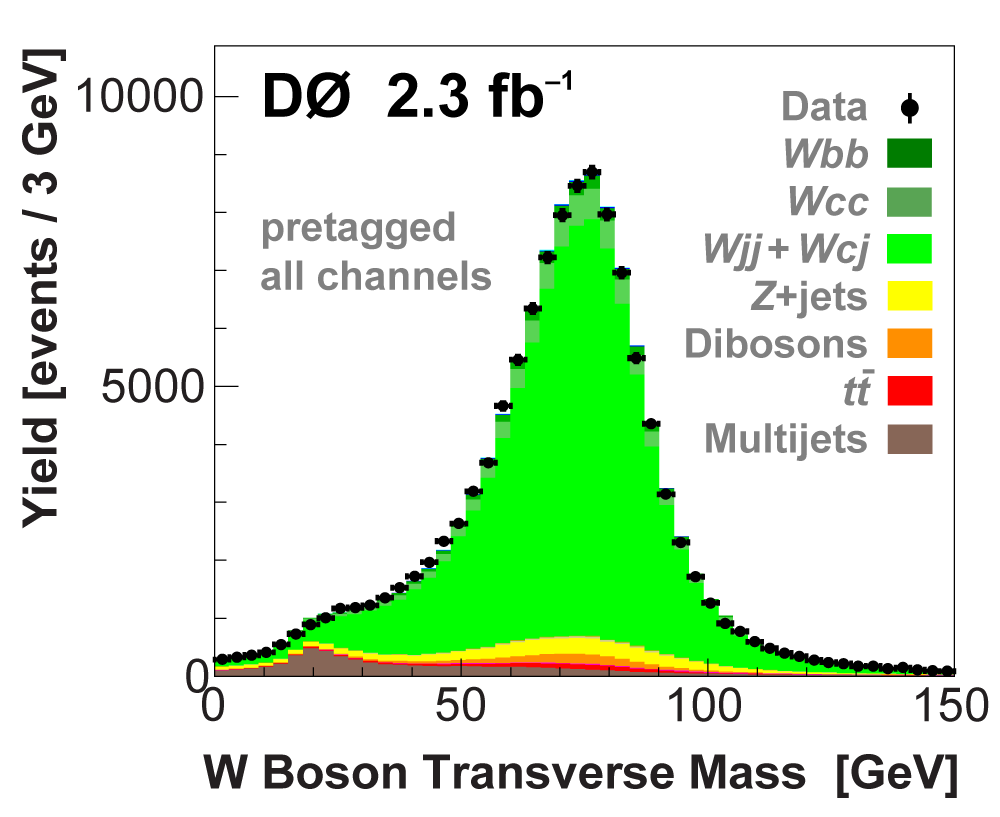
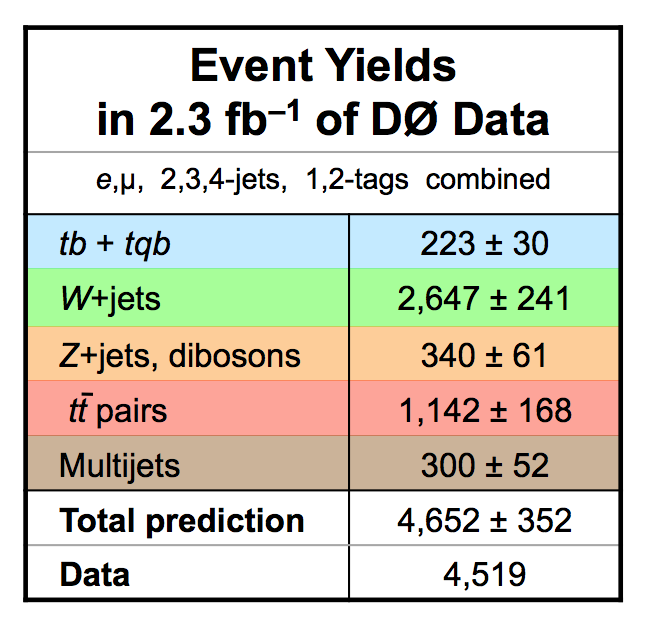
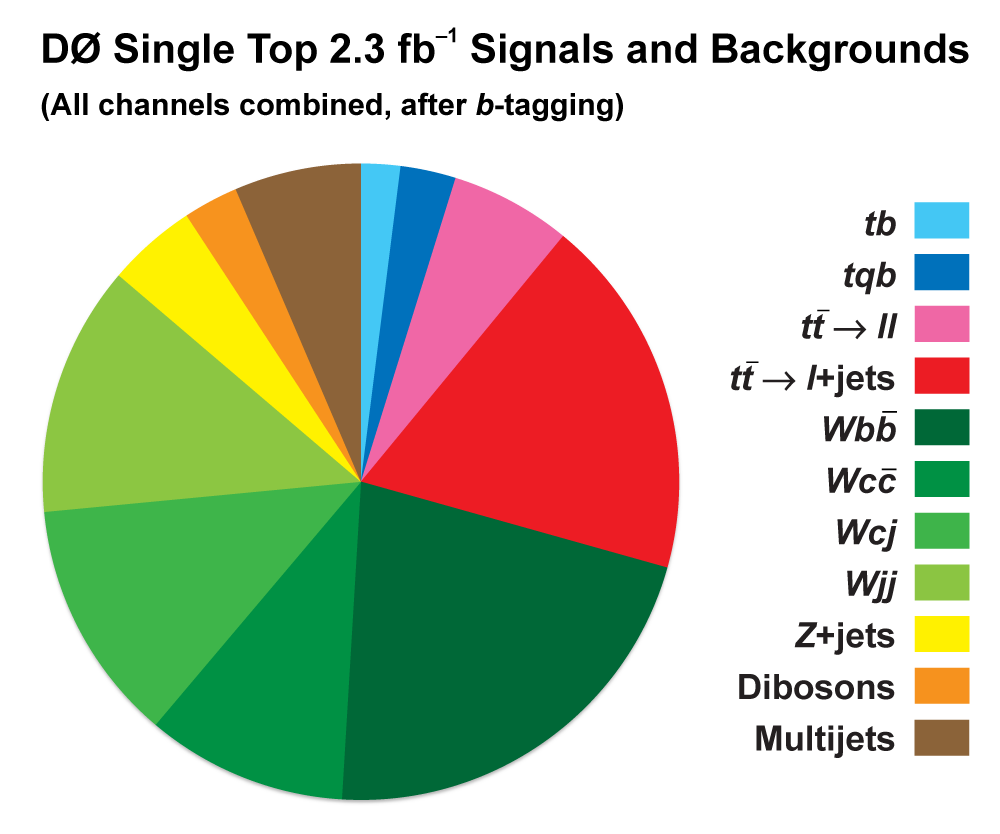
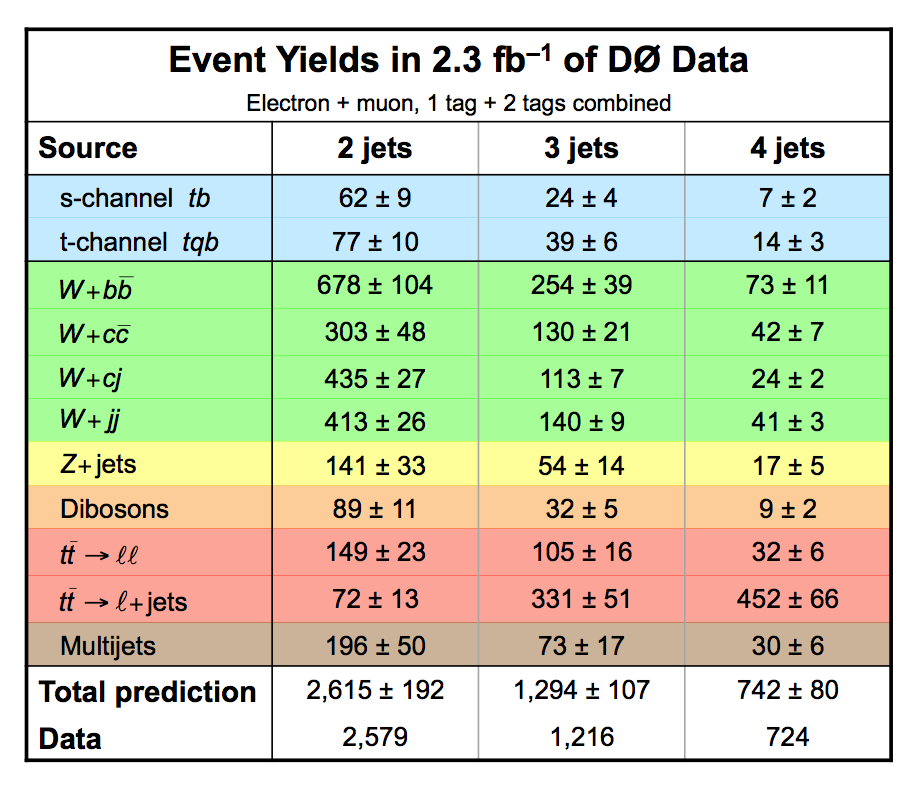
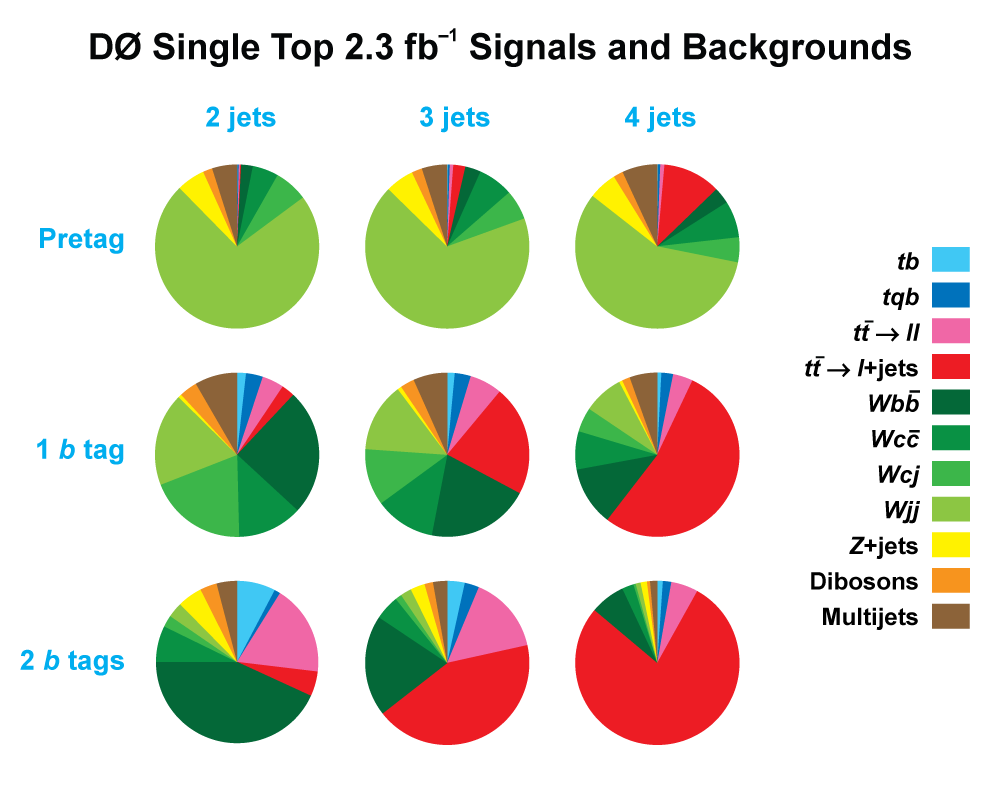
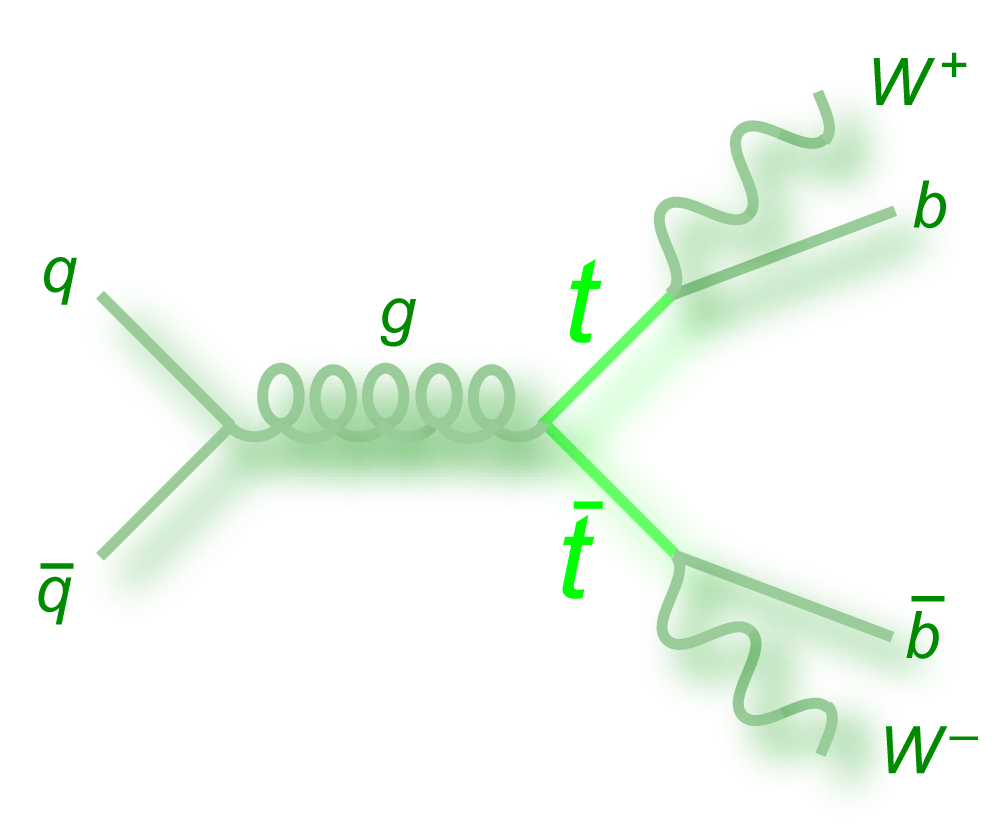
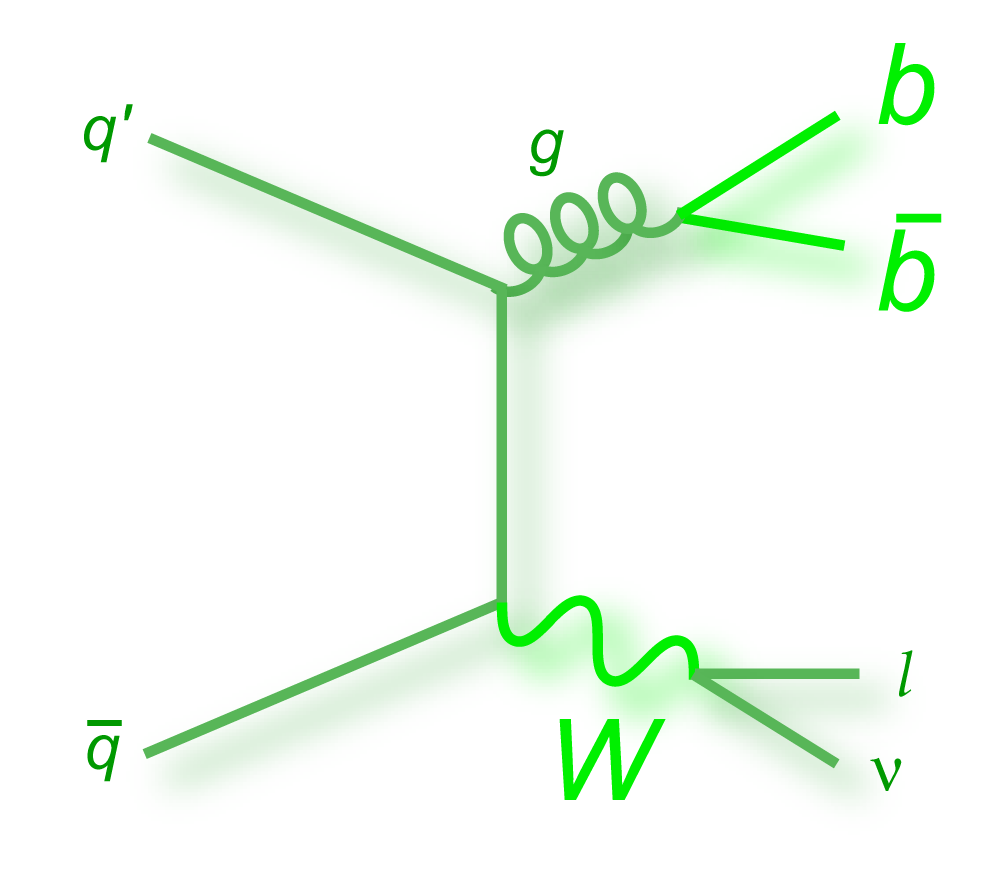
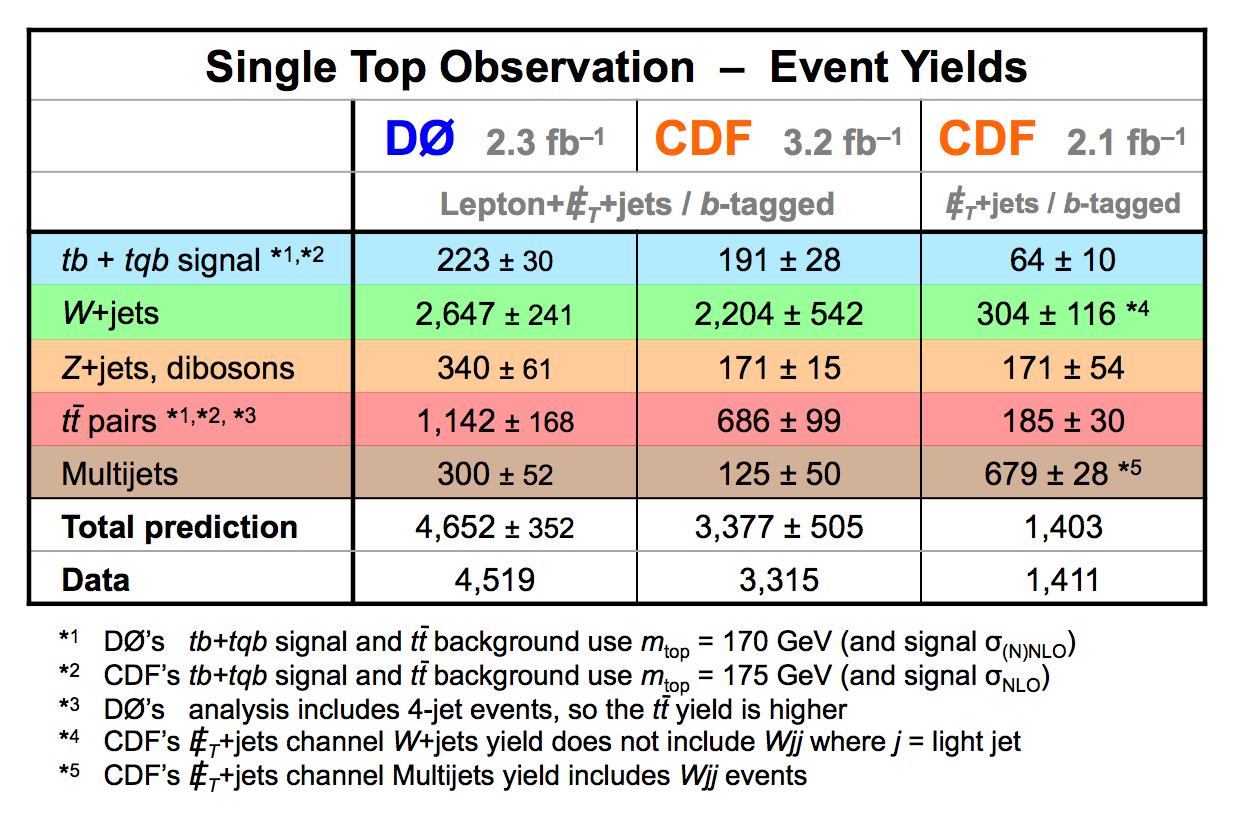
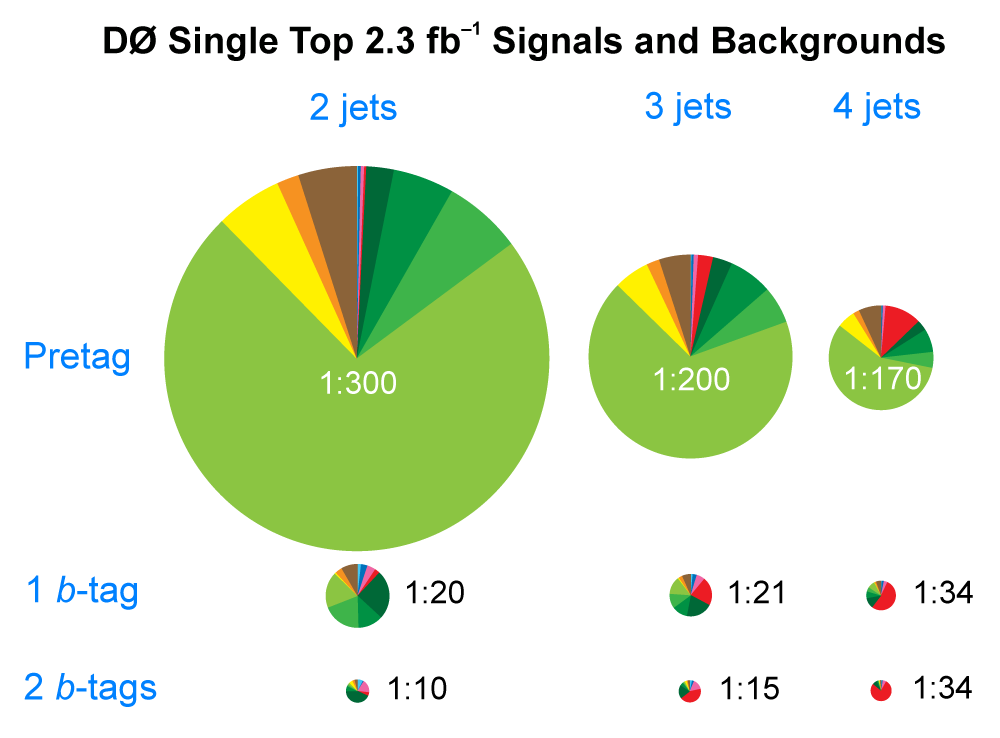
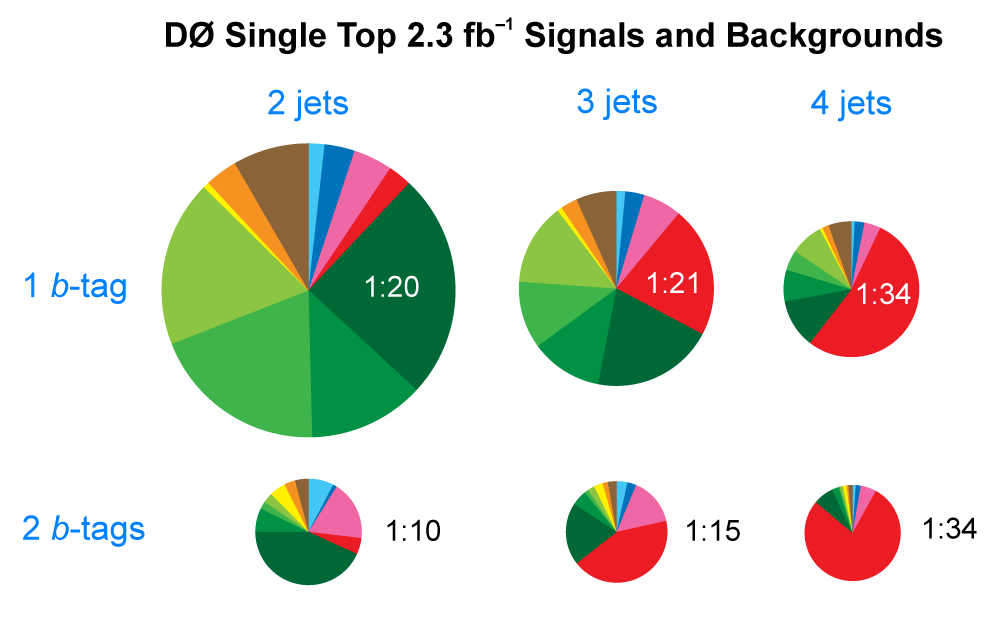
| The measurement uses data that pass almost any online trigger for maximum efficiency. We require between two and four jets, exactly one high transverse momentum electron or muon isolated from all jets in the event, and high missing transverse energy. One or two of the jets must be b-tagged. We model the single-top signal using the COMPHEP-SINGLETOP event generator coupled to PYTHIA for the underlying event and jet fragmentation. We model the tt, W+jets, and Z+jets using ALPGEN with PYTHIA using parton-jet matching. The small diboson (WW, WZ, ZZ) backgrounds are modeled with PYTHIA and the small multijet backgrounds where a jet has faked an electron, or a muon from b decay has traveled wide of its jet, is modeled using data. The tt, Z+jets, and diboson backgrounds are normalized to the theory cross sections, and the W+jets and multijets backgrounds are normalized to data. The resulting event yields are shown in the tables below. The proportions of signal and background predicted in the data before and after b-tagging are shown in the pie charts. After event selection, the signal acceptances (percentage of total cross section that pass the cuts) are (3.7 ± 0.5)% for the s-channel tb process and (2.5 ± 0.3)% for the t-channel tqb process. (The t-channel process has a lower acceptance because the second b-jet has low transverse momentum and is difficult to identify. These acceptances are ~18% higher than in our previous analysis, mainly because of the change in choice of triggers from lepton+jets ones only to allowing data events to pass almost any trigger. This analysis uses 85 million Monte Carlo events. After event selection, we have 0.5 million MC signal events, 1.4 million W+jets events, 1.6 million tt, a few hundred thousand Z+jets and diboson events, (4.1 million MC events in total), and 0.8 million pretagged multijets data events (31 thousand with b-tags). |
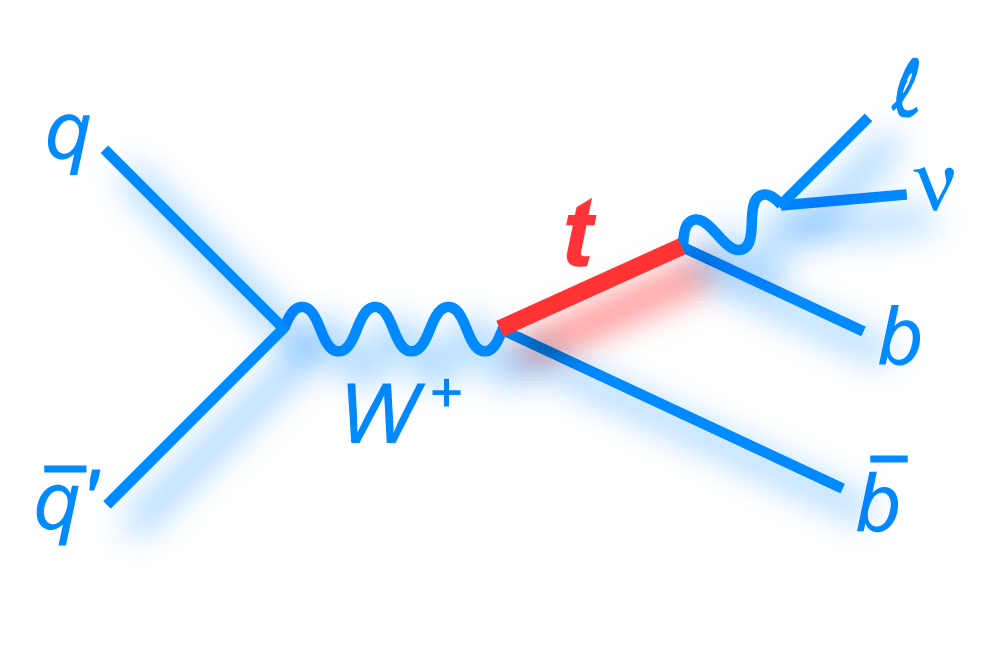 |
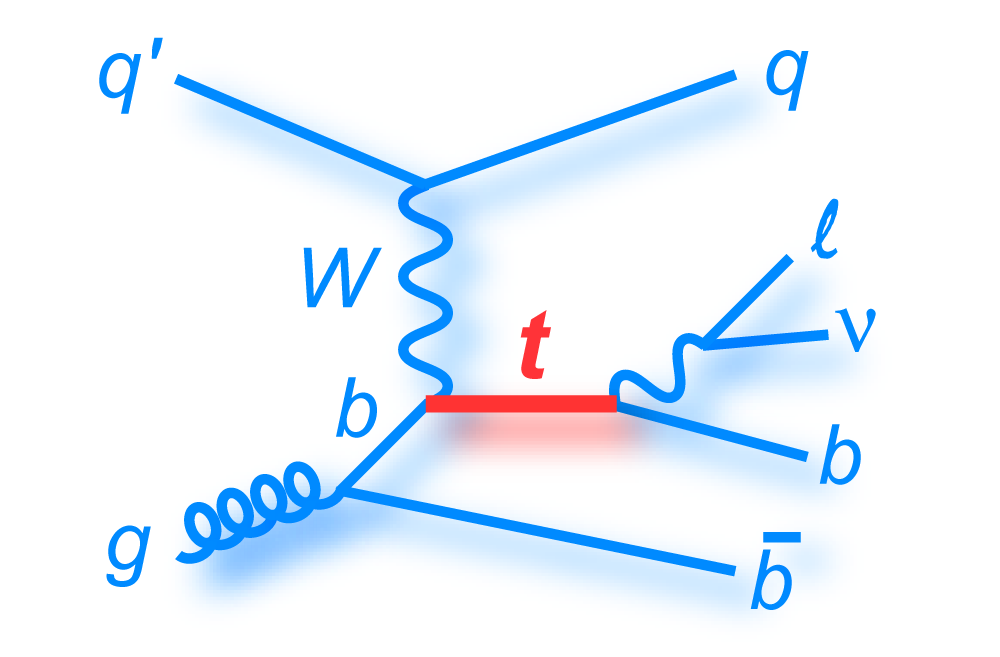 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
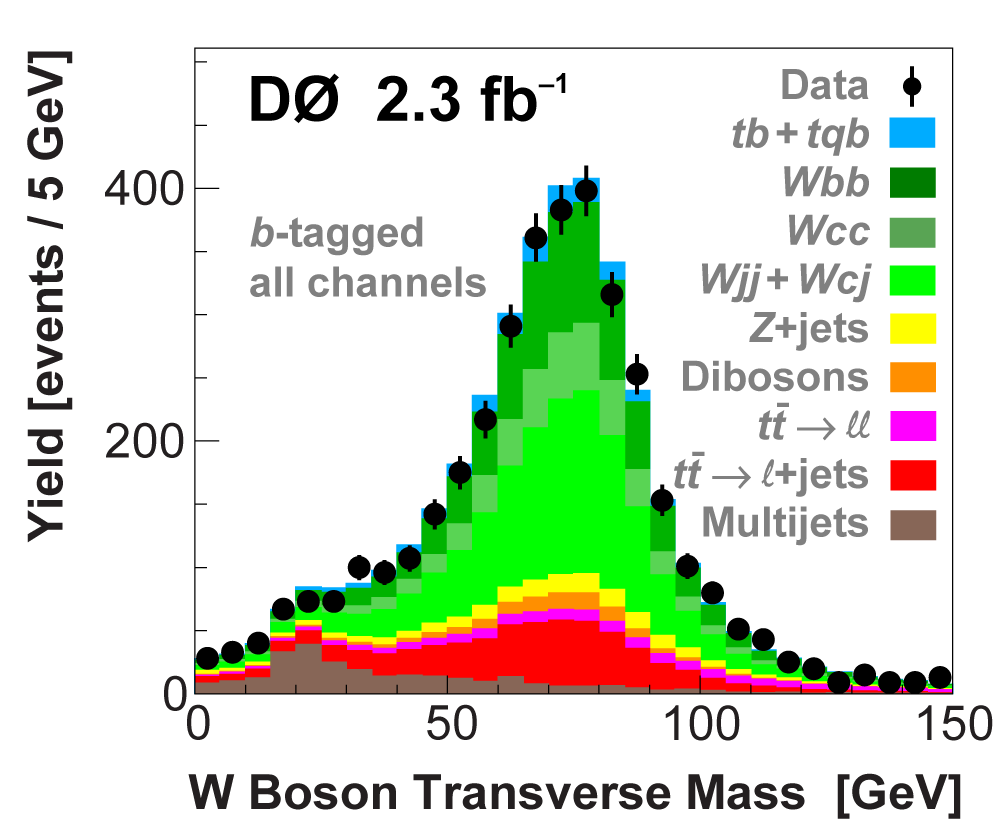
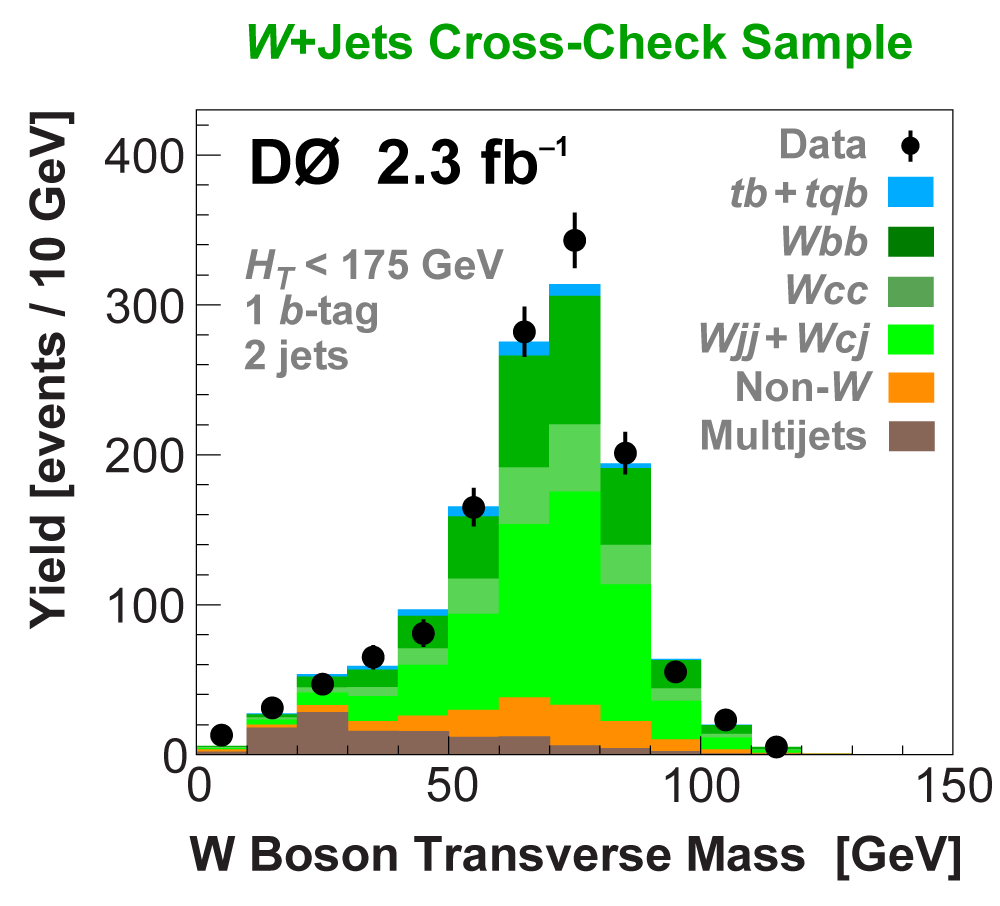
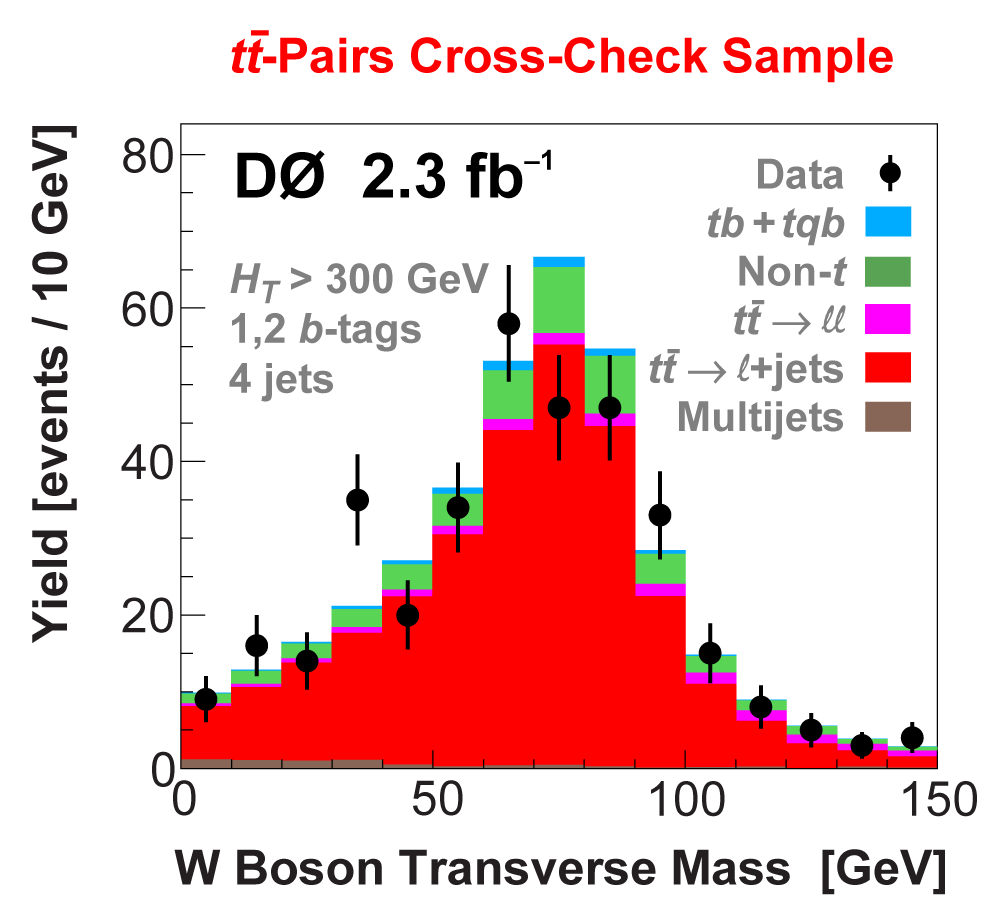
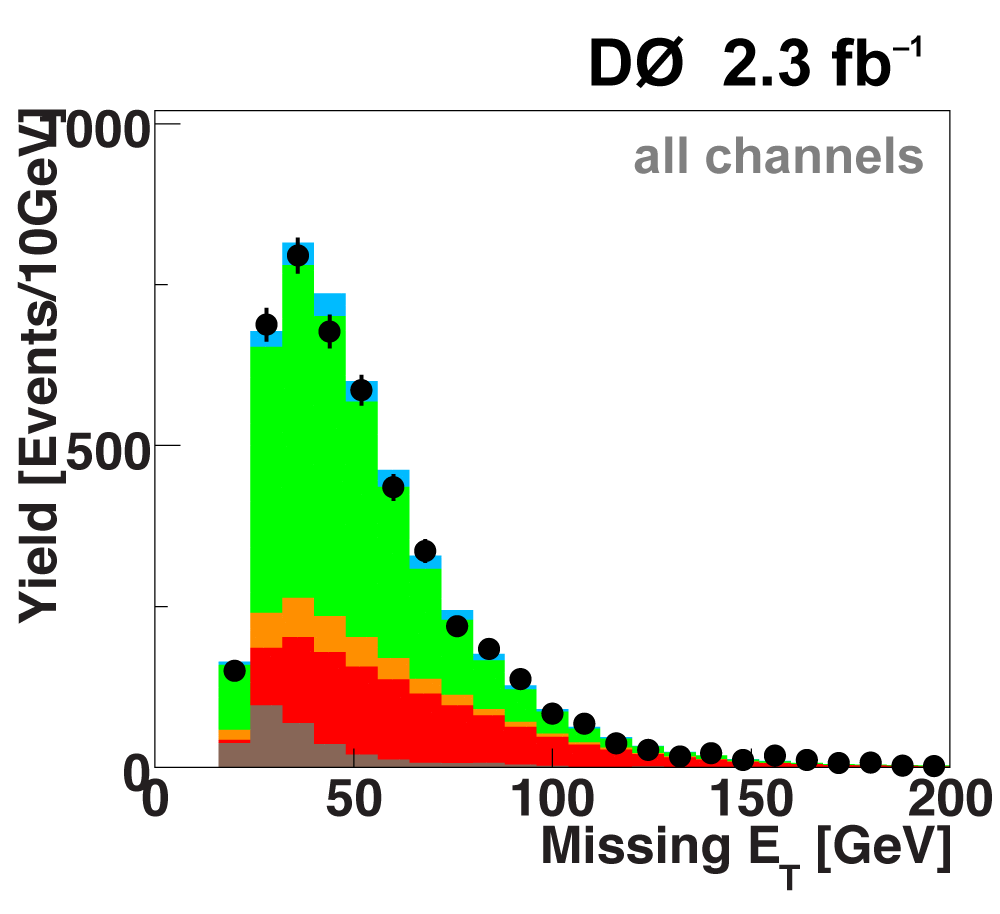
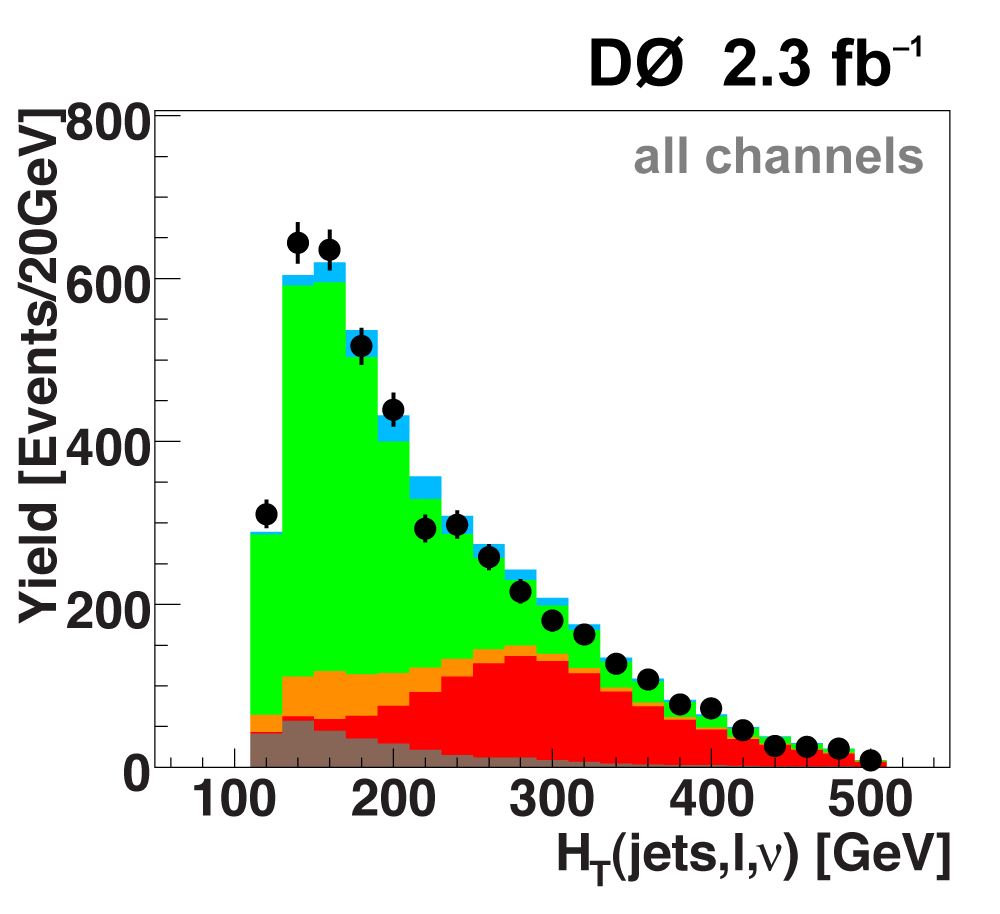
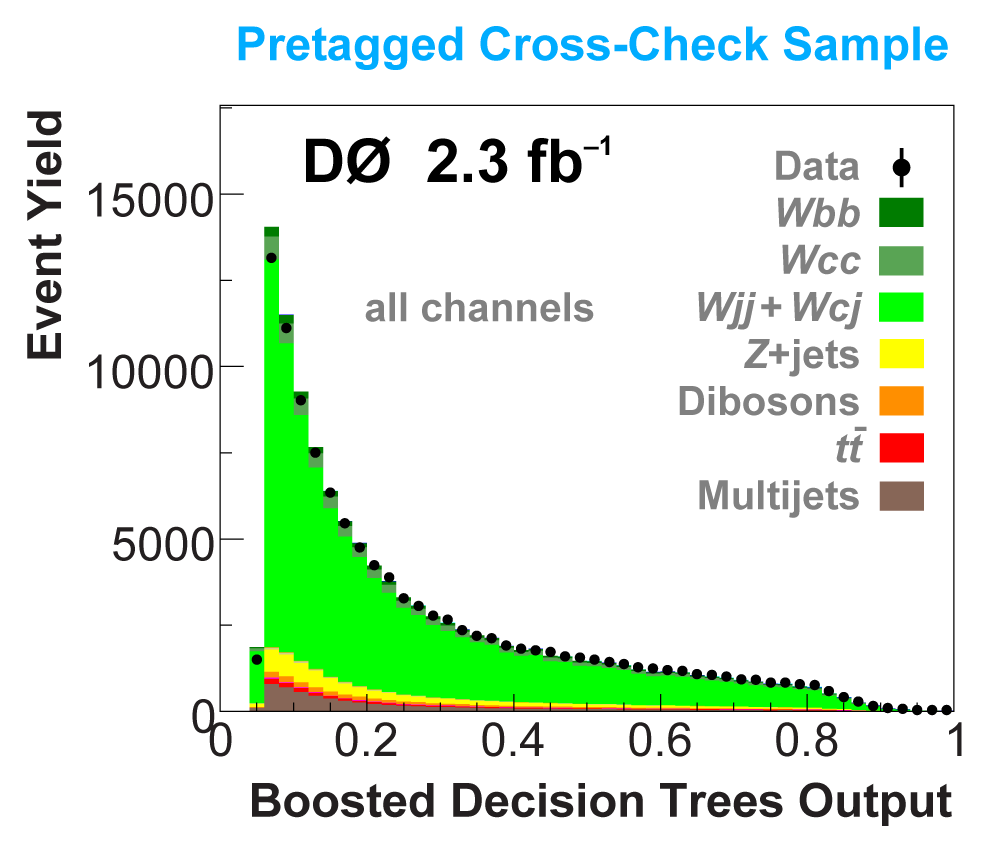
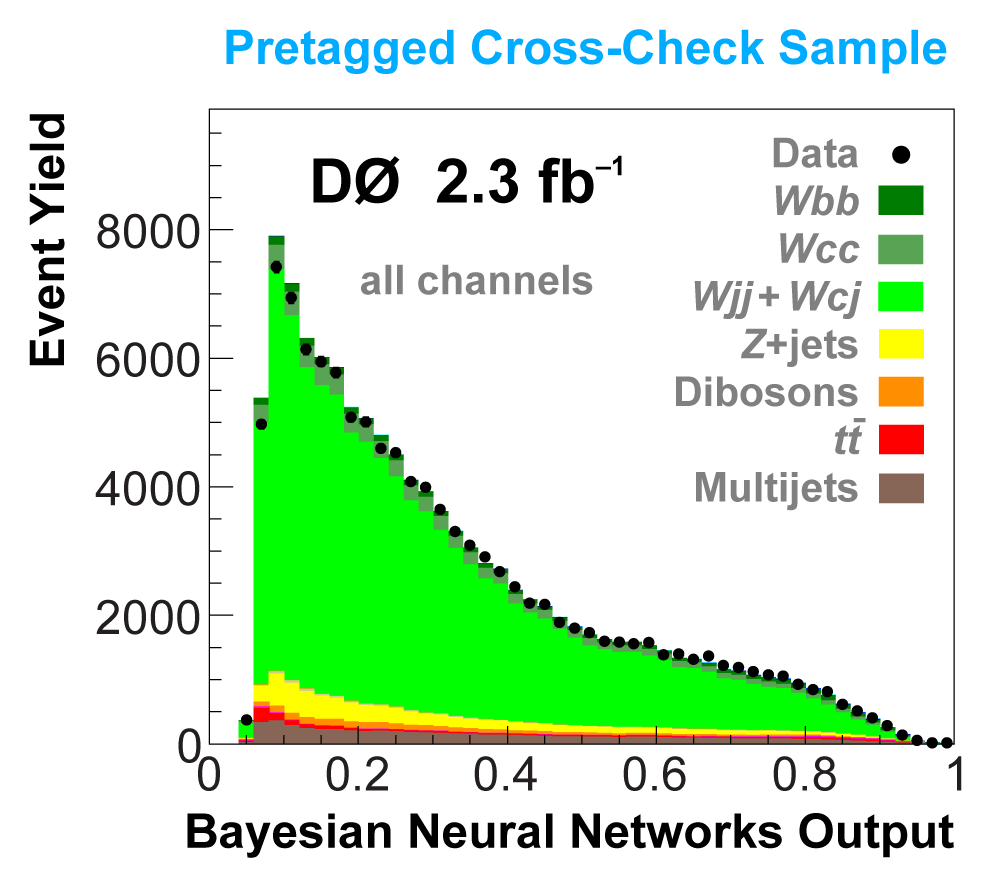
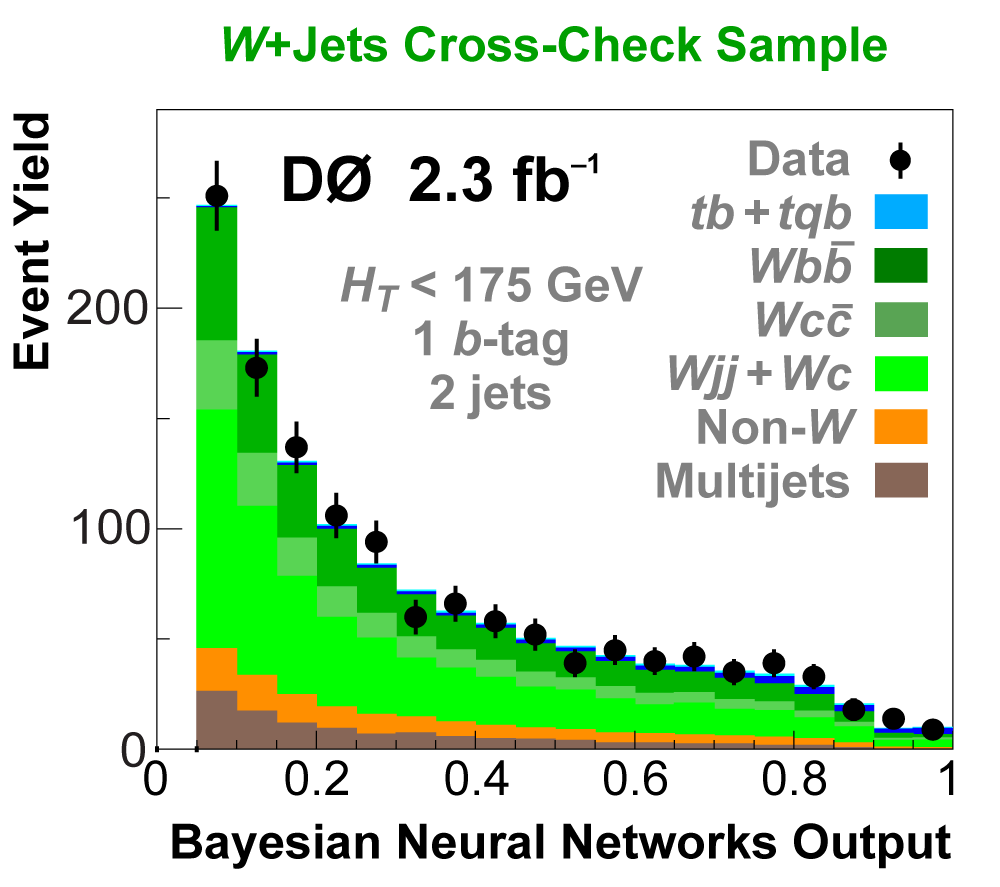
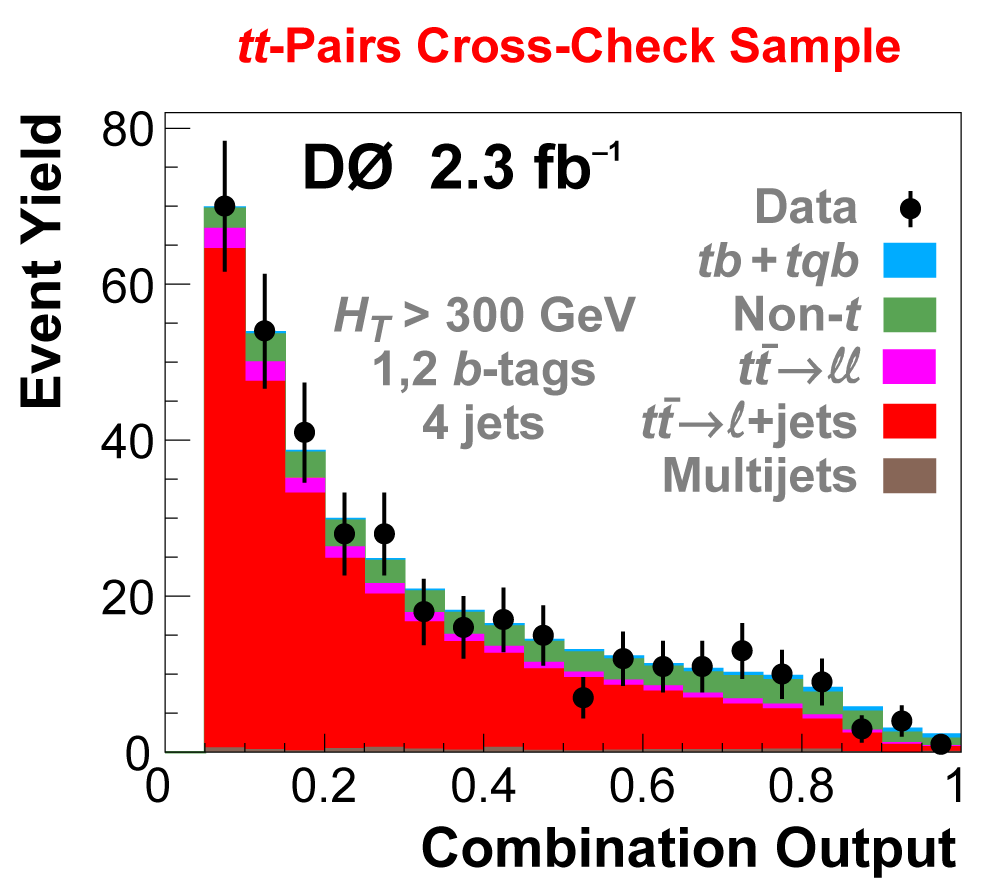
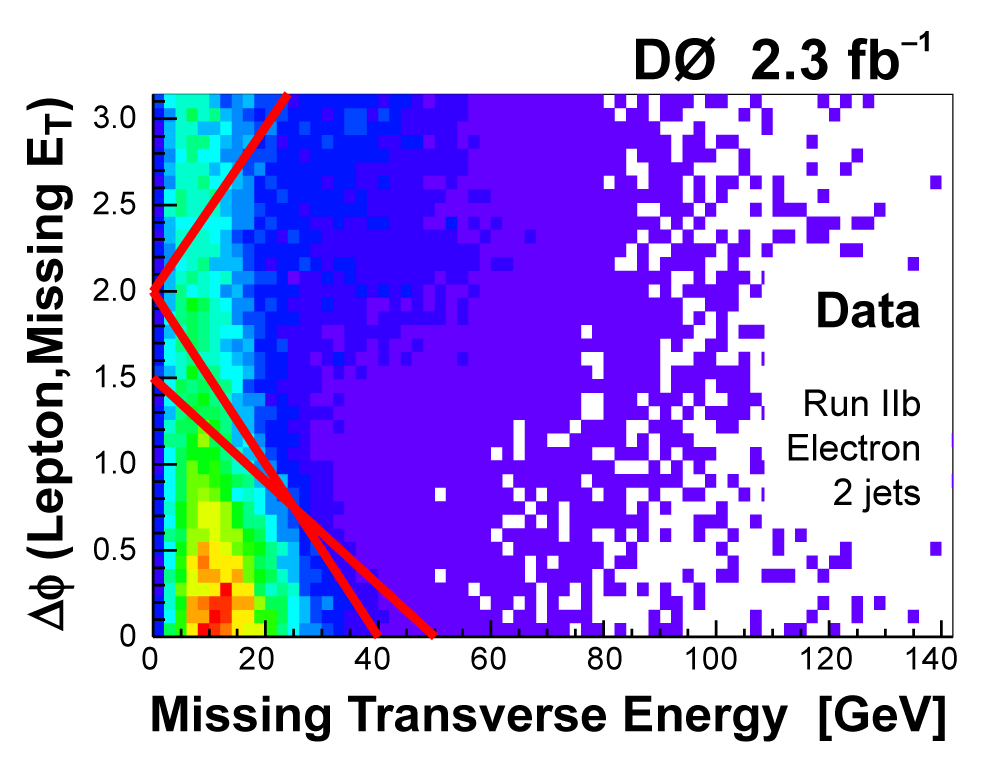
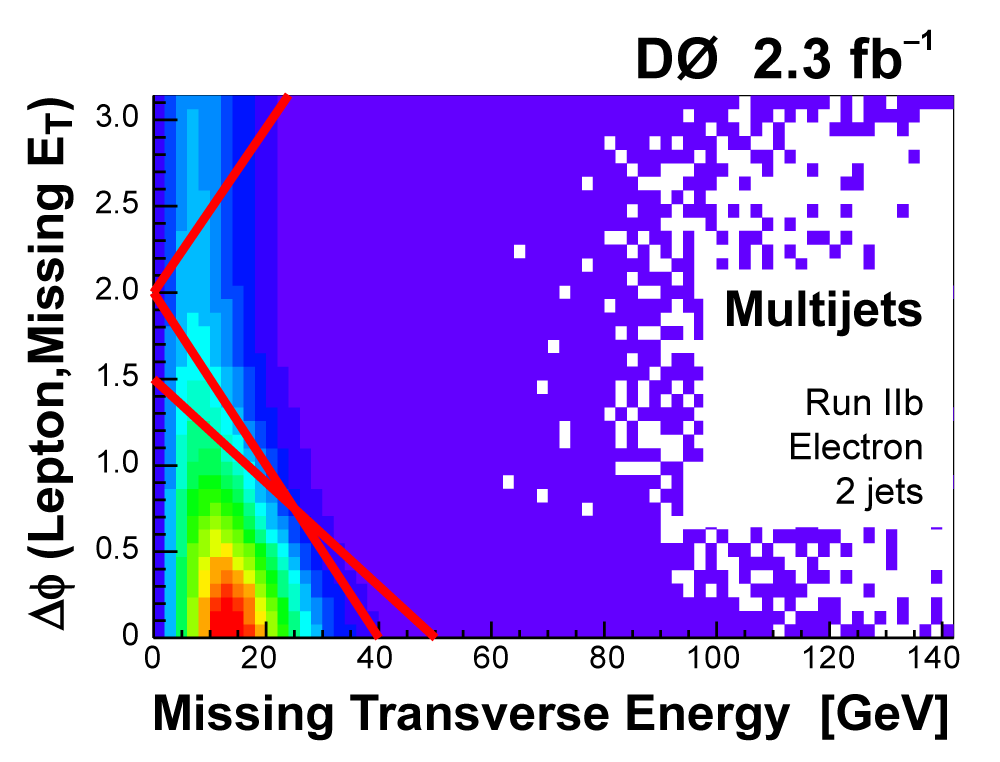
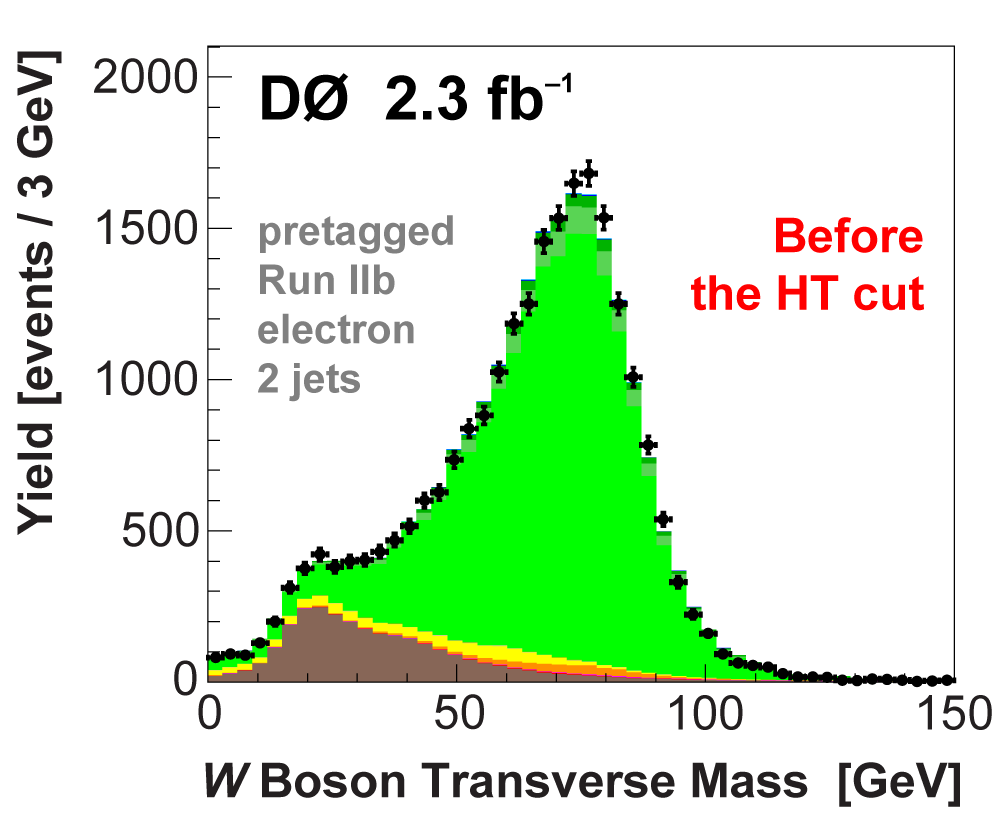
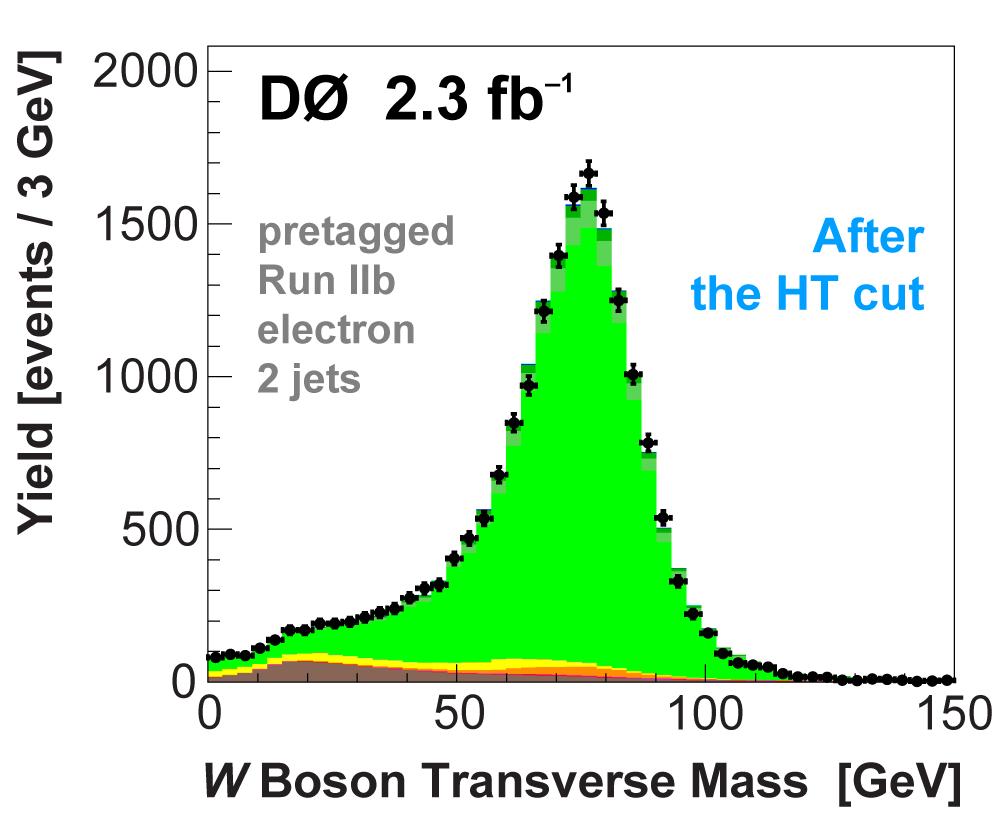
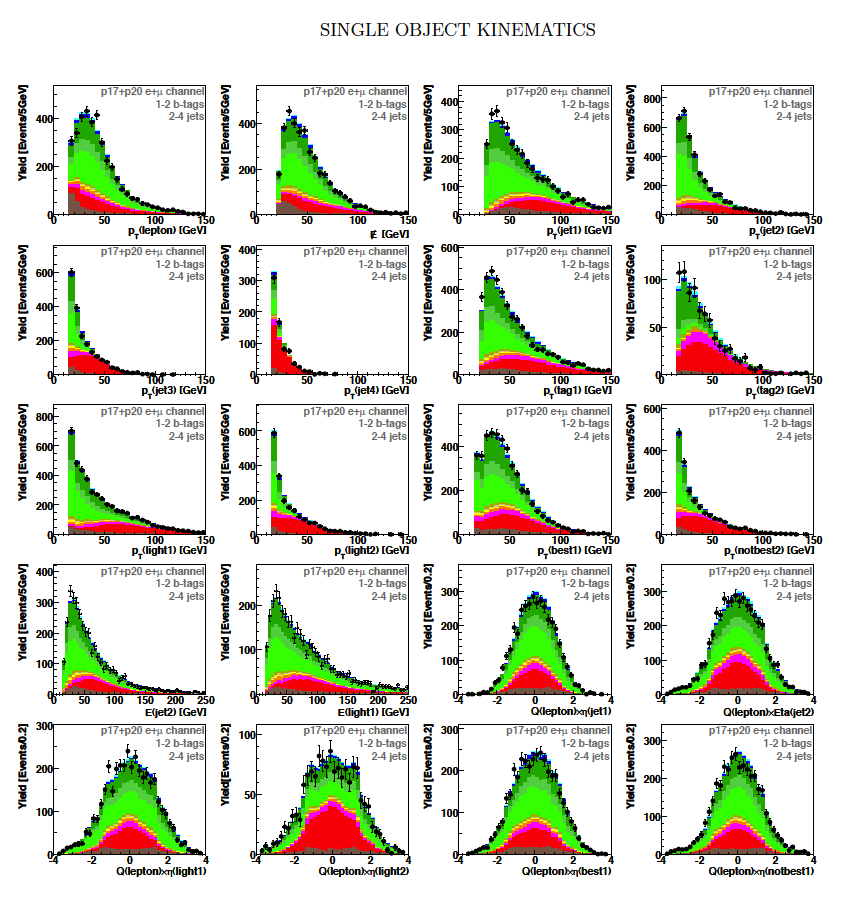
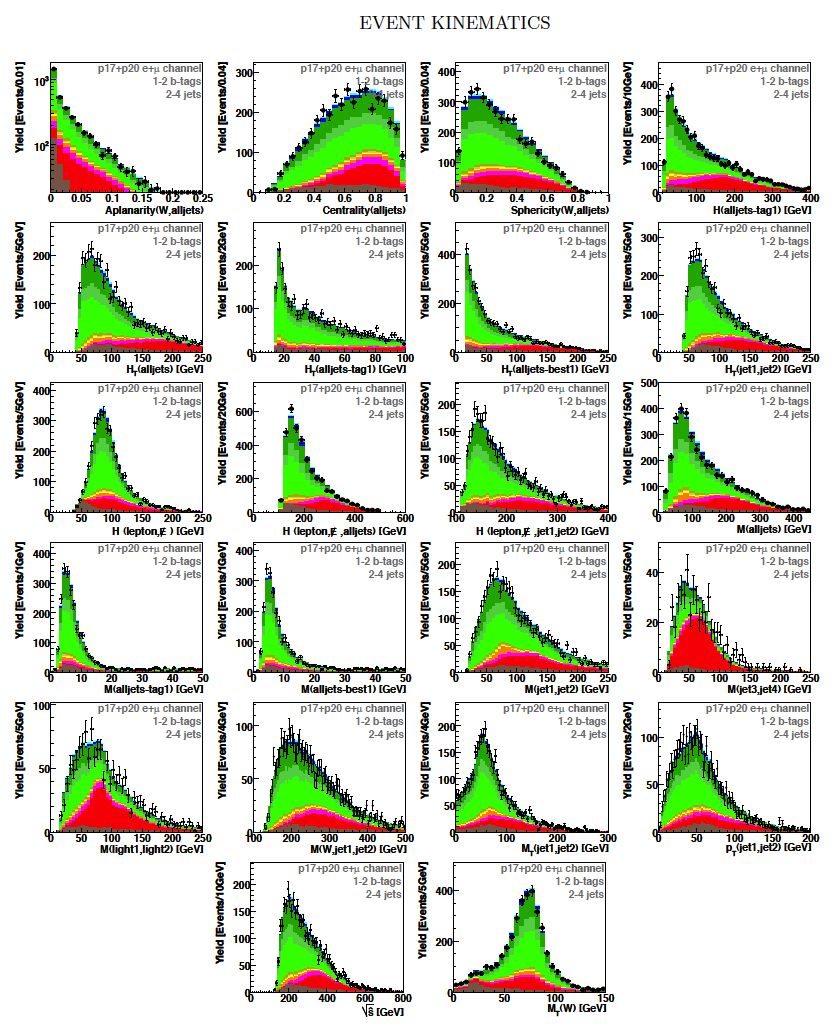
| We perform the analysis in 24 independent analysis channels (Run IIa, Run IIb; electron, muon; 2,3,4 jets; 1,2 b-tags) to take advantage of the different signal:background ratios and dominant sources of background. In additional to checking the distributions of about 160 variables for data-background agreement in all analysis channels separately, before and after b-tagging , we also define two cross-check samples to check the background model components separately. The first sample has low total energy (exactly two jets and the total transverse energy HT(lepton,neutrino,alljets) < 175 GeV), and only one b-tagged jet, to maximize the W+jets content and minimize the top pairs contribution, and the second sample has high total energy (exactly four jets and HT > 300 GeV), and one or two b-tagged jets, to maximize the top pairs component and minimize the W+jets contribution. We find good agreement for both normalization and shape in all variables studied. The W boson transverse mass distribution is shown here as an example. |
 |
 |
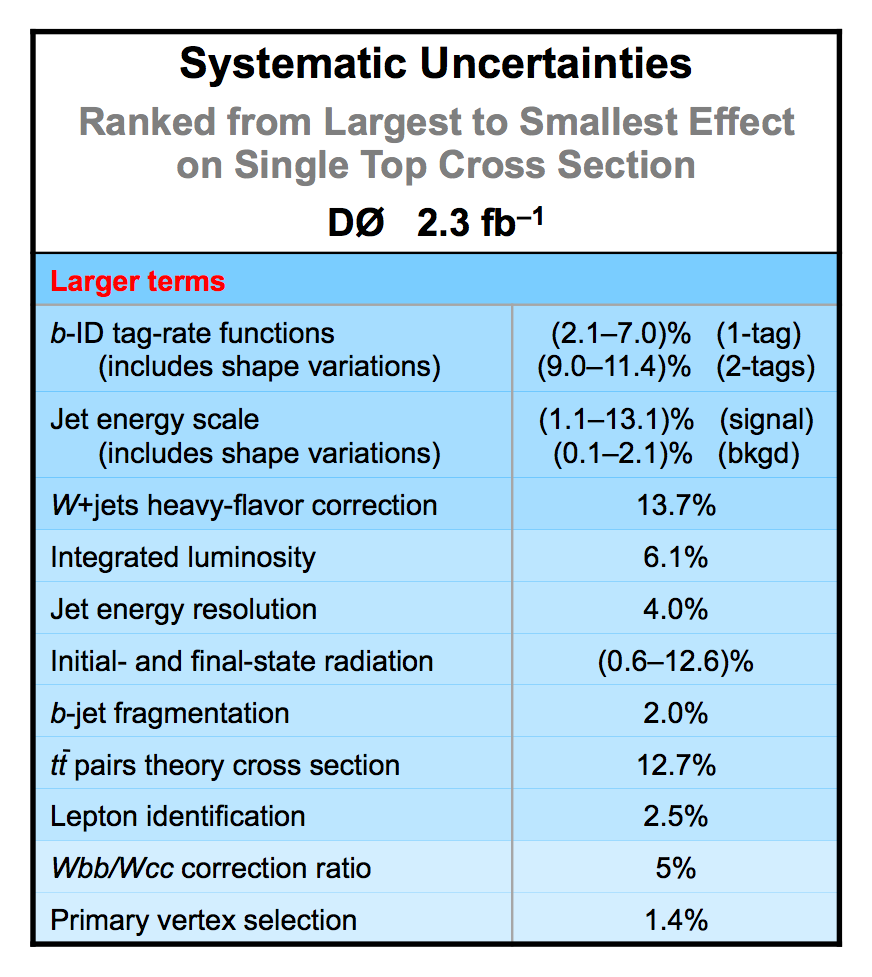
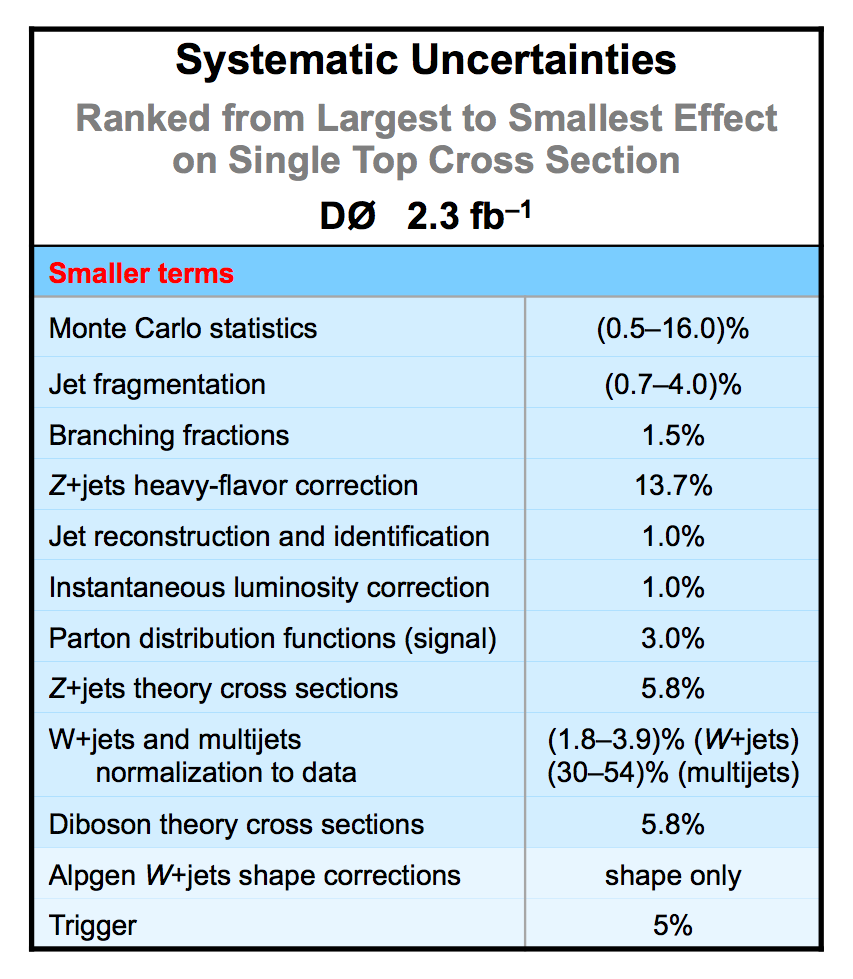
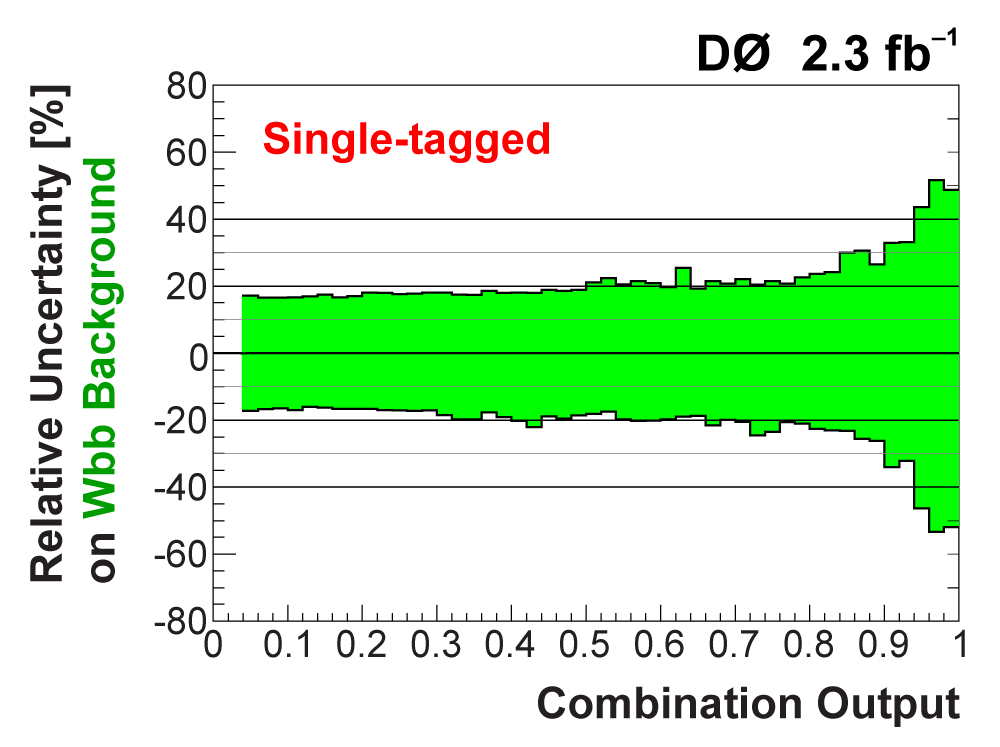
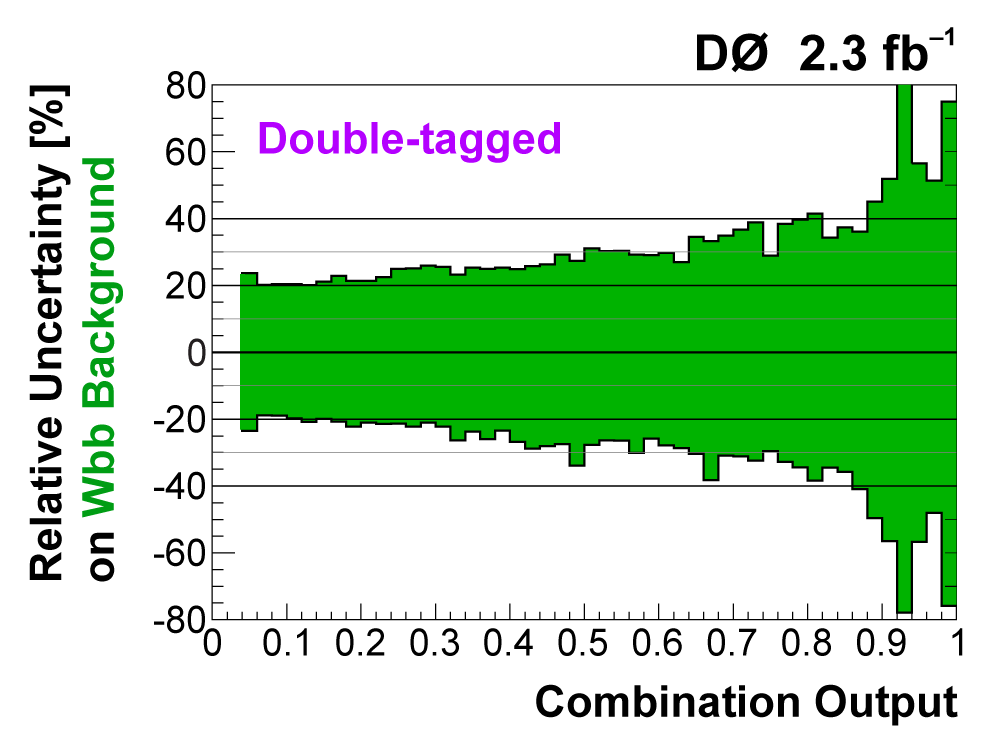
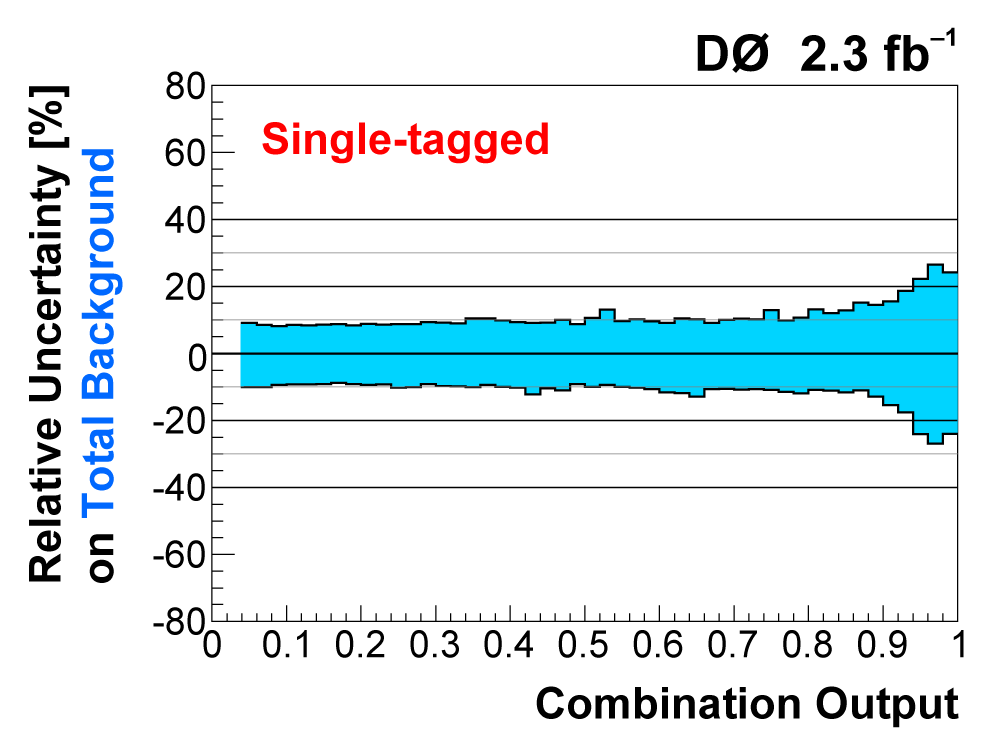
| The uncertainties in all searches are dominated by the statistical uncertainty from the size of the data sample. However, once there is enough data to observe and measure something, then systematic contributions to the total uncertainty become important. The total uncertainty on the single top cross section measured in this observation analysis is ±22%. When we perform the calculation without including any systematics, it is 18% (i.e., this is the statistical uncertainty). Thus, the systematic component of the total cross section is approximately 13%. We consider both normalization systematic uncertainties and shape-dependent systematic uncertainties separately for each signal and background source in each analysis channel. The overall background uncertainty varies between 7% and 15% for the individual channels. Shape uncertainties result in 20% to 40% uncertainties in the discriminant output region near one. The following two tables show the sources of systematic uncertainty included in this measurement, in ranked order of contribution to the total cross section uncertainty. Other potential sources of systematic uncertainty were studied and found to have a negligible effect. |
 |
 |
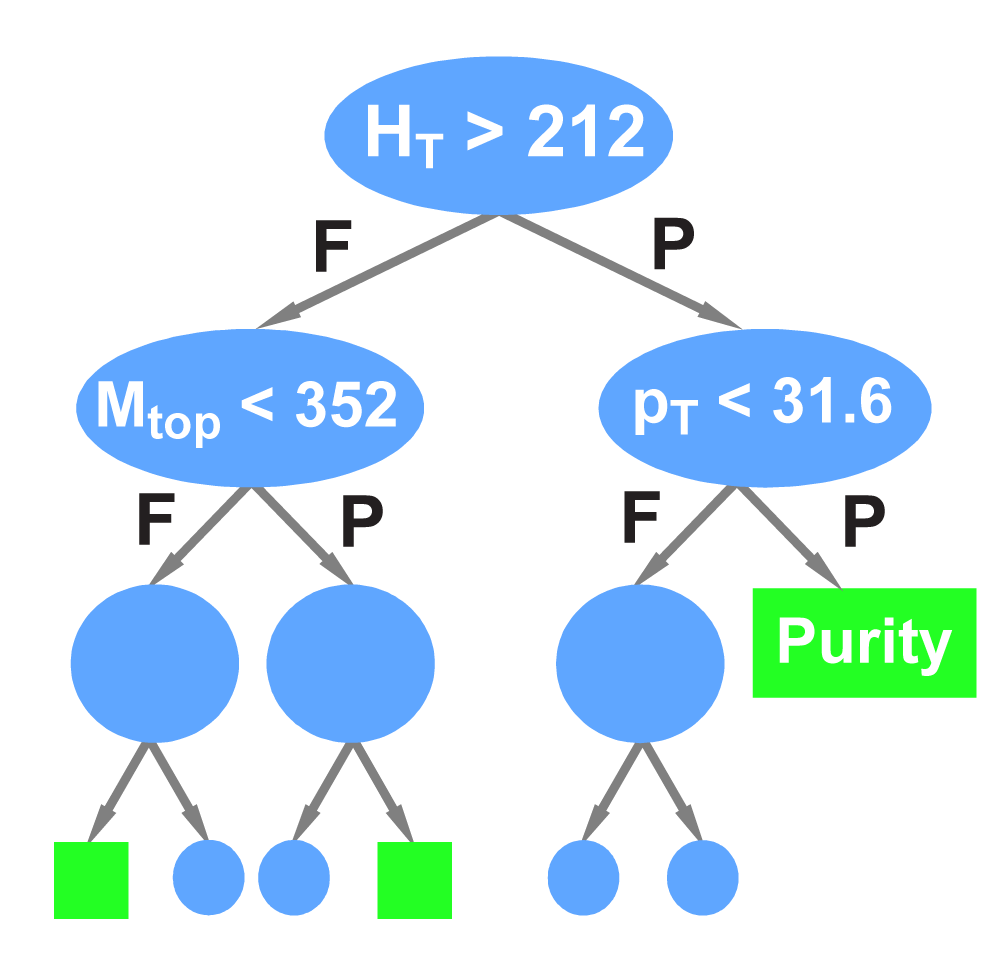
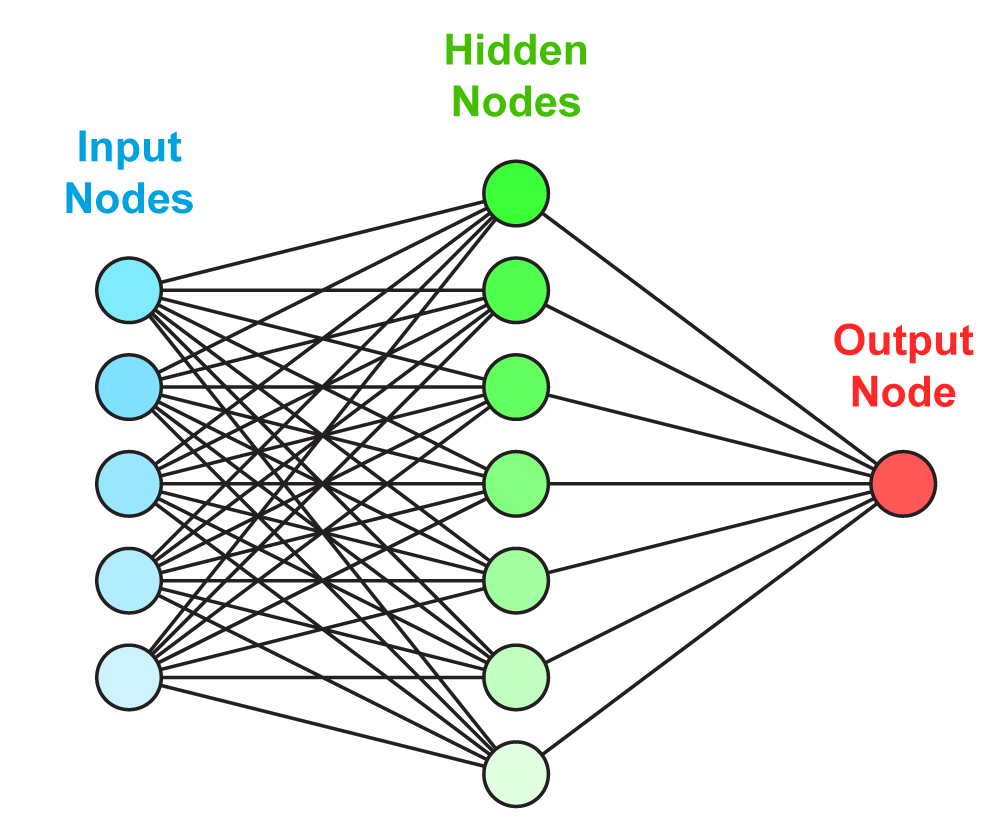
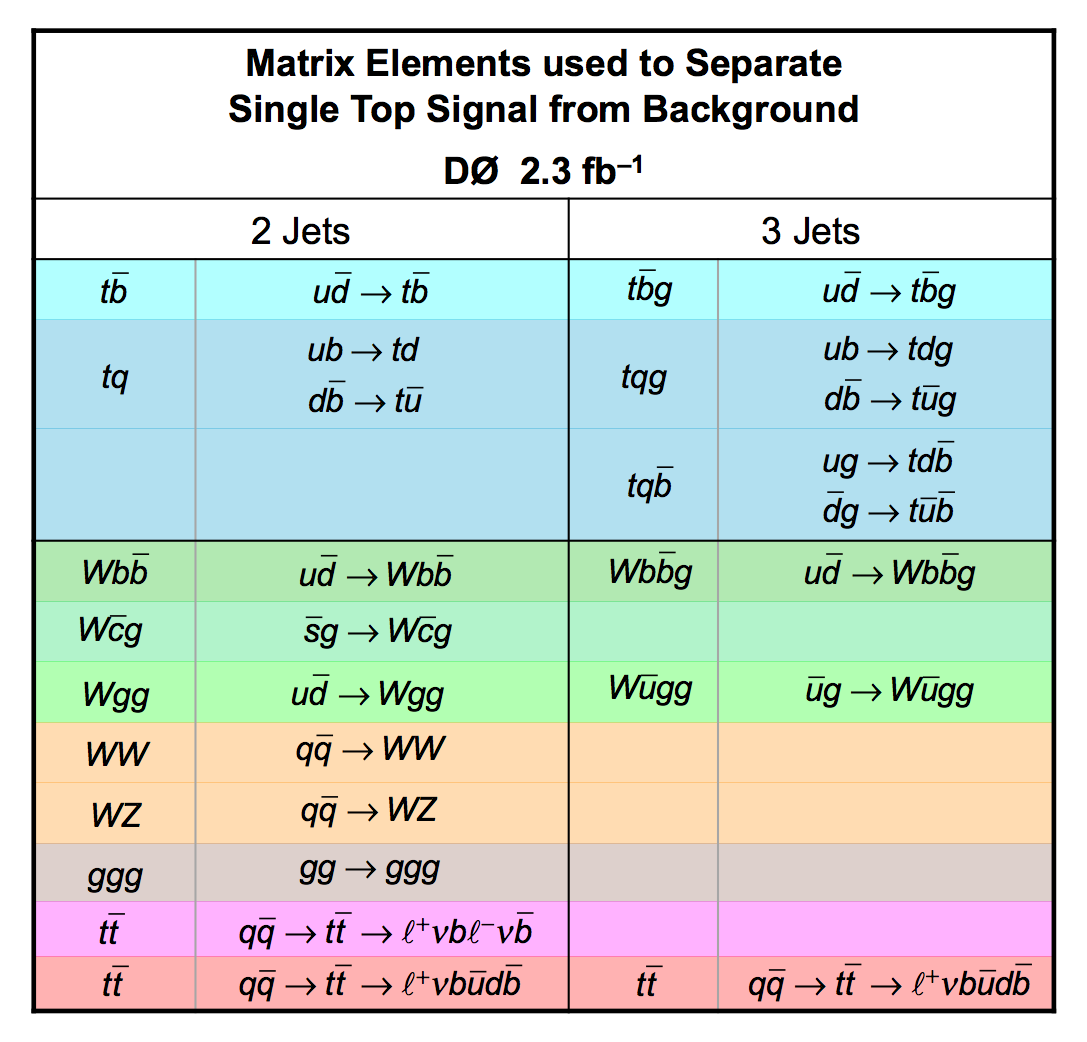
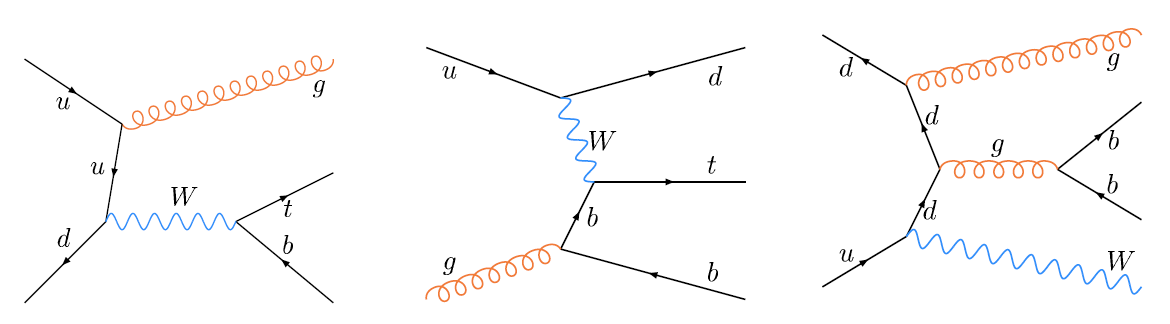
We apply three methods to separate signal from background:
|
 |
 |
 |
 |
 |
 |
 |
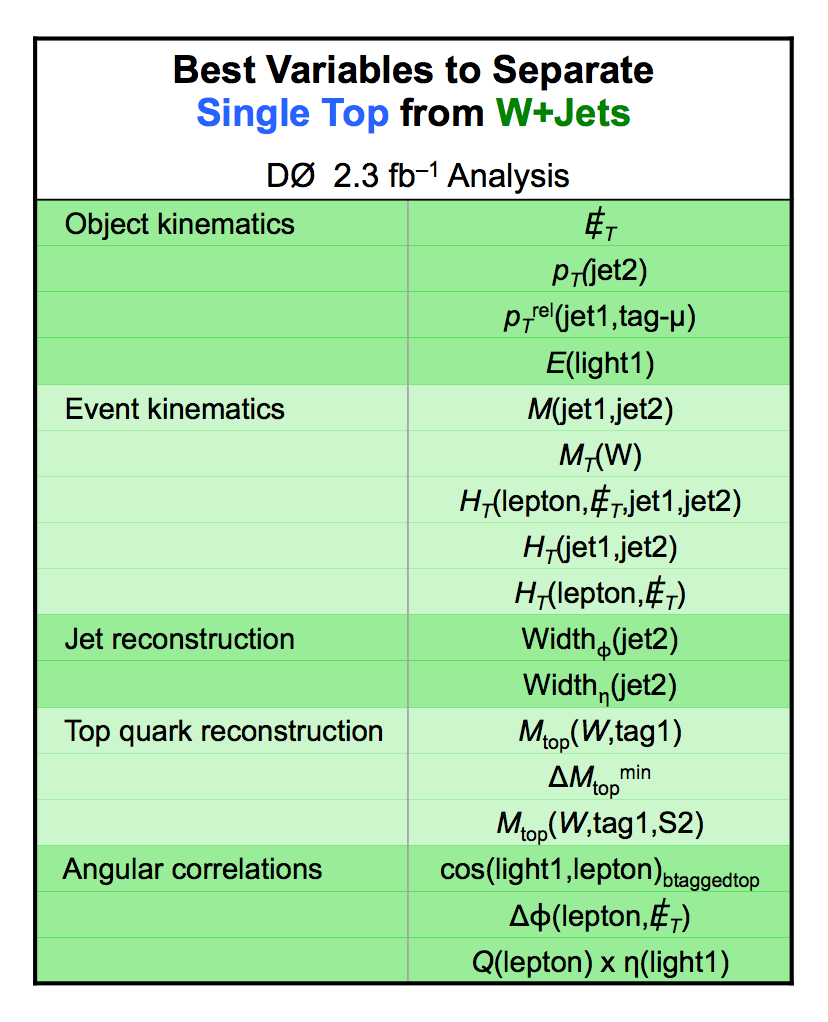
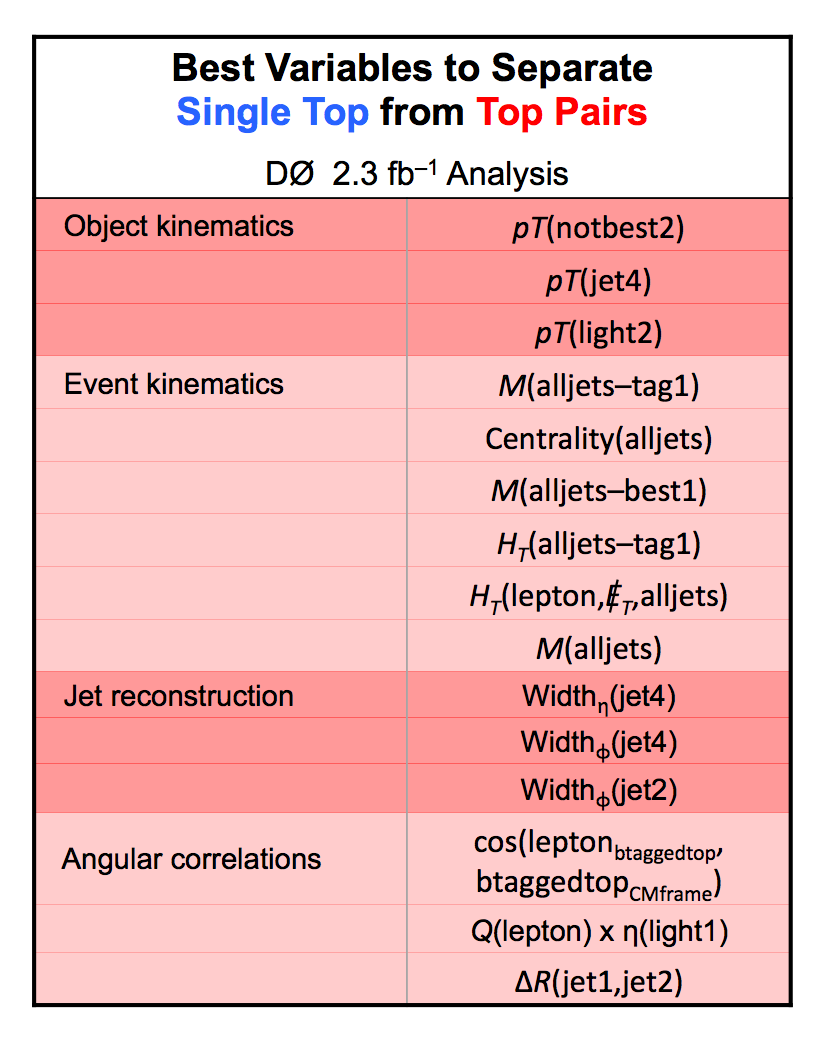
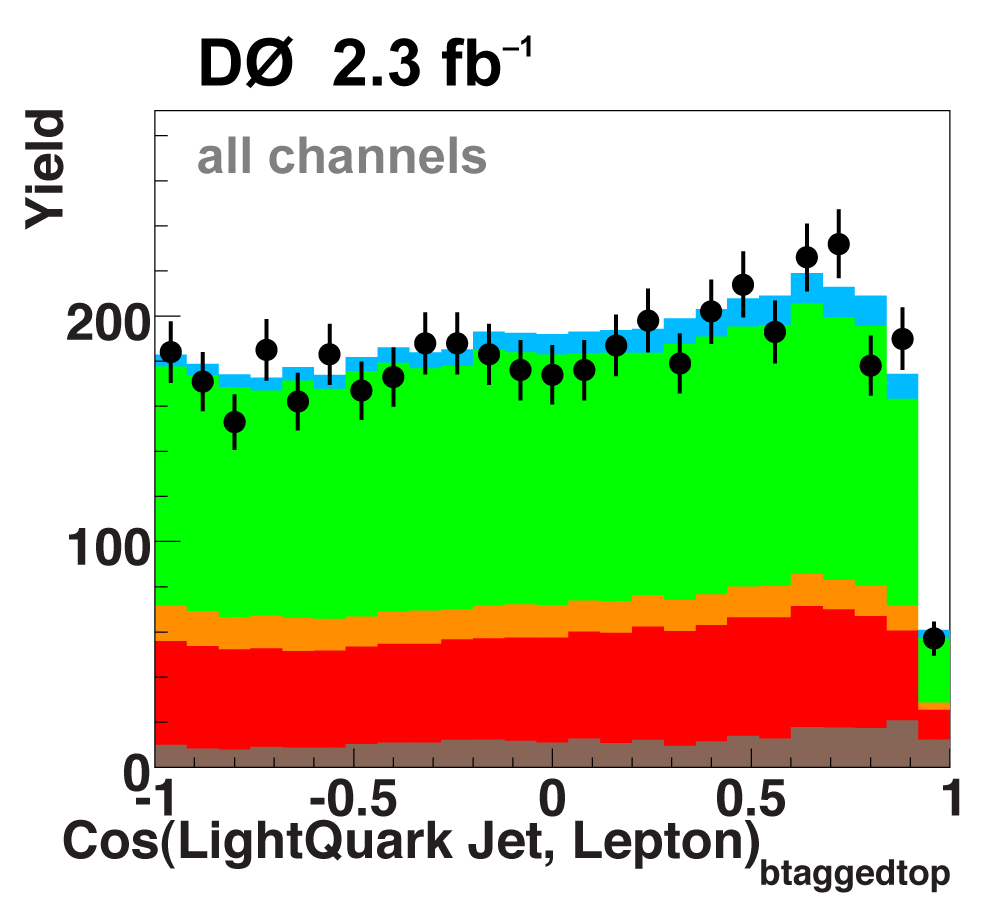
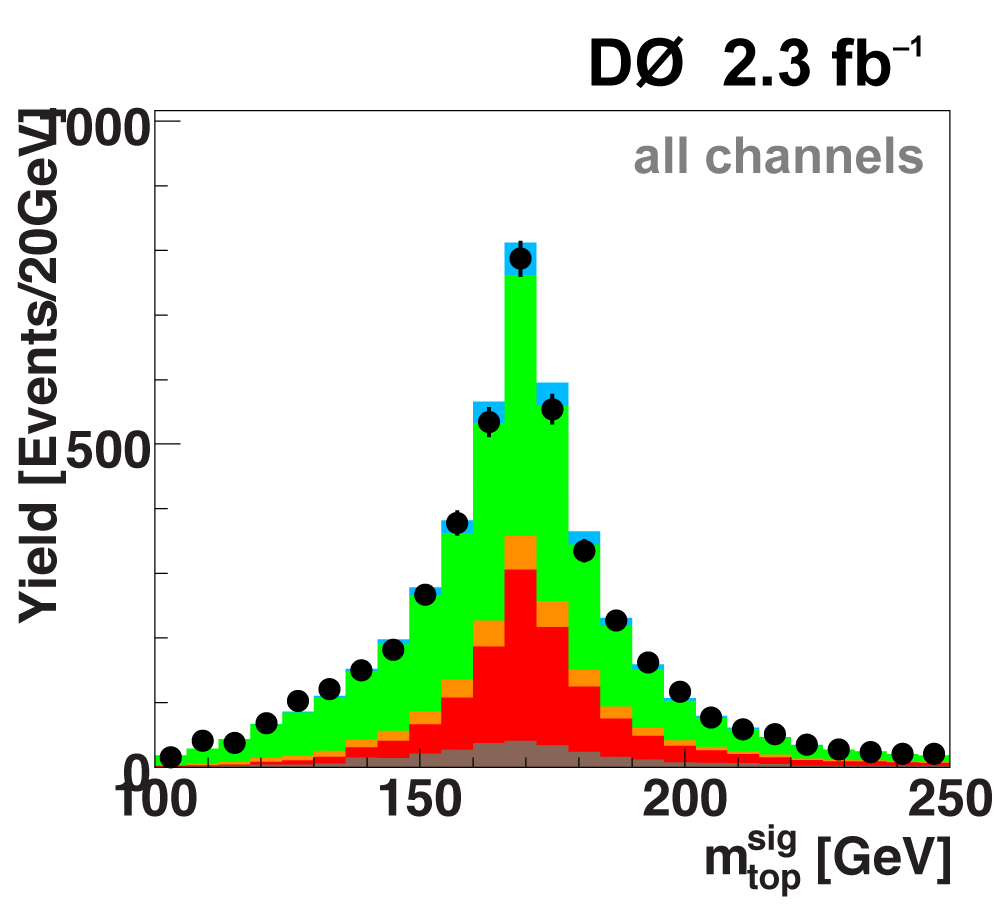
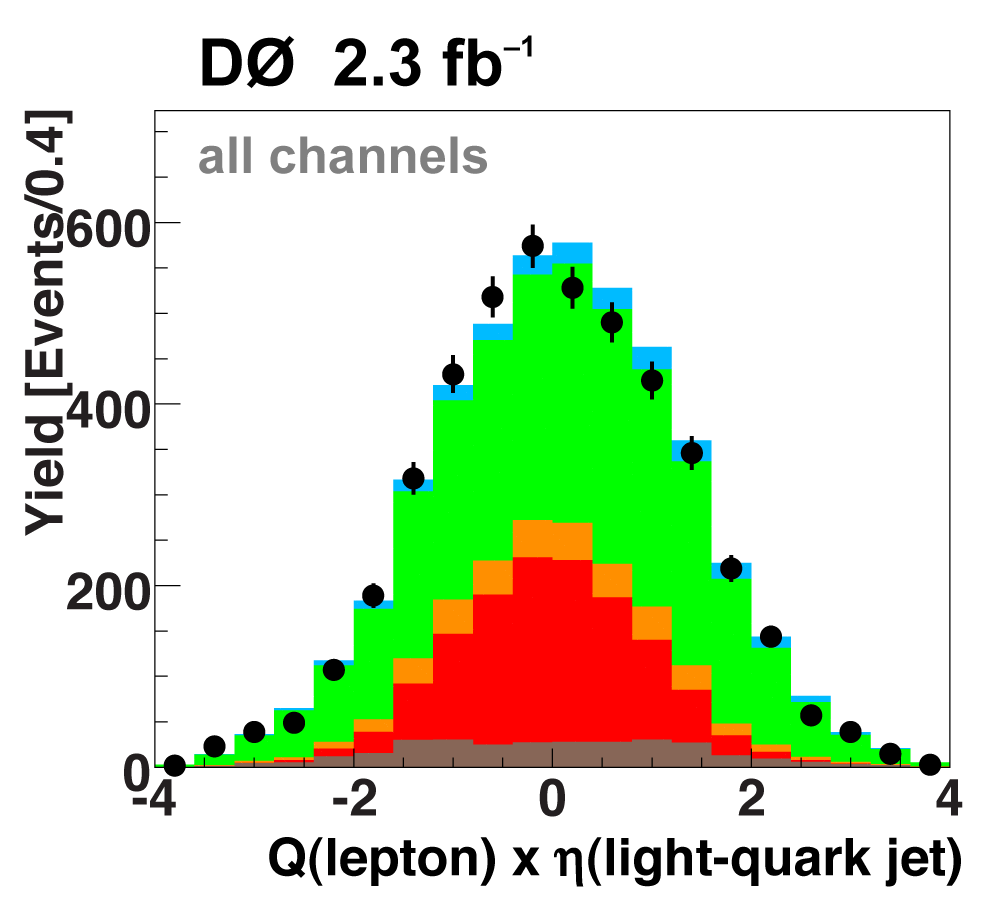
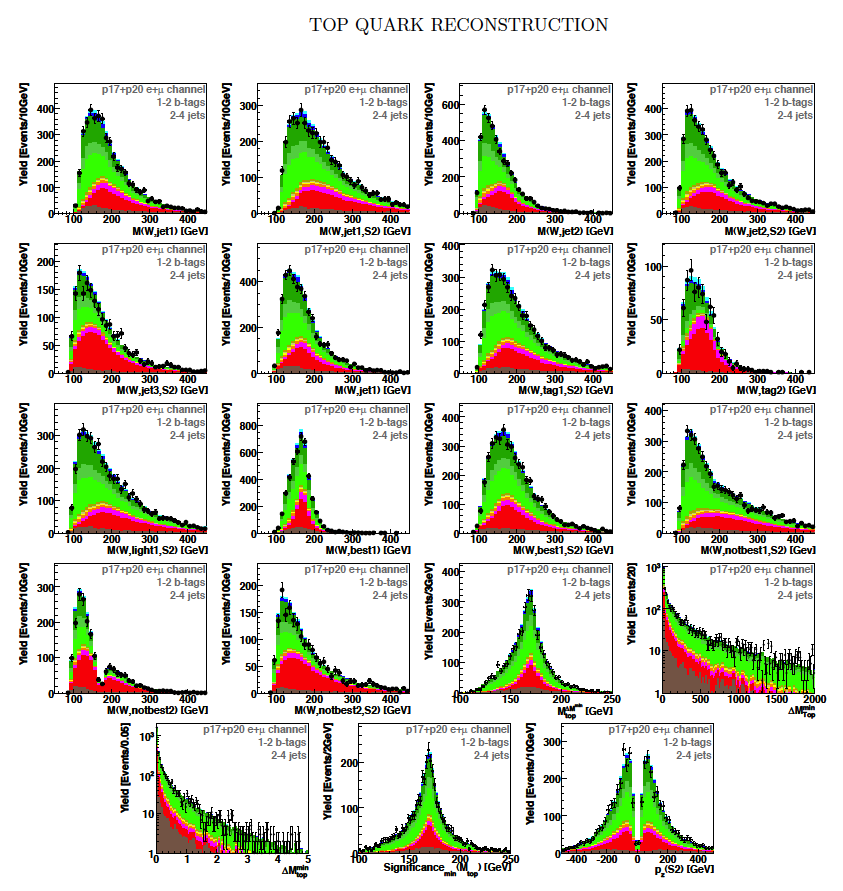
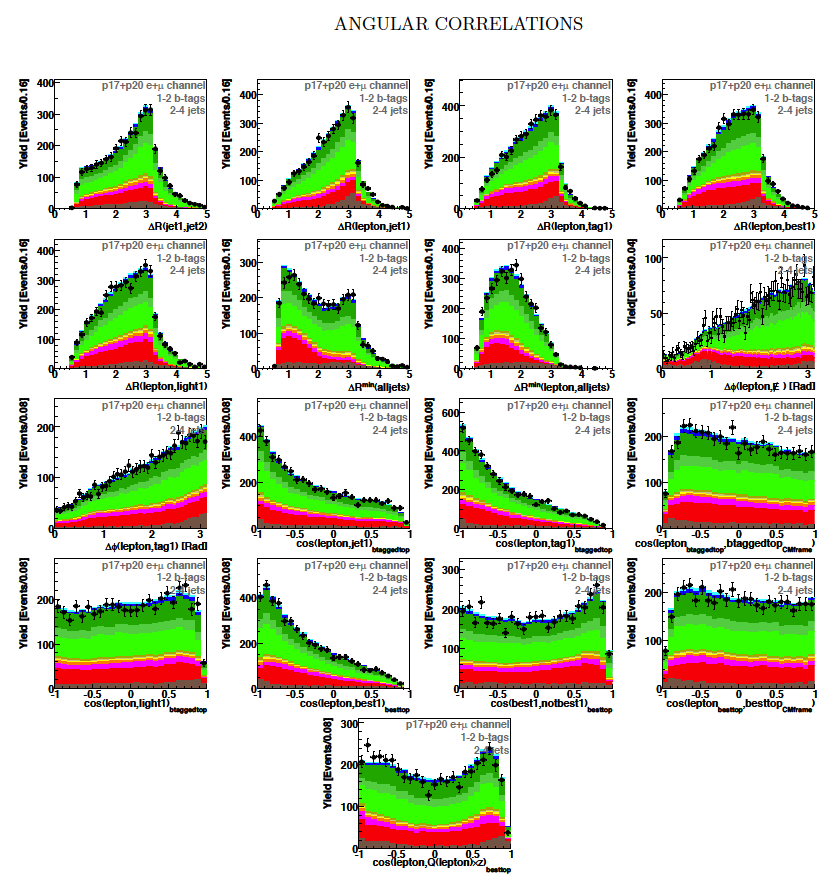
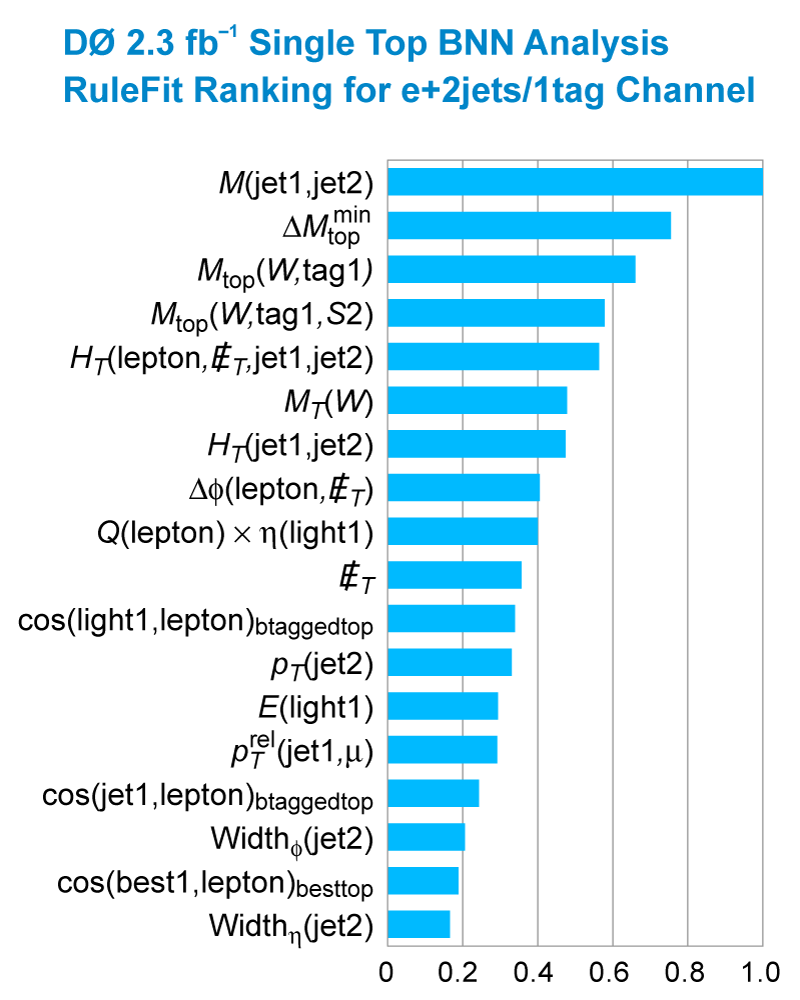
| These tables show the variables used by the boosted decision trees and the Bayesian neural networks. (Plots of all variables are at the bottom of the page.) Some comments on the notation are in order. The numbering n of jetn, tagn, lightn, etc. refers to the transverse momentum ordering of the jets, 1 is the highest pT jet of that type of jet, 2 is the second-highest pT jet, and so on. "tag" means a b-tagged jet. "light" means an untagged jet (it failed the b-tag criteria). "best" means the jet which, when combined with the lepton and missing transverse energy, produces a reconstructed top quark mass closest to 170 GeV (the value at which we did the analysis). "notbest" means any jet that is not the best jet. "alljets" means include all the jets in the event in the global variable (there are 2, 3, or 4 of them). pT is the transverse momentum. E is the particle energy. Q is the particle's charge. H is the scalar sum of the particles' energies. HT is the scalar sum of the transverse energies. M is the invariant mass of the objects. MT is the transverse mass of the objects. Sqrt(s^hat) is the total center of mass energy in the event. pTrel is the transverse momentum of the muon relative to the closest jet. S1 and S2 are the two solutions for the neutrino longitudinal momentum when solving the W boson mass equation, and S1 is the smallest absolute value of the two (the preferred value). MtopΔMmin is the reconstructed top quark mass using the jet and neutrino solution that make the mass closest to 170 GeV. ΔMtopmin is the difference in GeV between MtopΔMmin and 170 GeV. Mtopsig is the reconstructed top quark mass using the jet and neutrino solution that gives the lowest value for "significance," where Significancemin(Mtop) is loge of the jet and missing transverse energy resolution functions calculated at Mtop divided by the resolution functions at 170 GeV. ΔR is sqrt(Δφ2 + Δη2). |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
| All raw discriminant output distributions undergo a monotonic transformation of the binning to ensure that every bin (50 in each distribution) has at least 40 background events, so that there are no bins with a nonzero signal prediction or data but not enough background in the model to use that information. The bins from the matrix elements outputs are then also reordered in descending signal:background ratio from 1 towards 0. After transformation, analysis channels with lower statistics do not have entries in all 50 bins, the filled bins start at one and end before reaching zero. The following plots illustrate the output transformation process for one channel in the boosted decision trees analysis. |
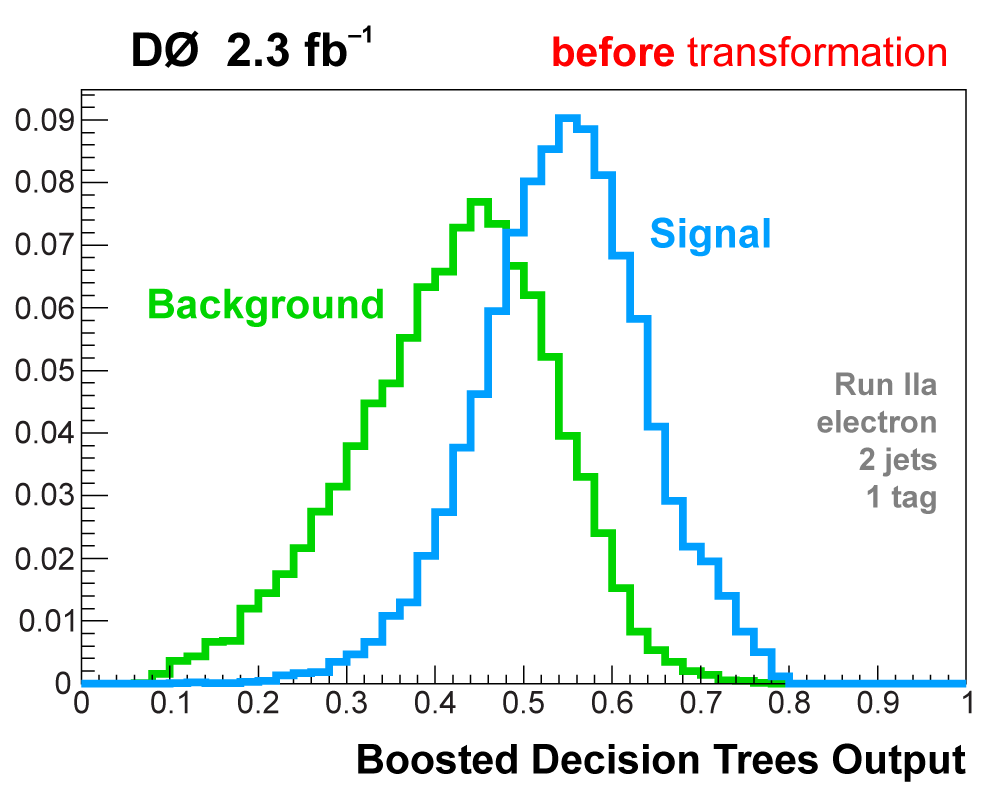 |
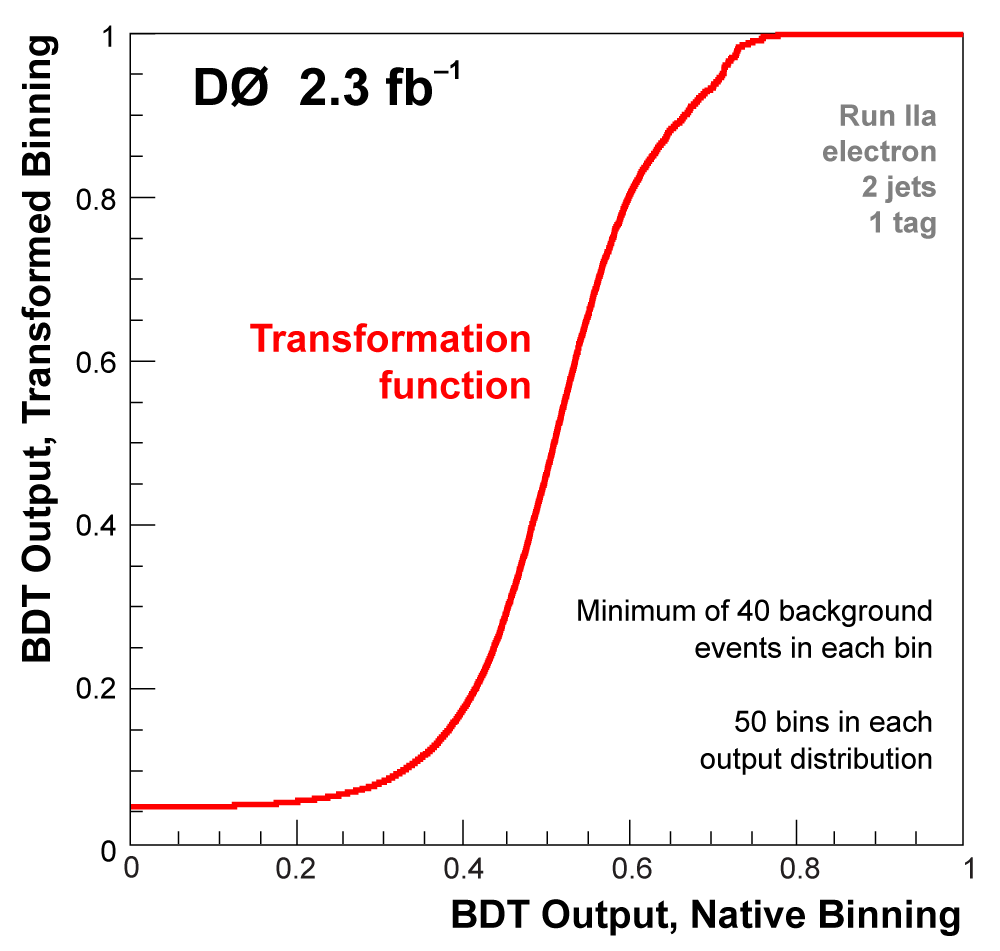 |
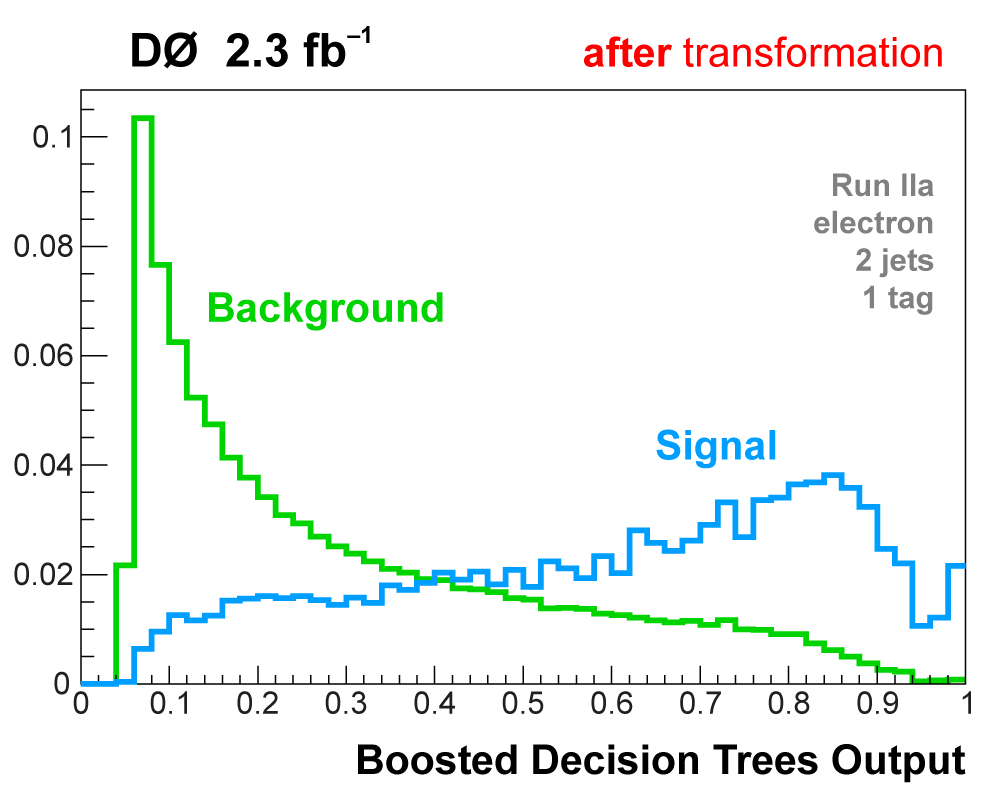 |
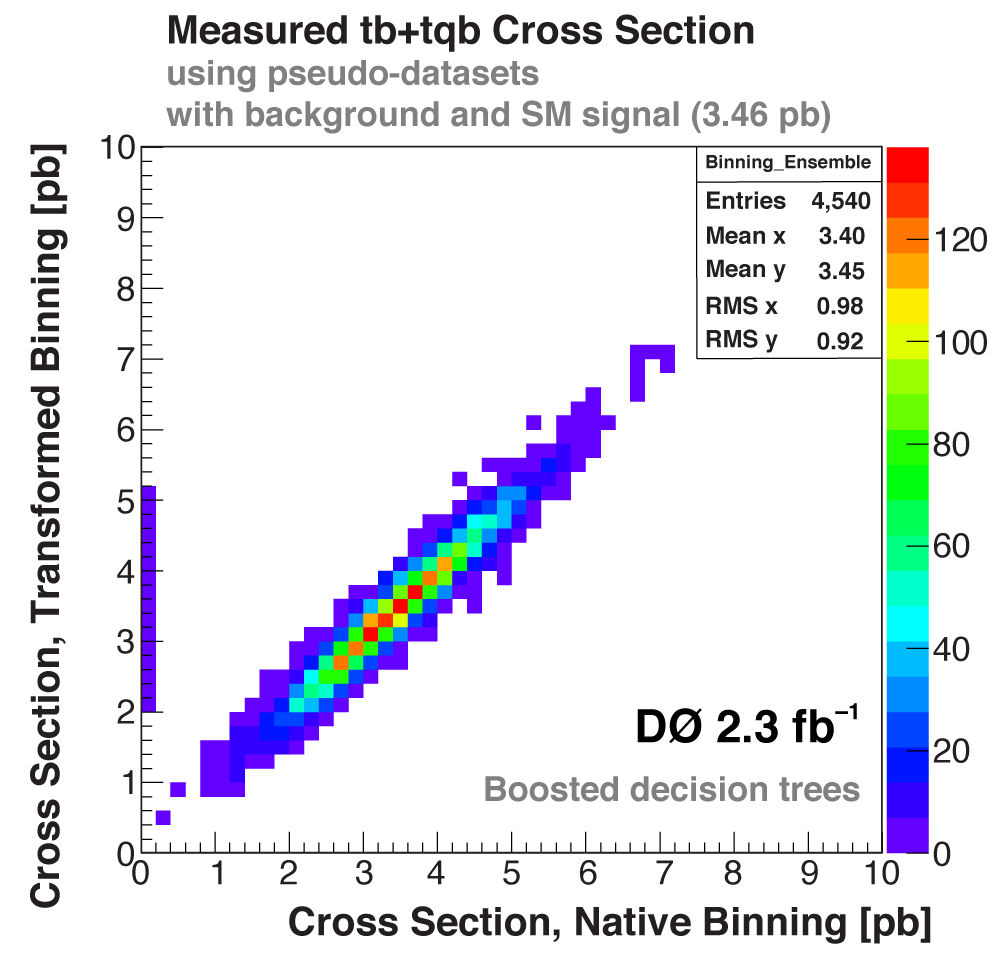 |
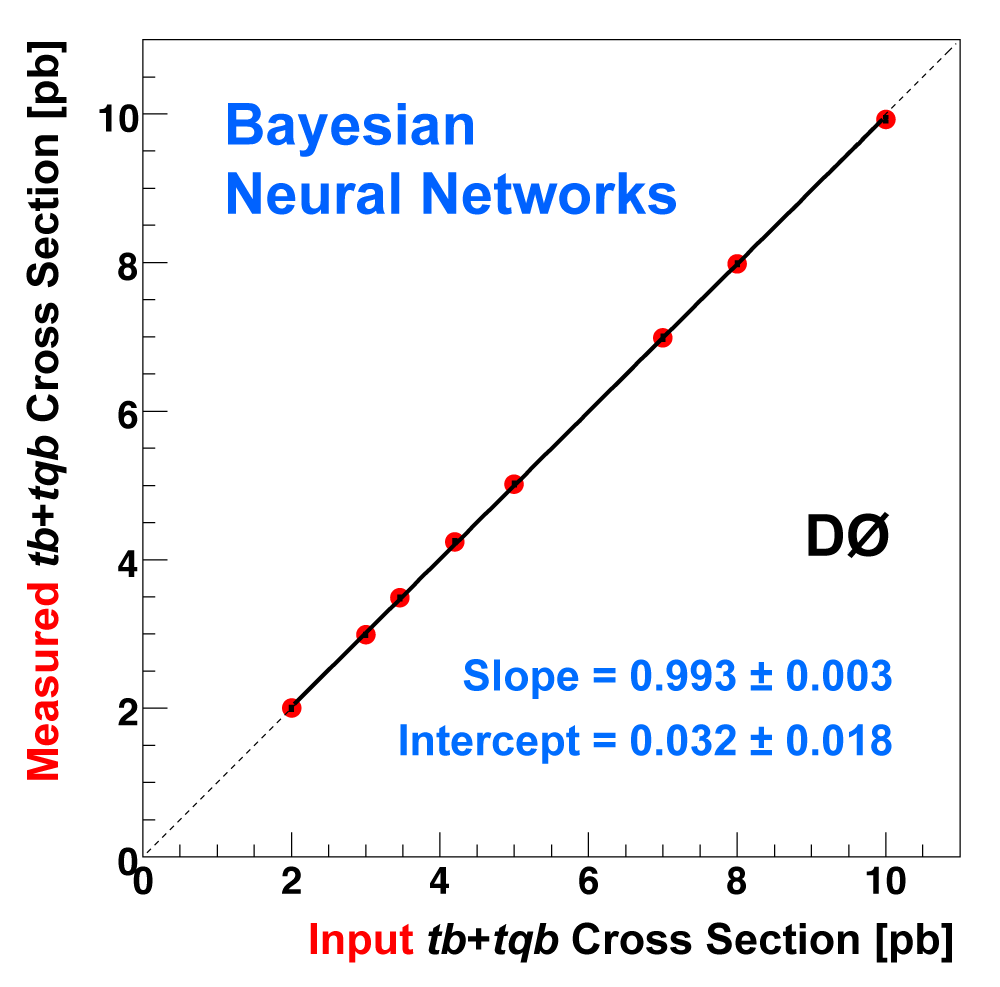
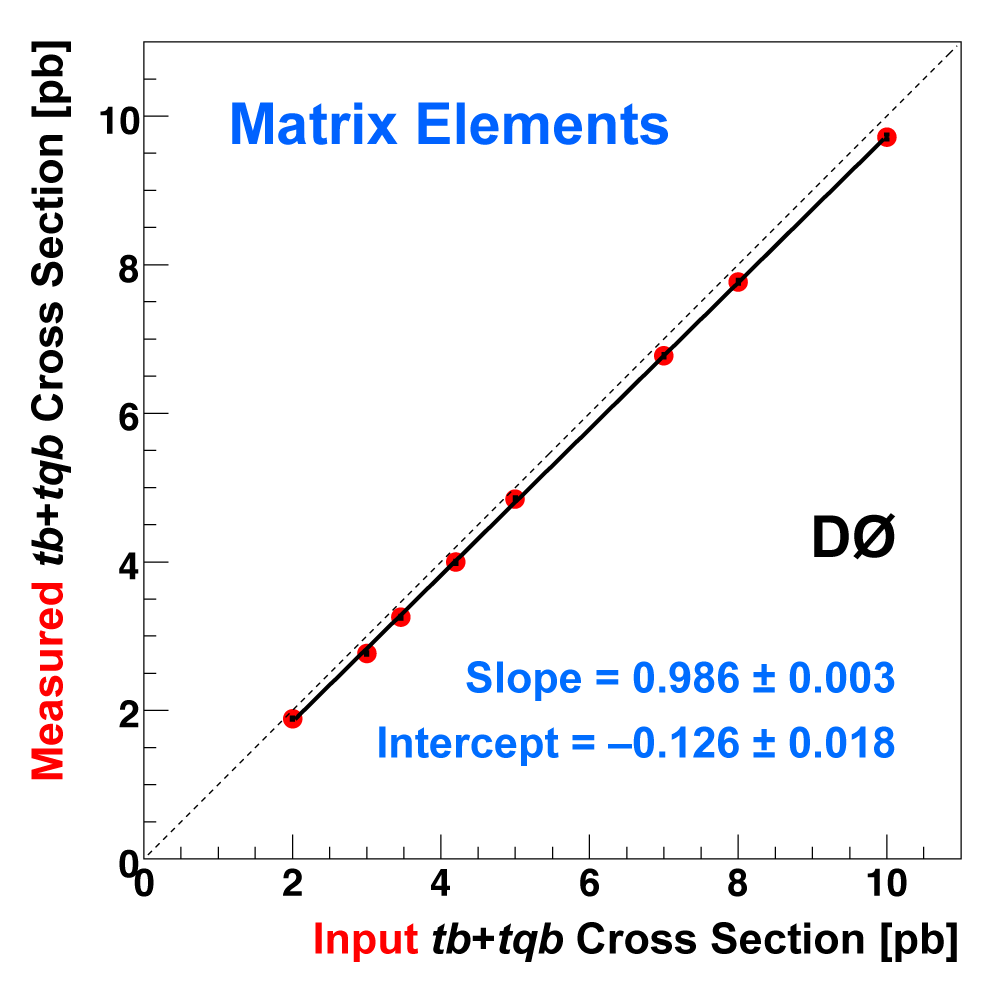
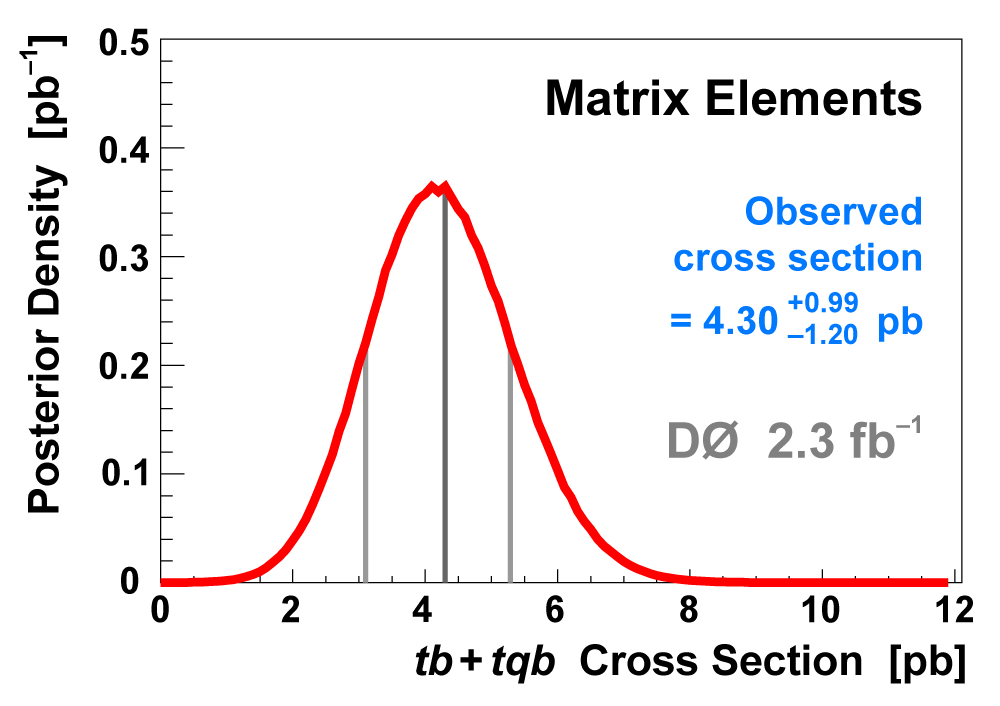
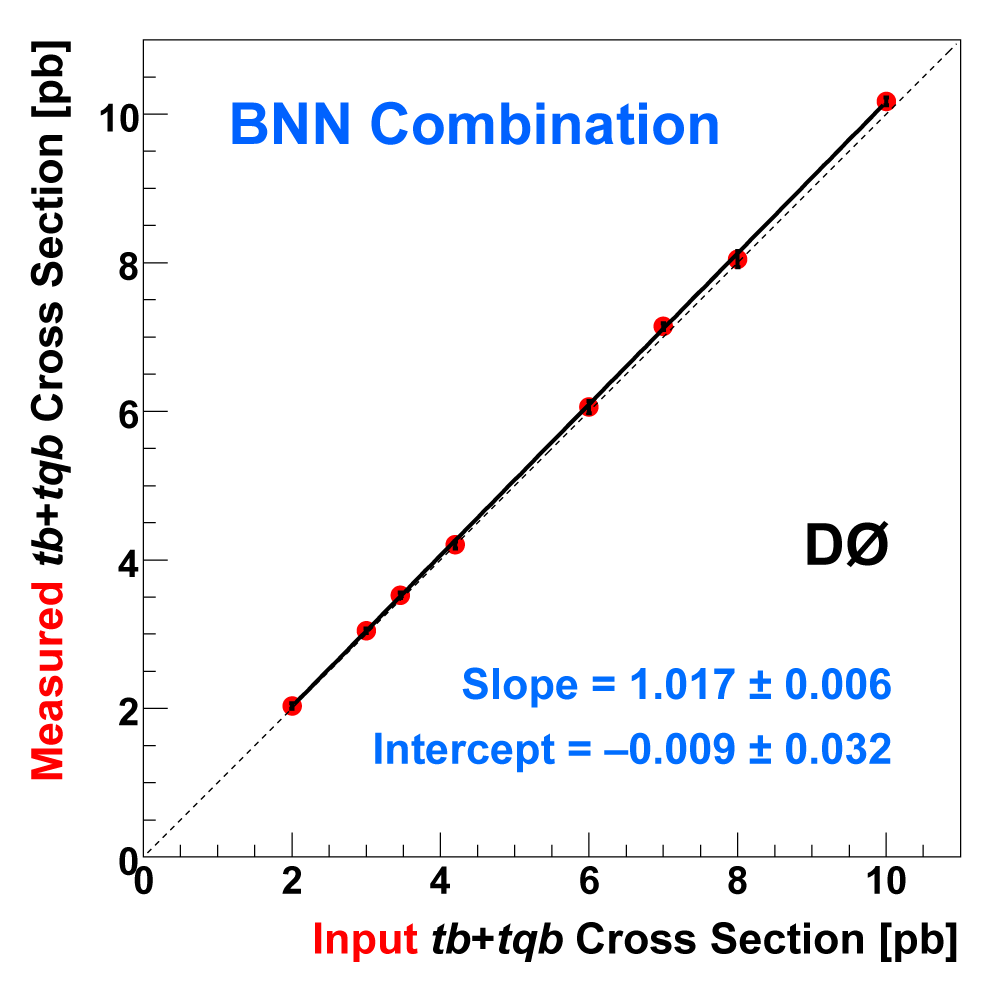
| The following three plots on the right show that each of the discriminant methods is able to accurately measure the single top cross section. These plots were produced using eight ensembles of pseudo-data. Each pseudo-dataset contains signal and background events and their uncertainties that model the real 2.3 fb-1 dataset. Each ensemble contains thousands of pseudo-datasets. The difference between the samples is the cross section value chosen for the single top events. This input cross section is reproduced by each discriminant analysis, as illustrated in the left-hand plot for the boosted decision tree discriminants and the ensemble with SM signal cross section. |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
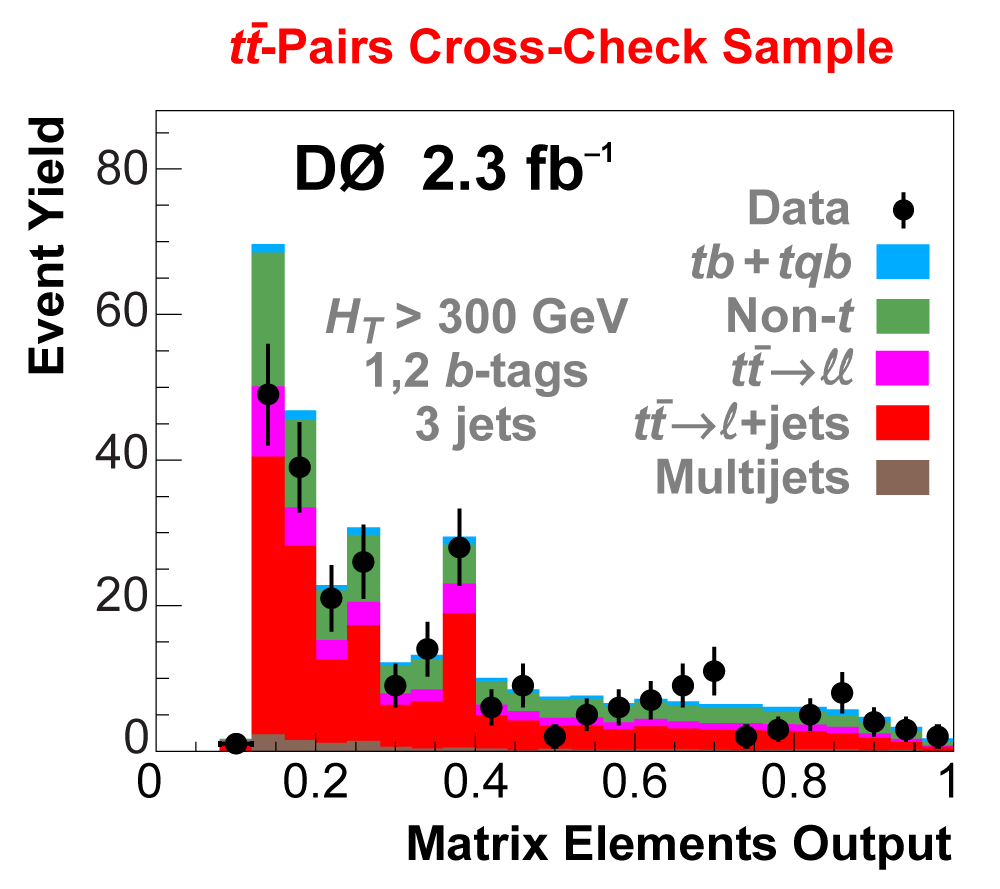 |
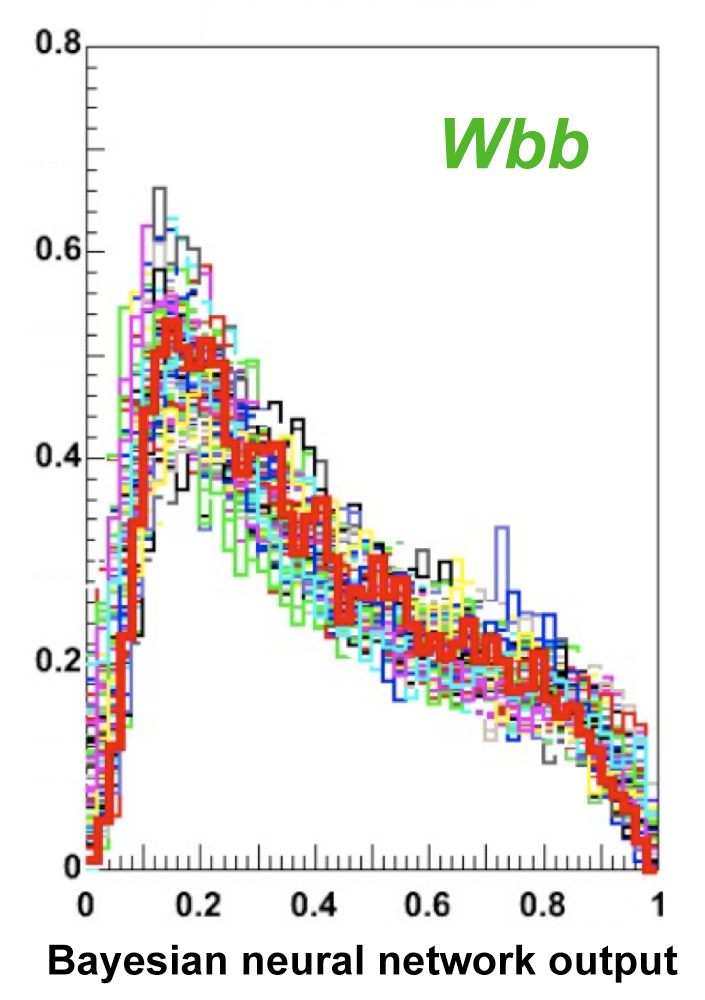
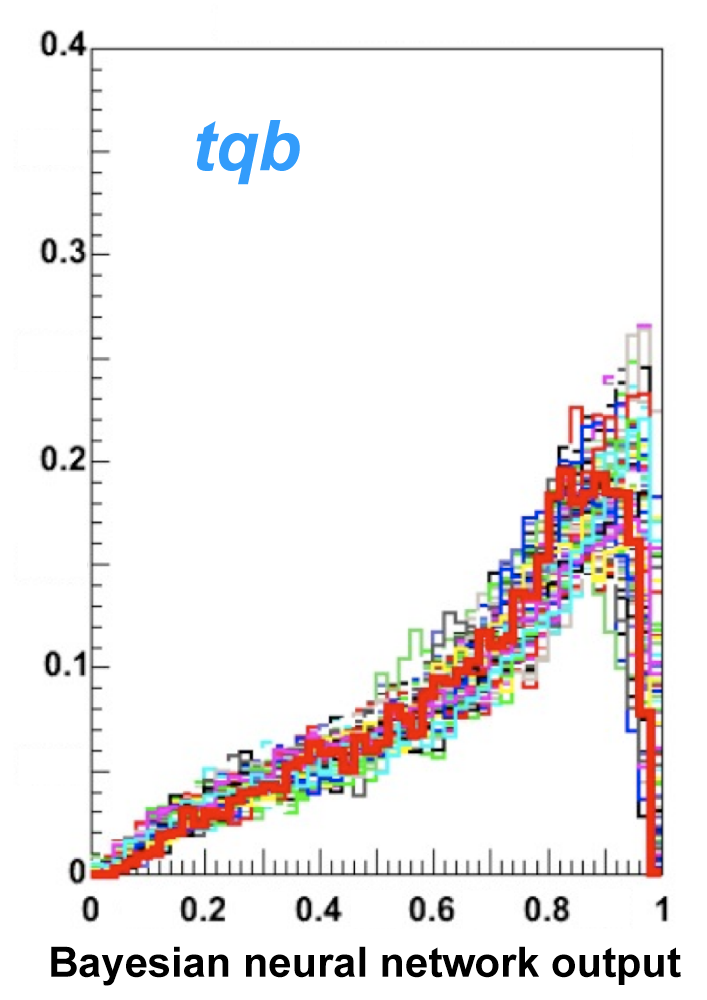
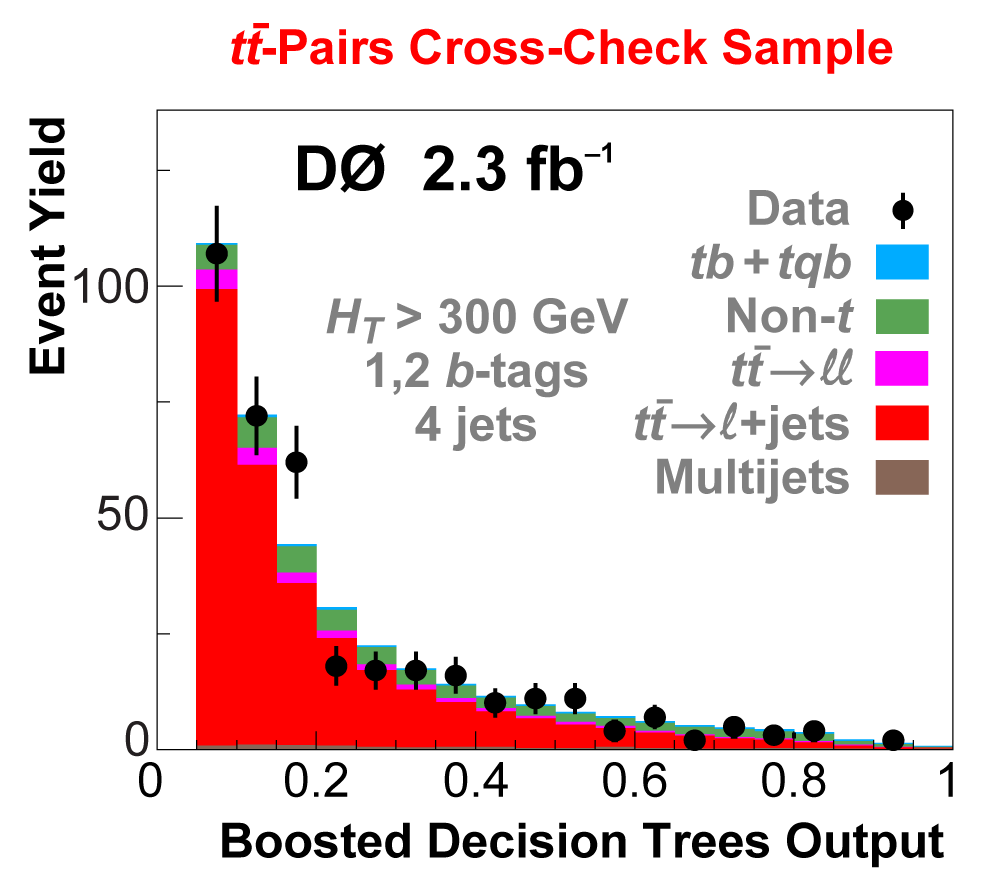
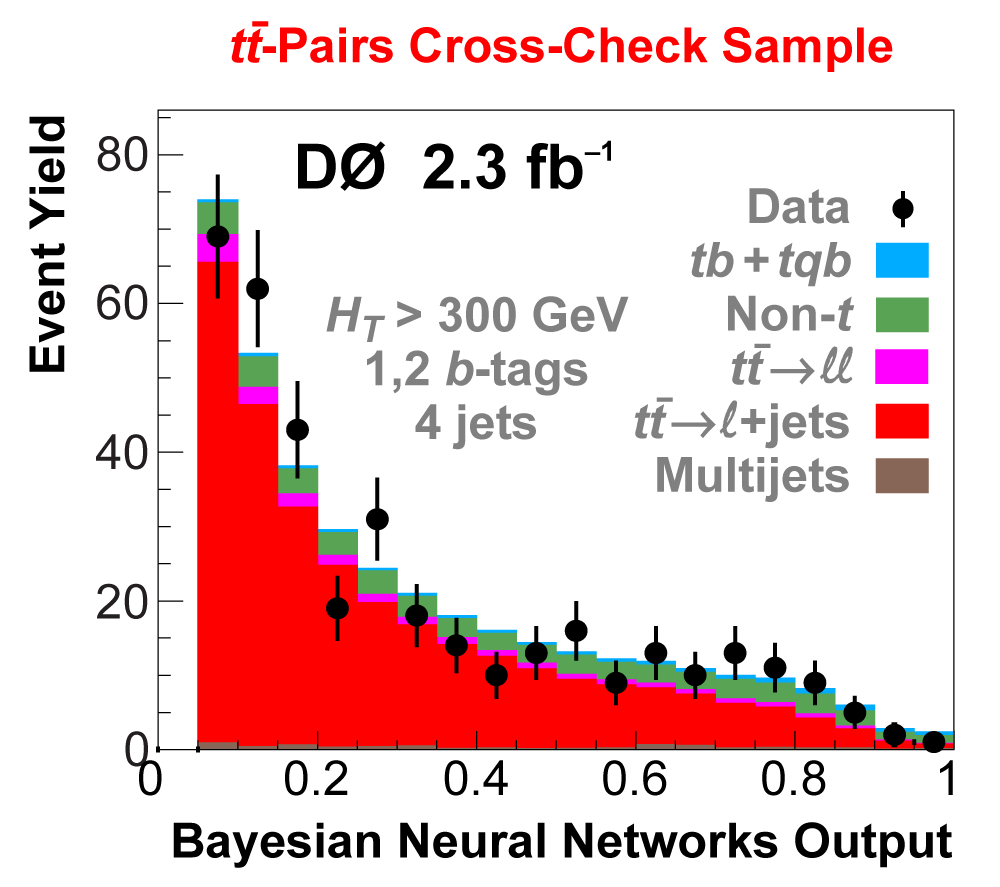
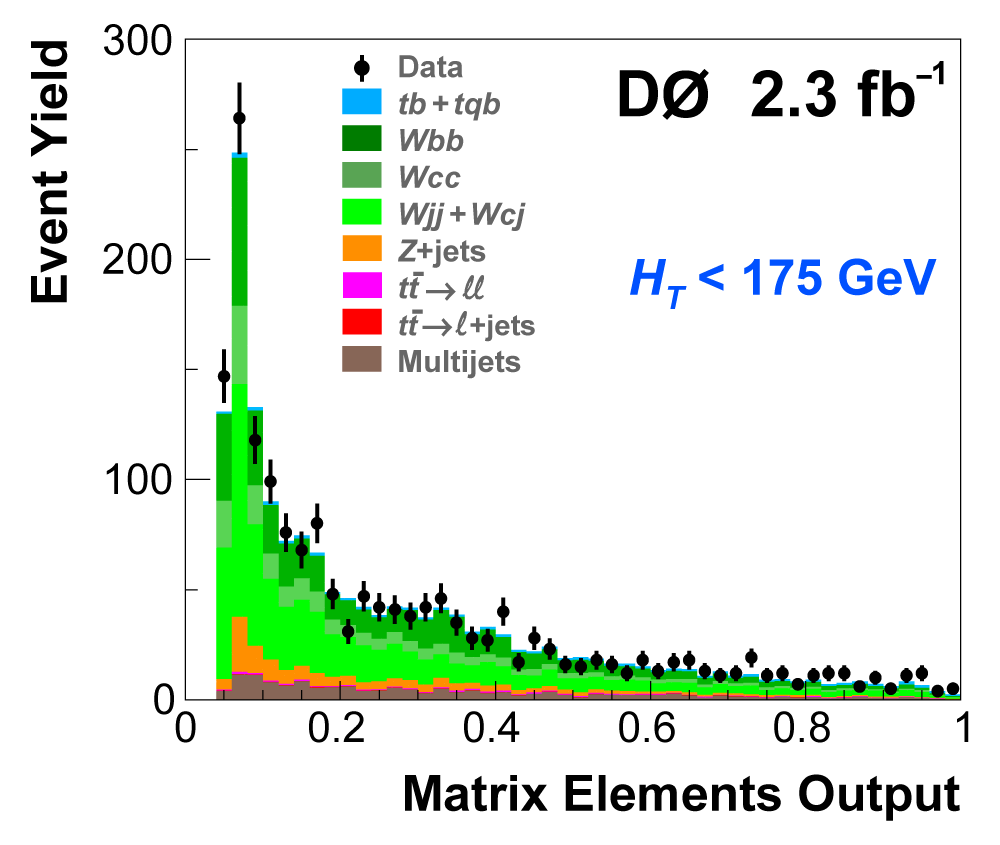
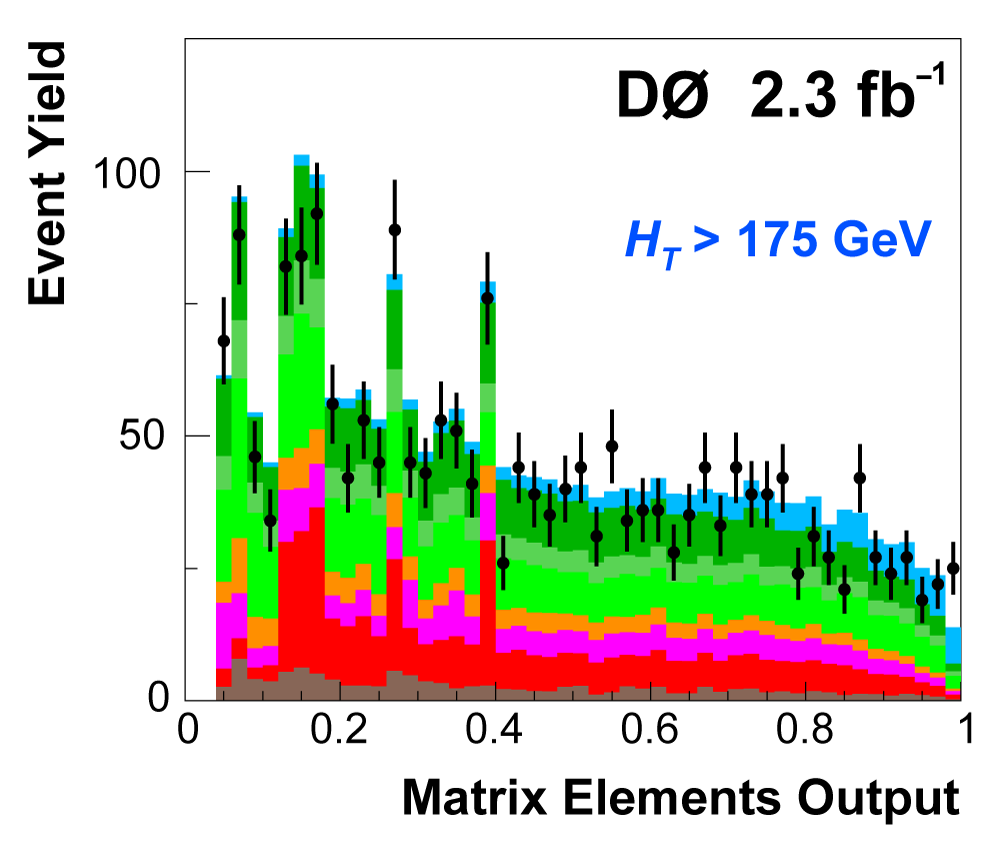
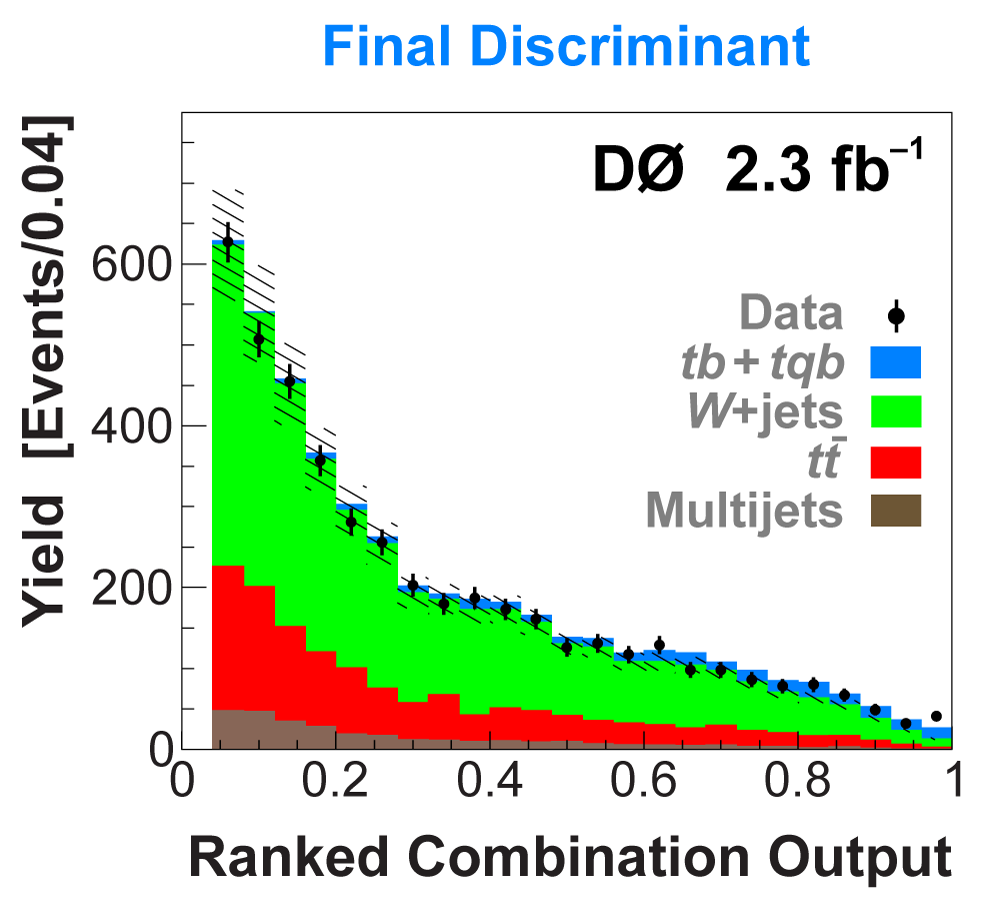
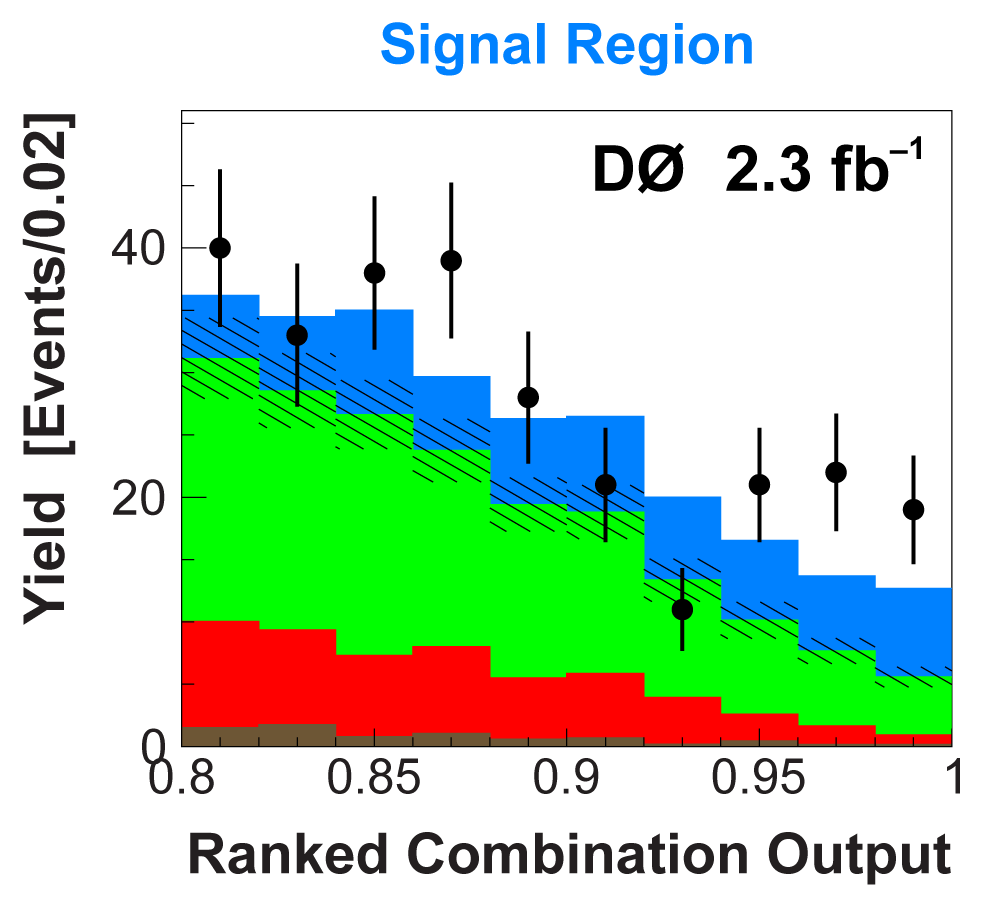
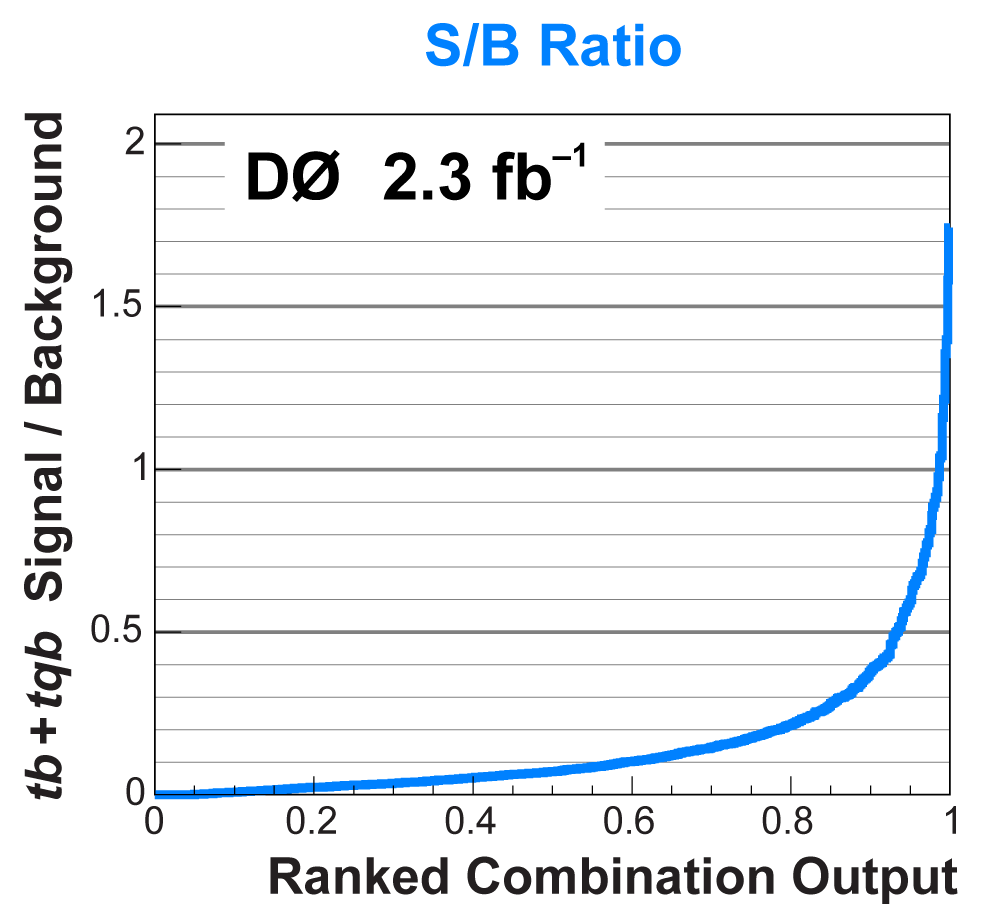
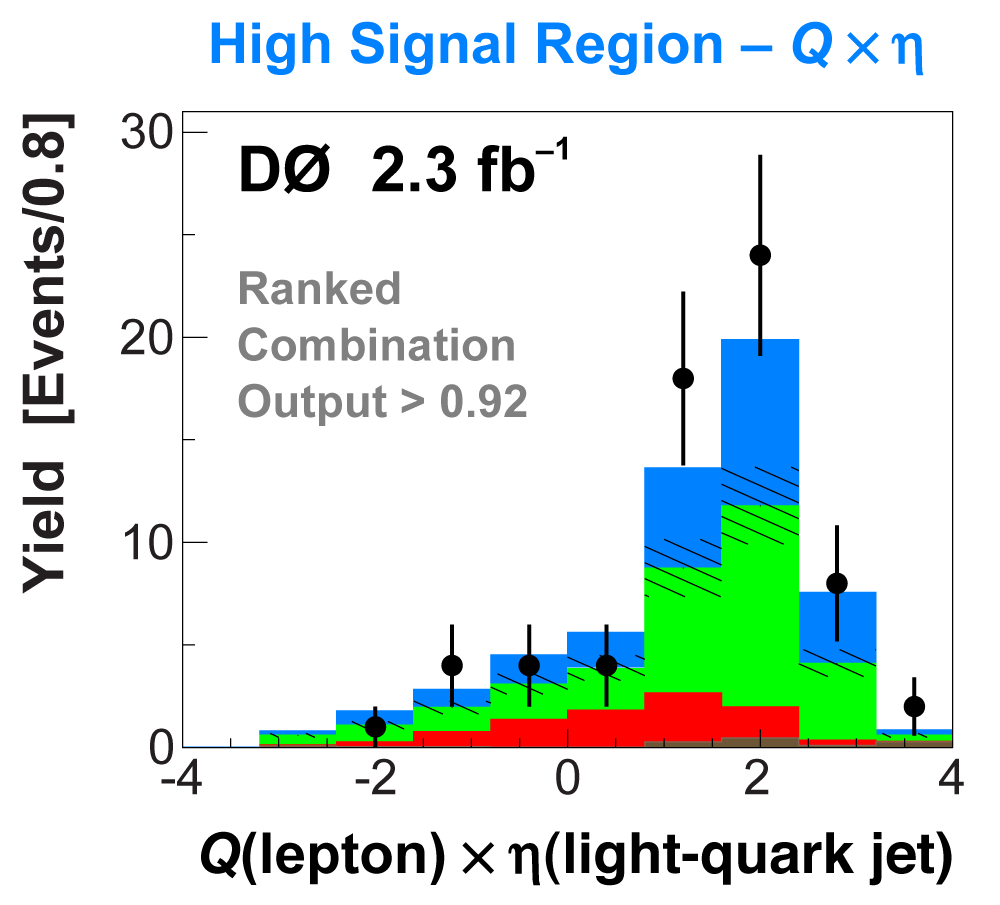
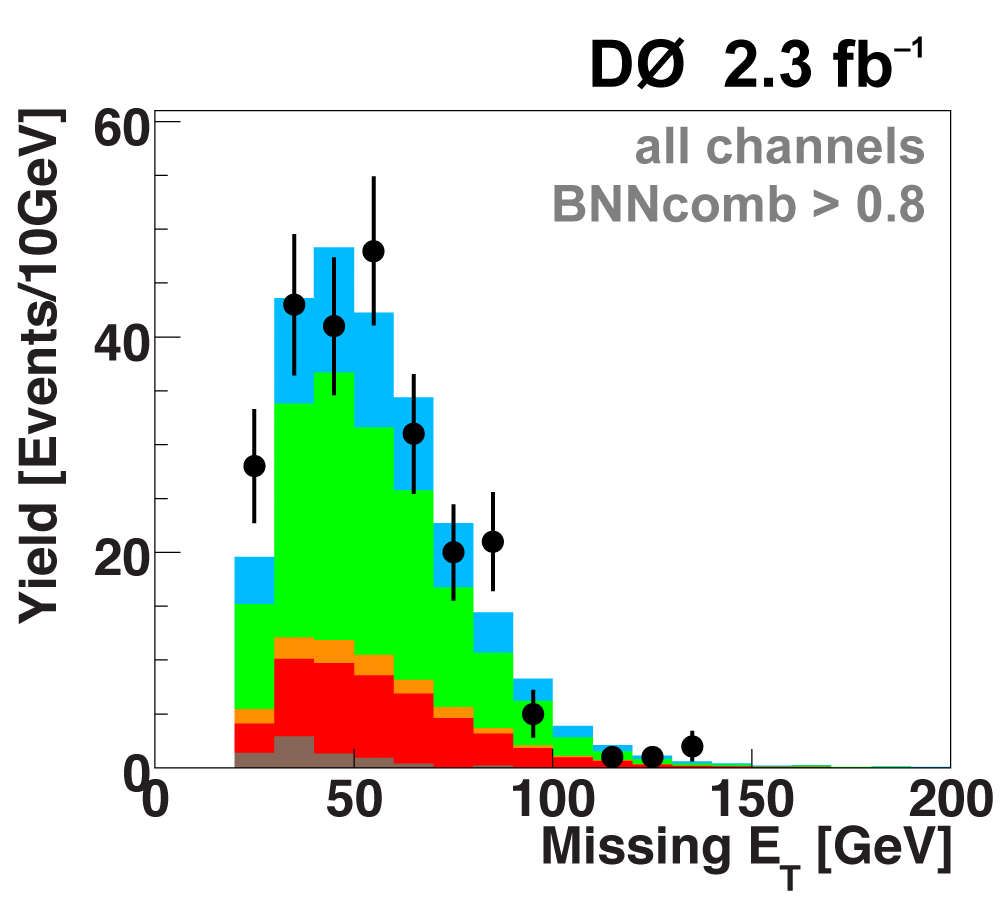
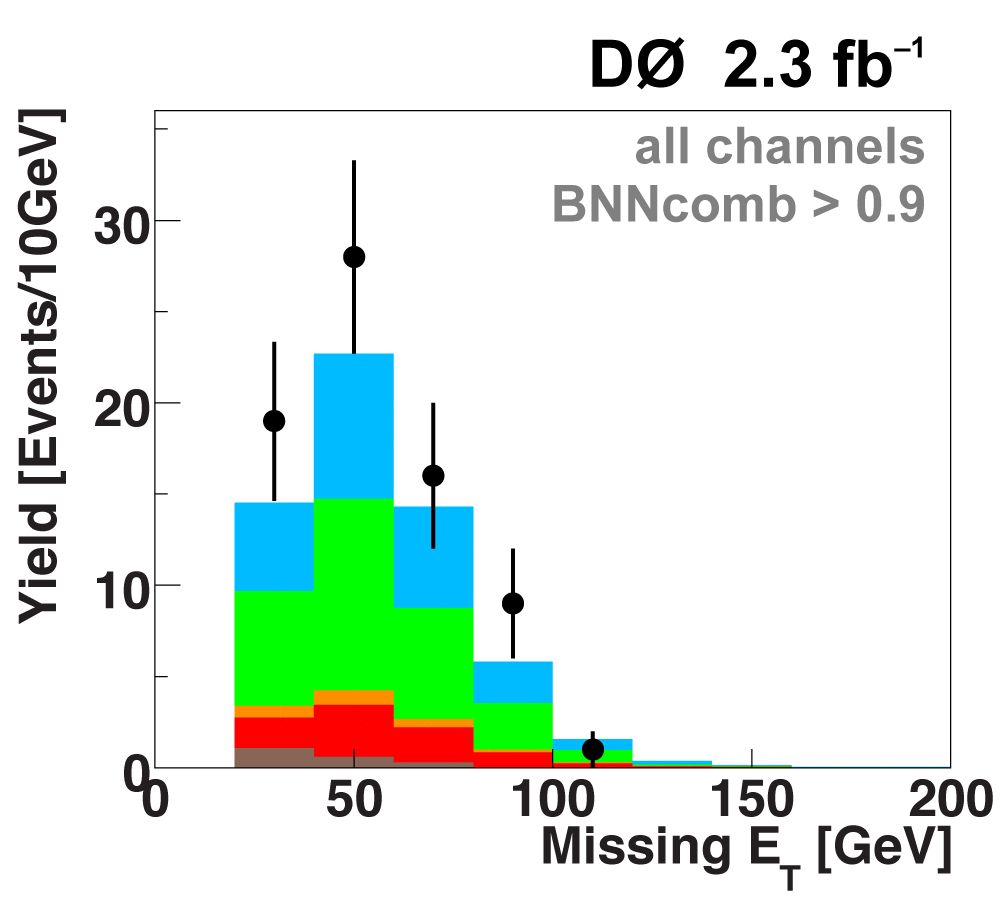
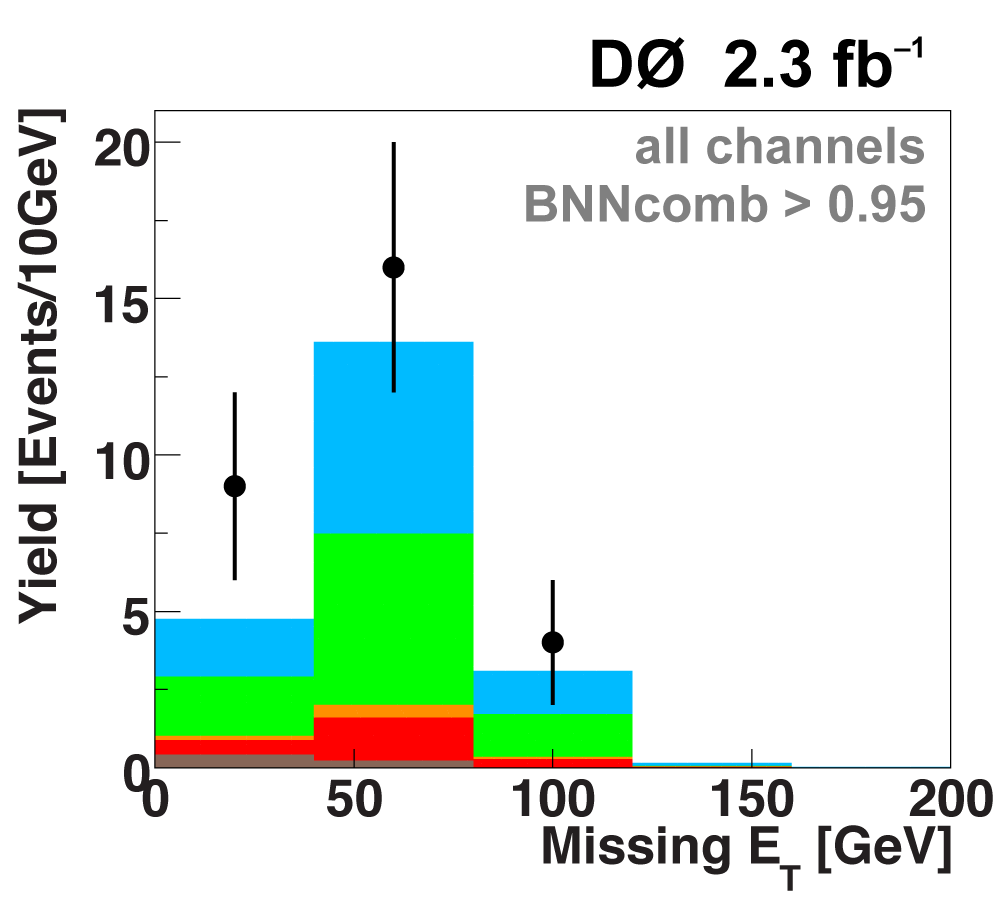
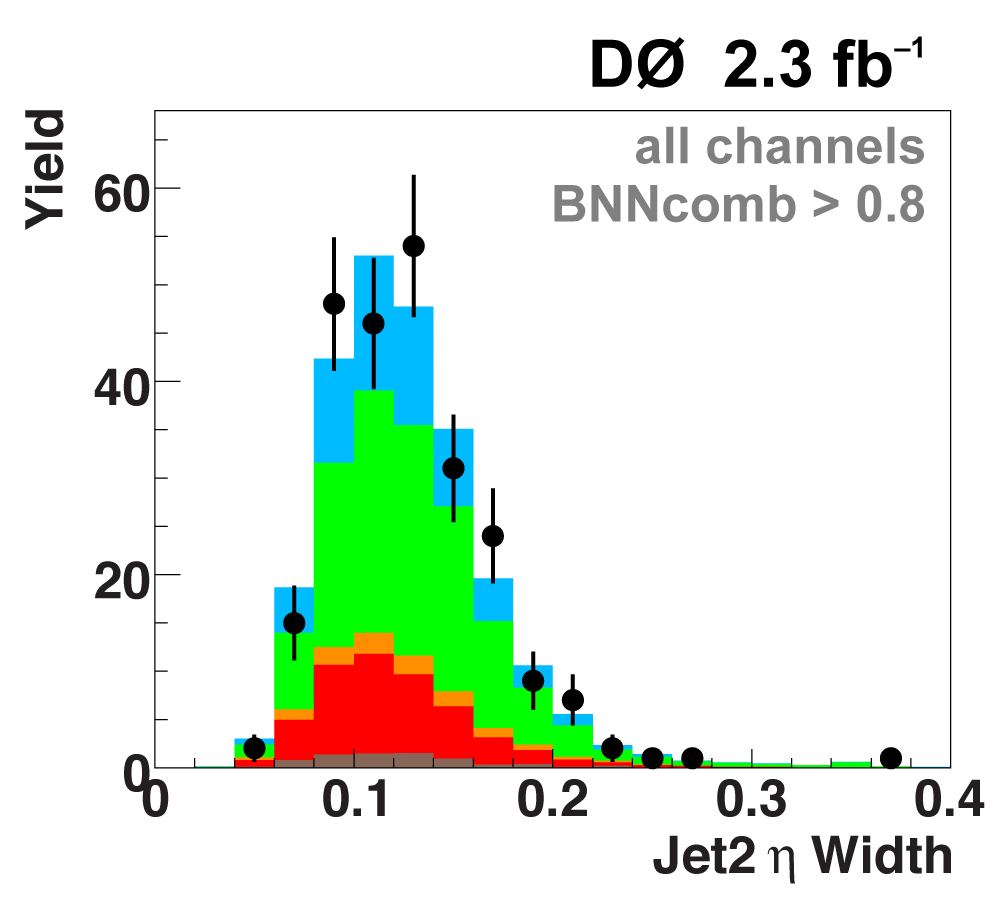
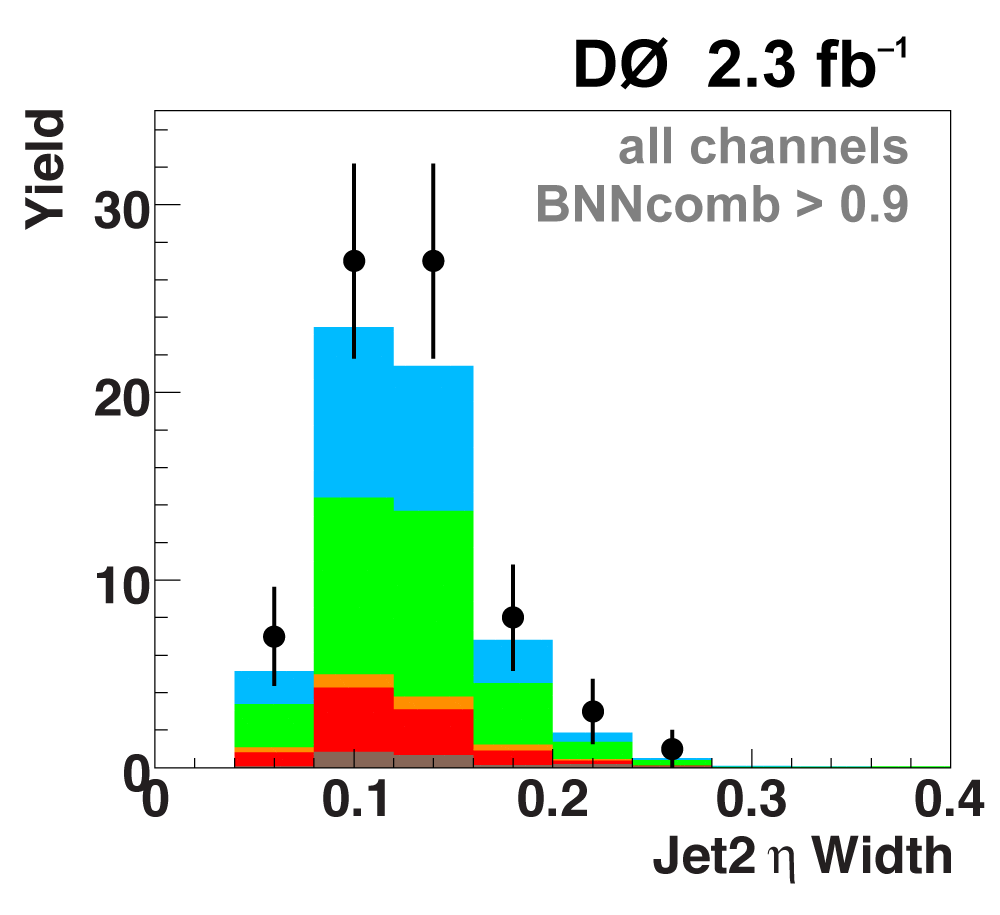
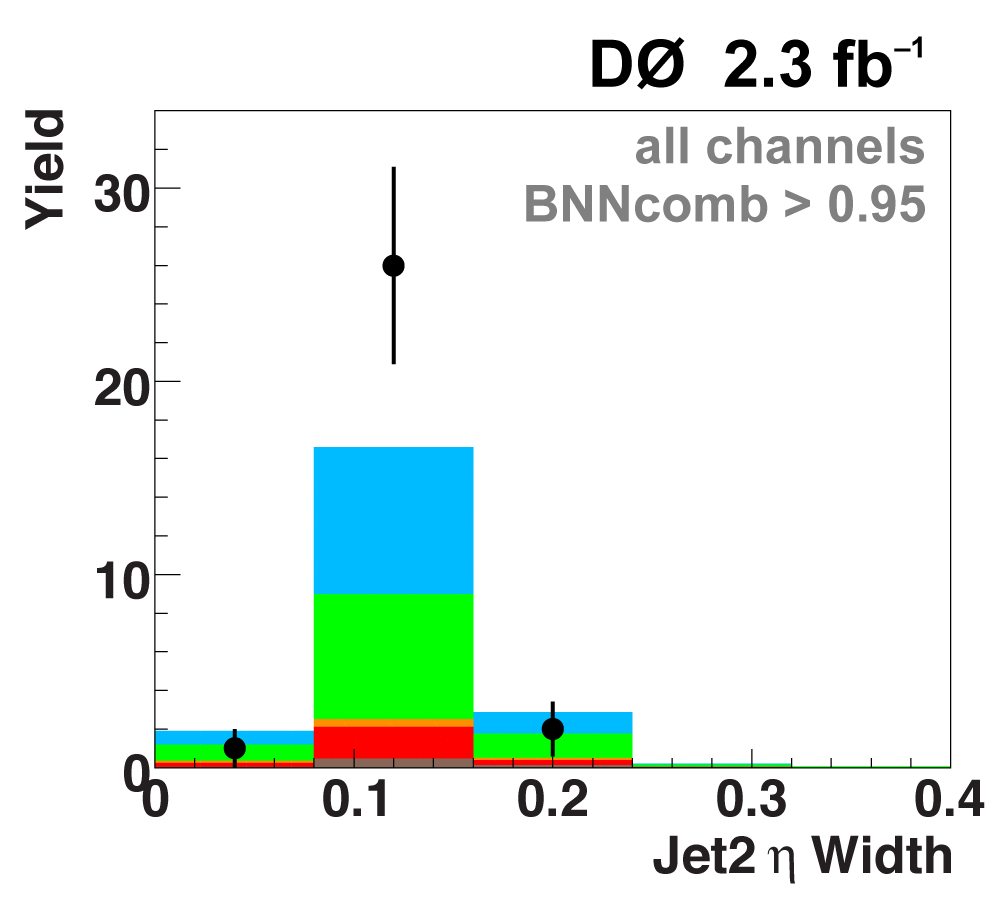
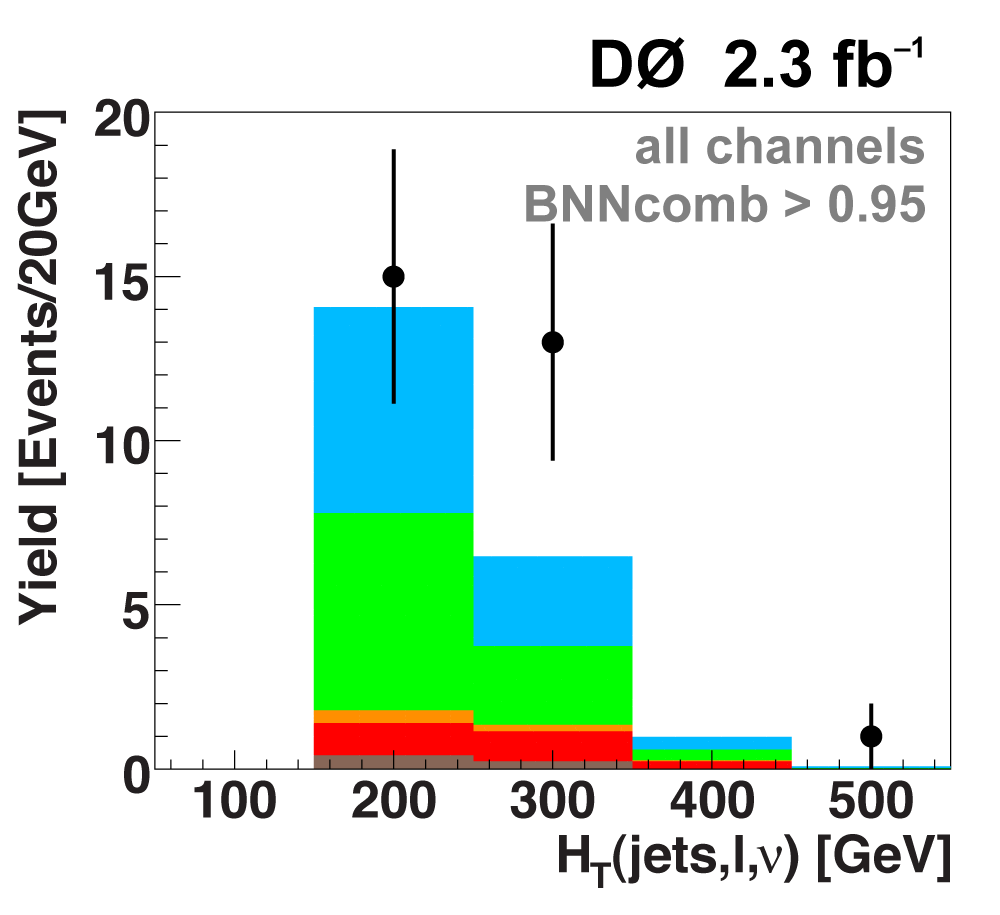
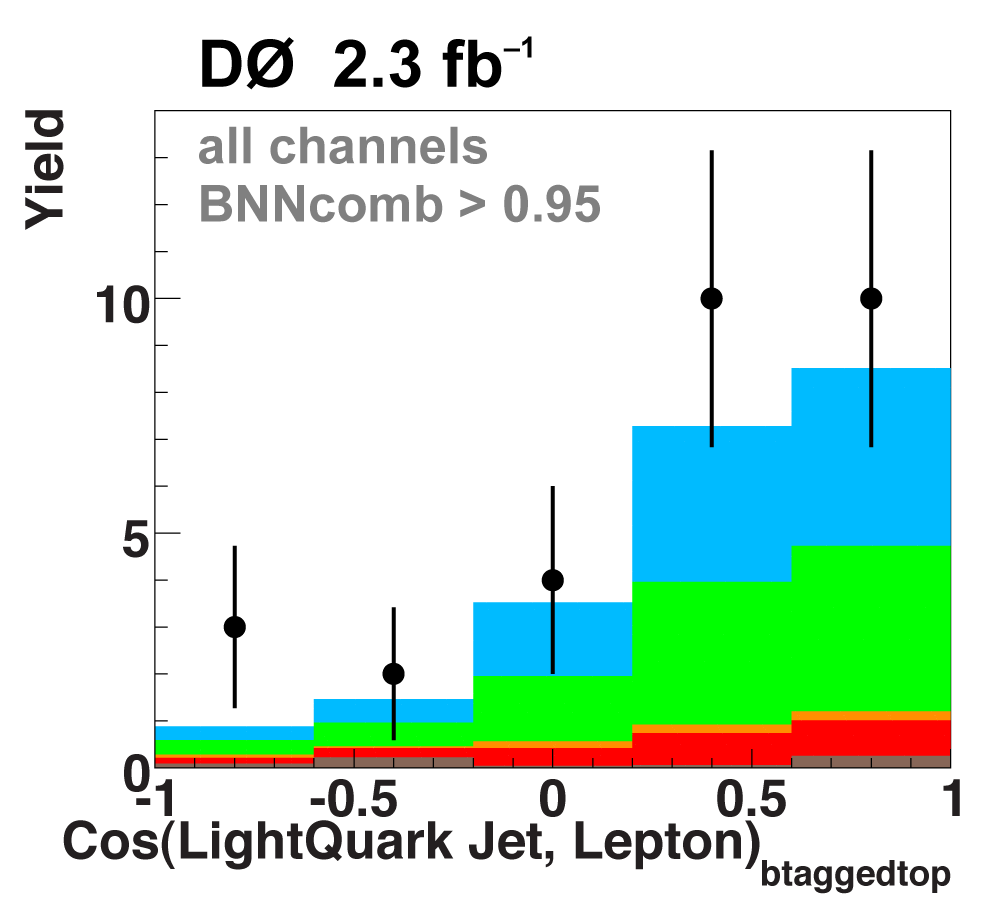
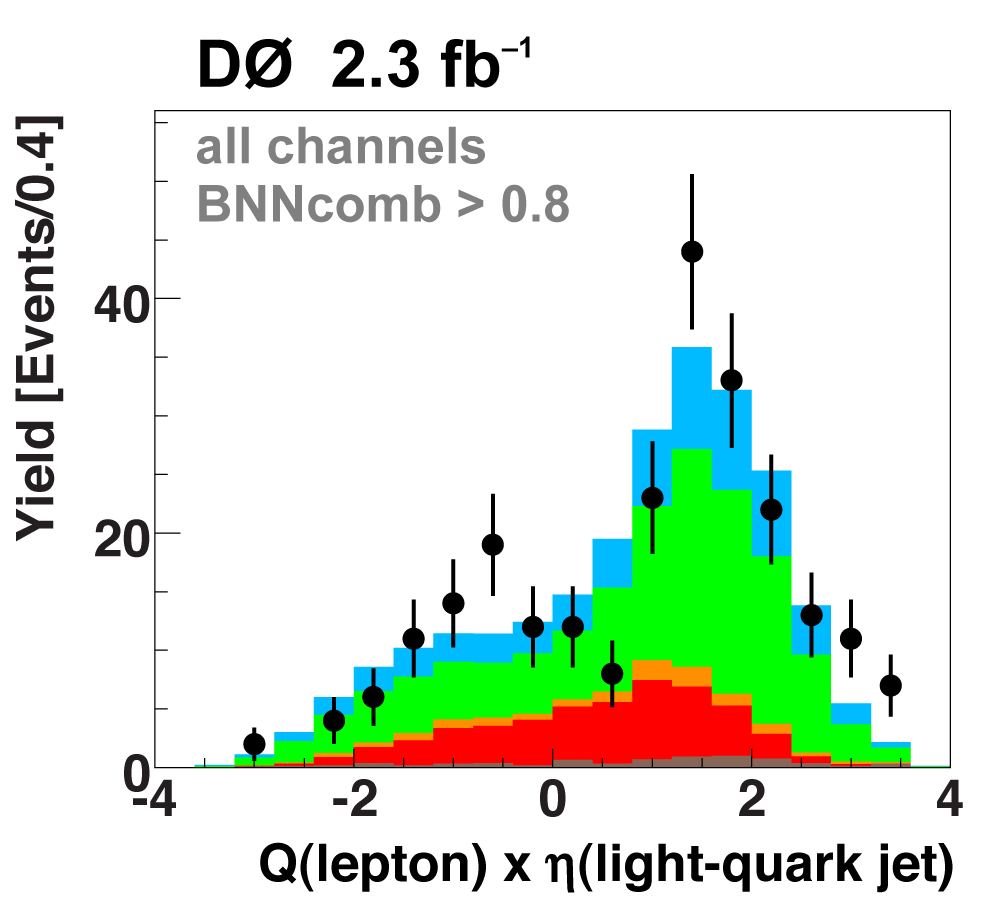
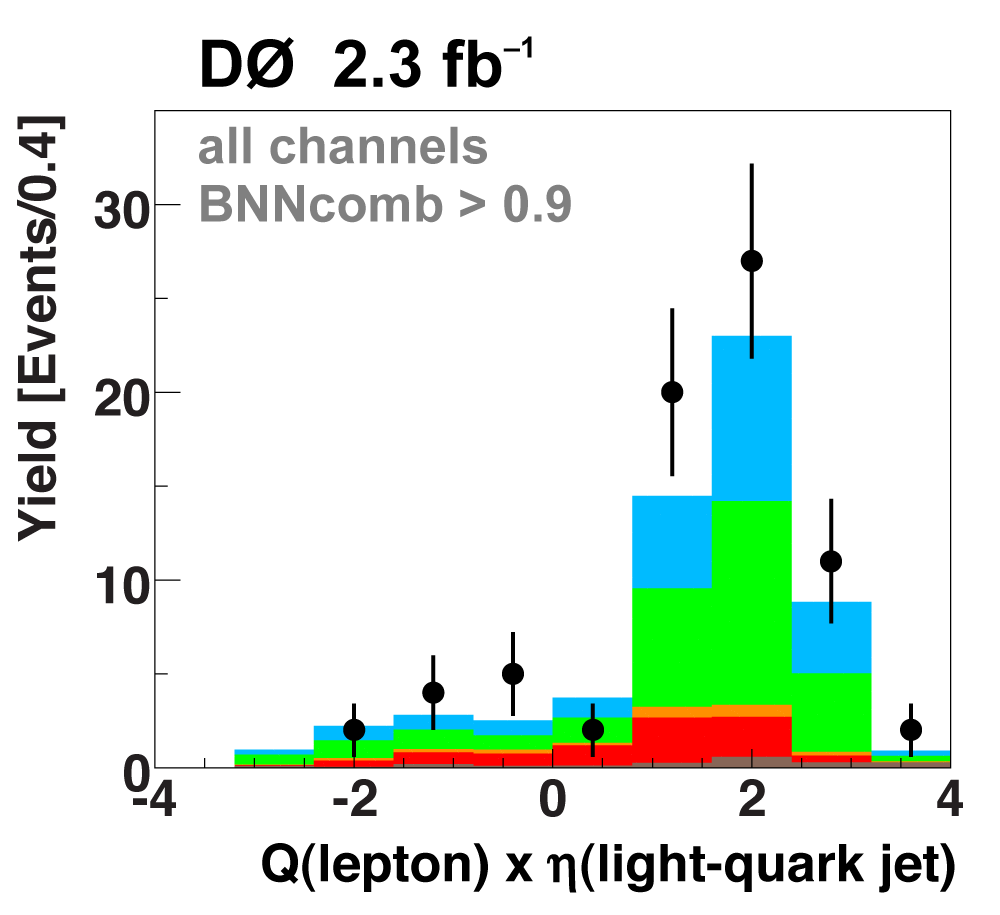
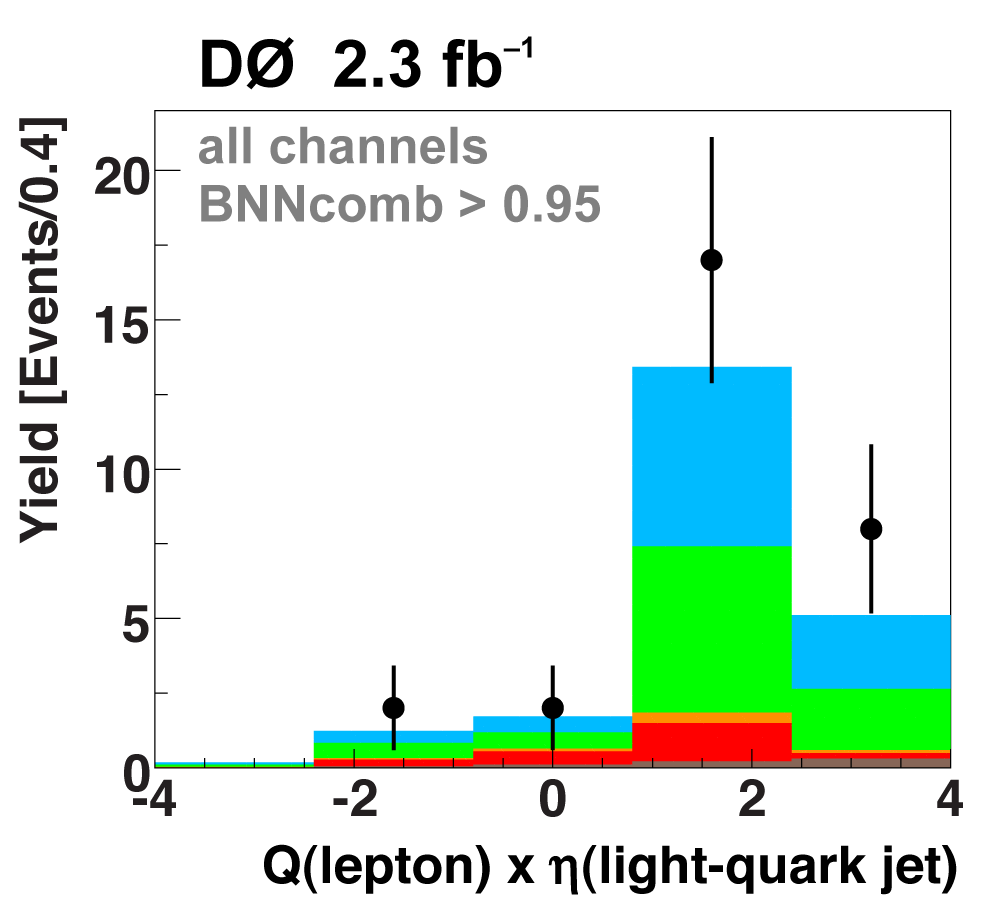
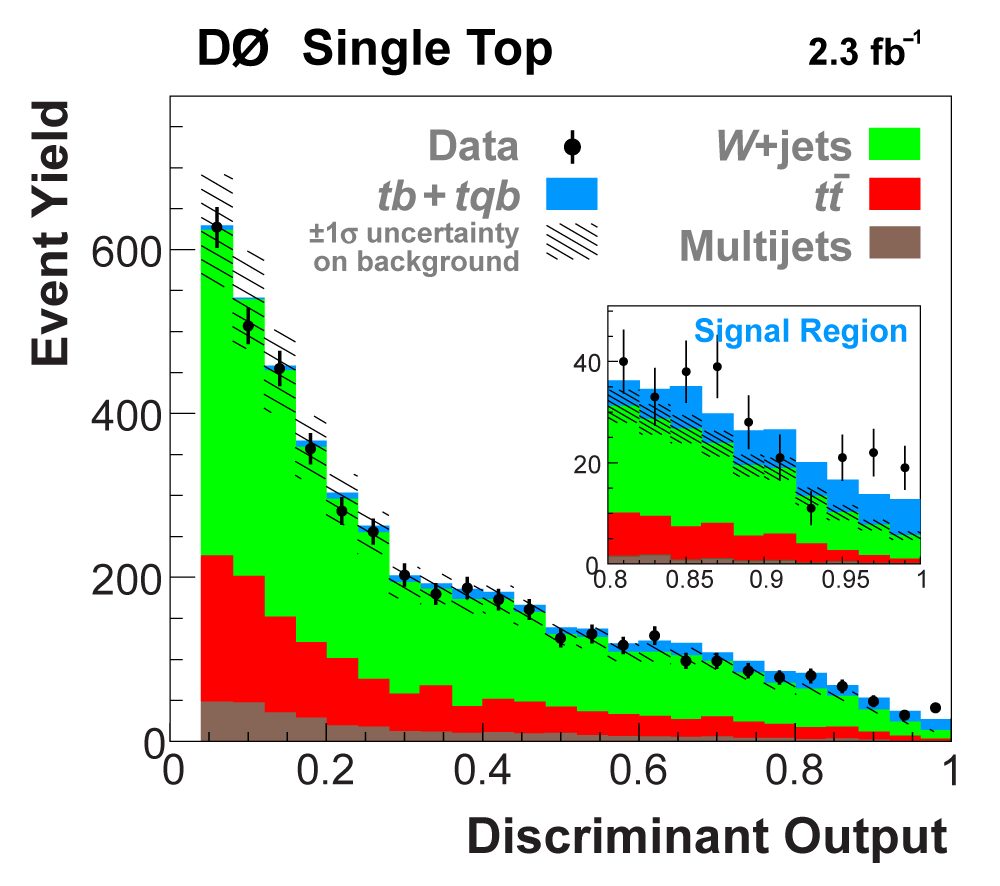
| The next four plots show the discriminant outputs for all analysis channels combined. The signal histogram uses the measured cross section value from each analysis. The spikes in the matrix element output distribution in the high-HT region come from the inclusion of sixteen separate analysis channels, some of which have lower statistics than others, and so the sub-distributions span different regions of the x-axis. |
 |
 |
 |
 |
 |
 |
 |
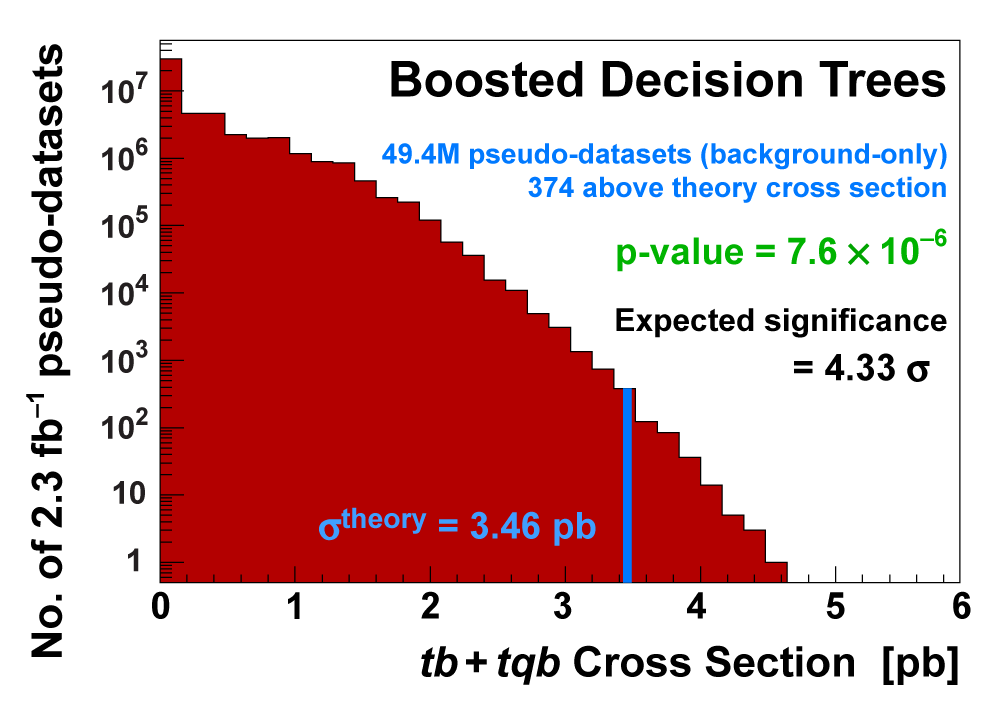
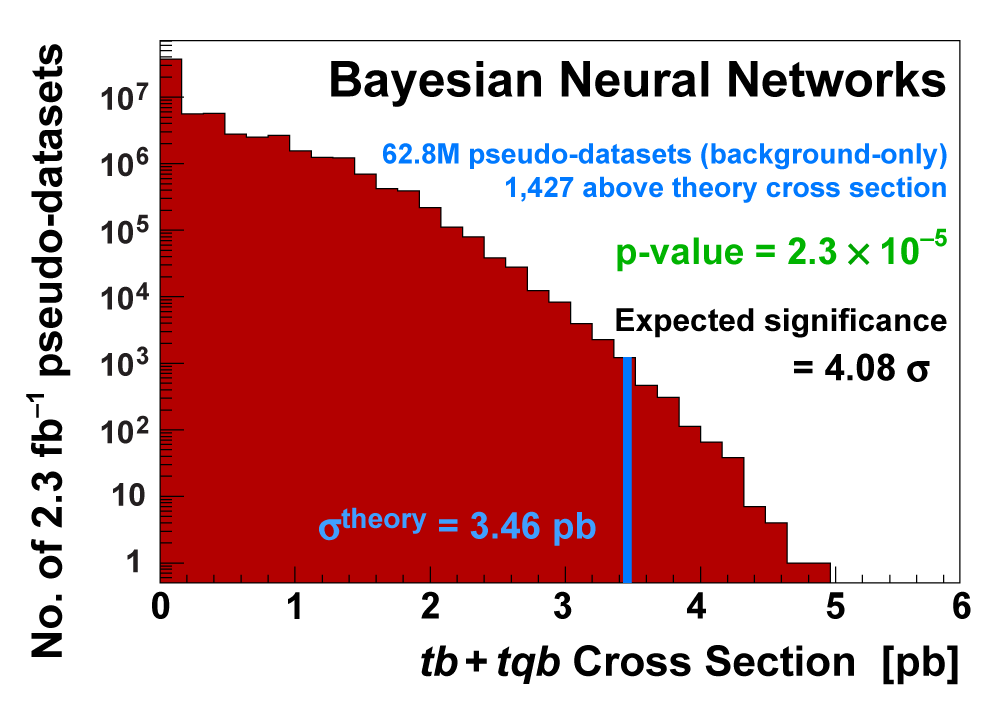
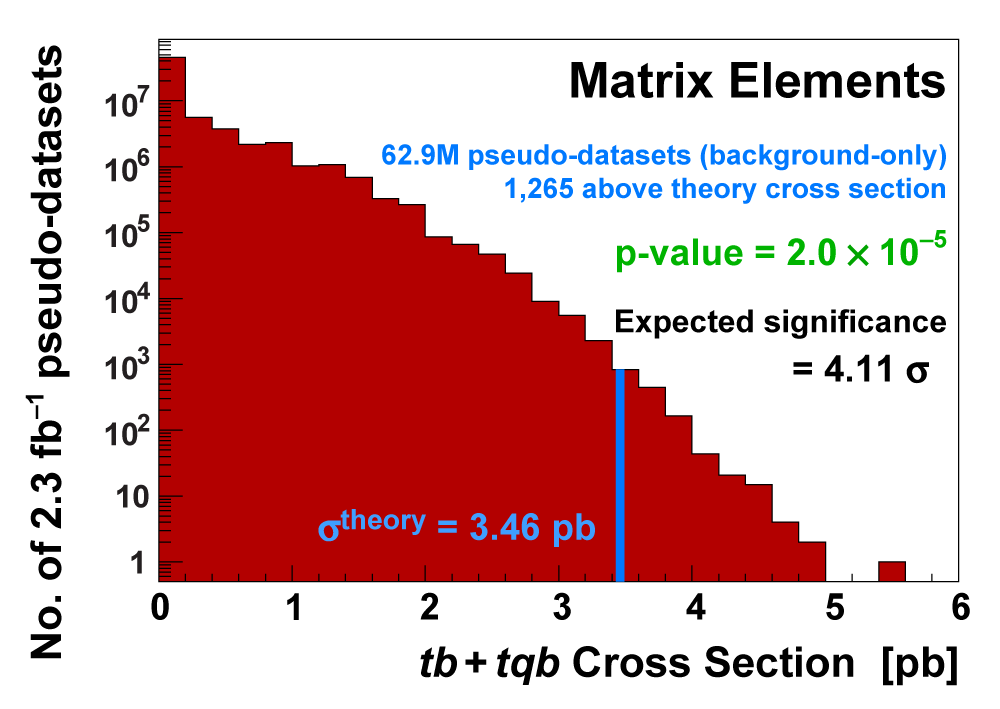
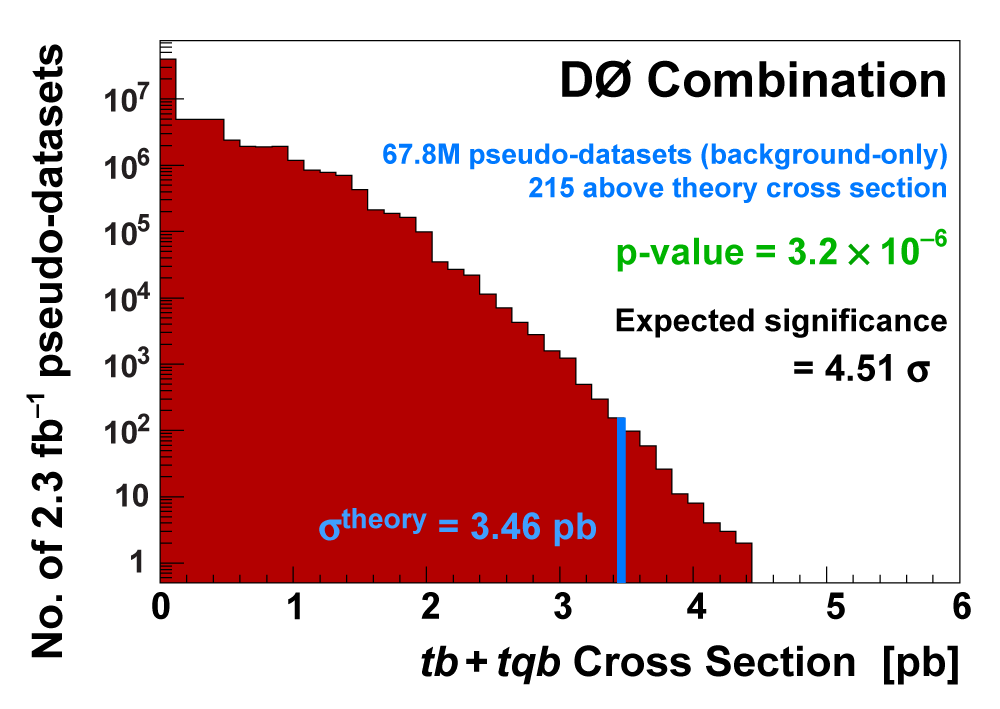
| We measure the probability for the background to fluctuate up and give a cross section measurement at least as large as the value we measure using a large ensemble of pseudo-datasets constructed using only background events and their uncertainties. This probability is known as the significance of the measurement. The cross section distributions measured on the pseudo-datasets are shown in the following three plots. |
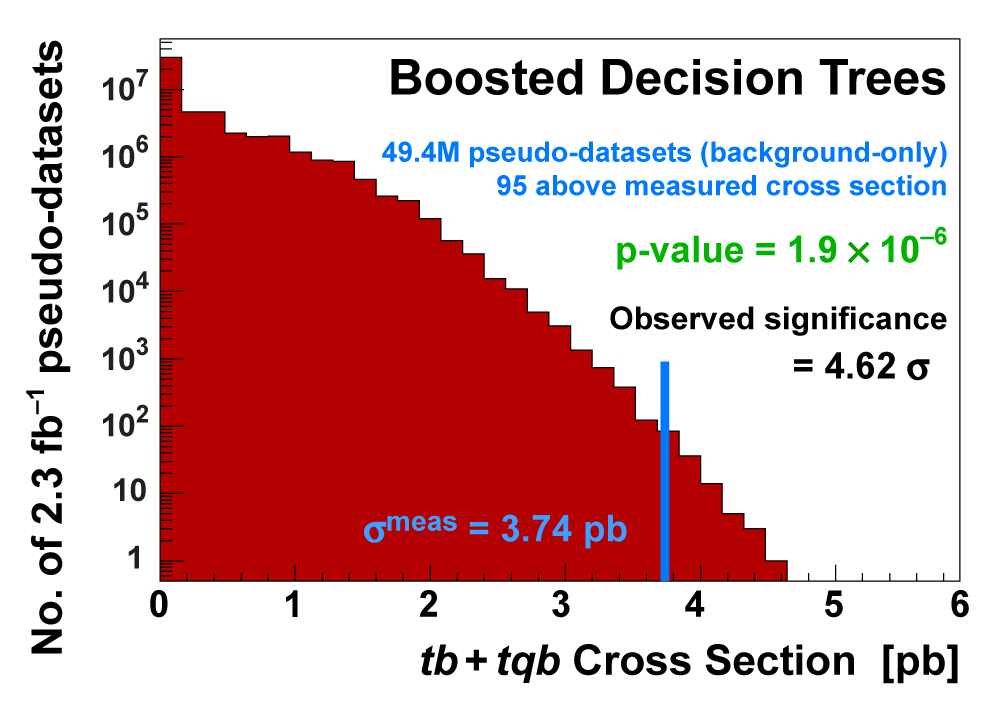 |
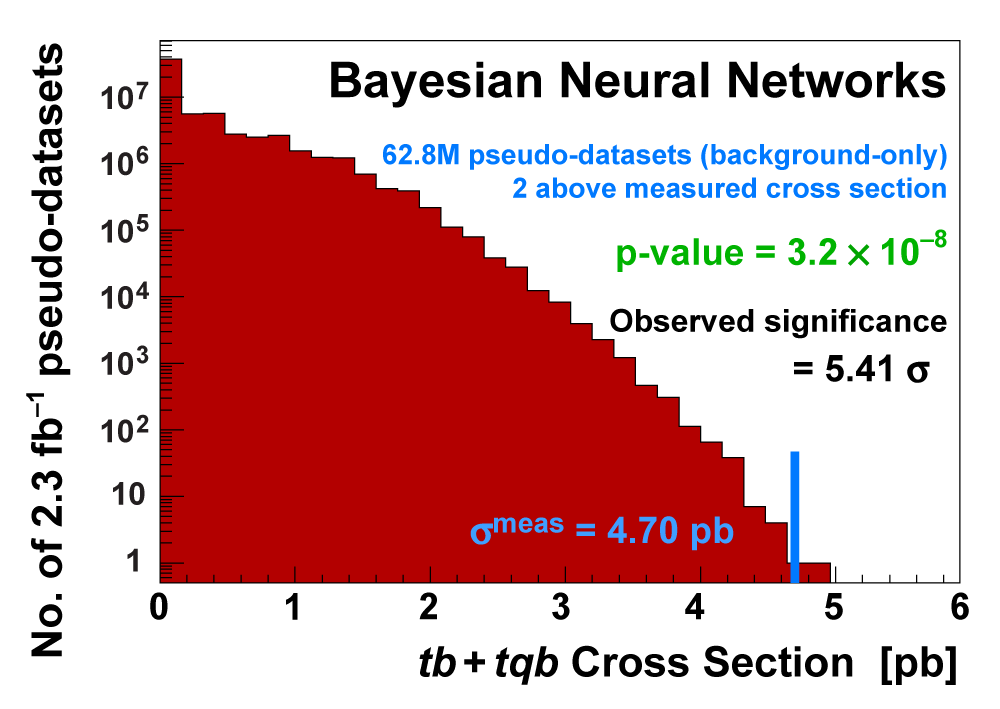 |
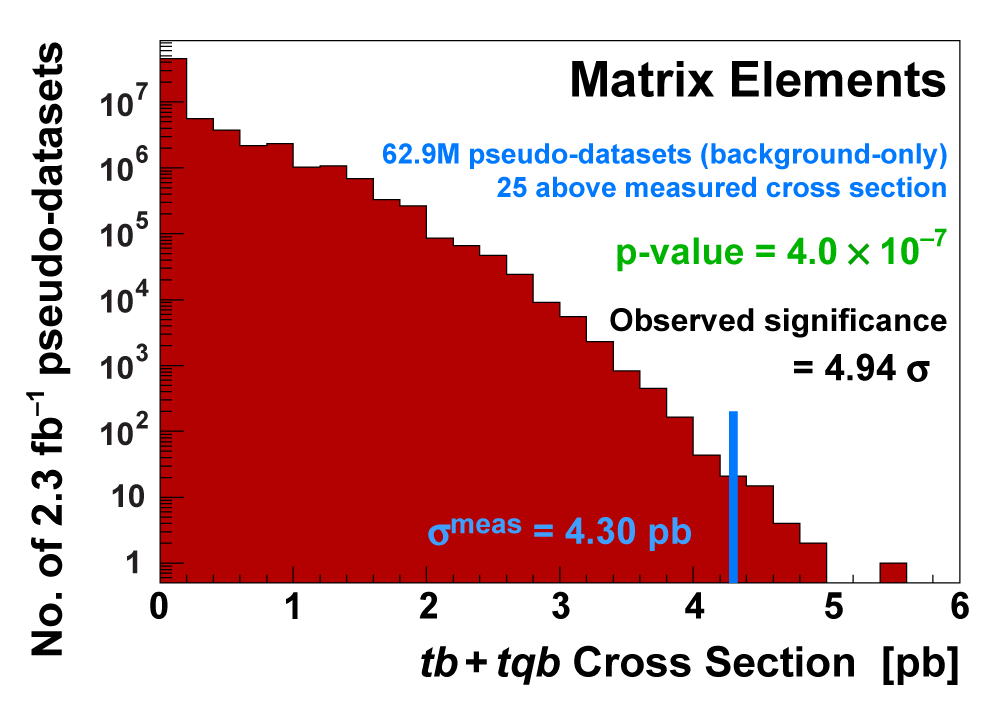 |
 |
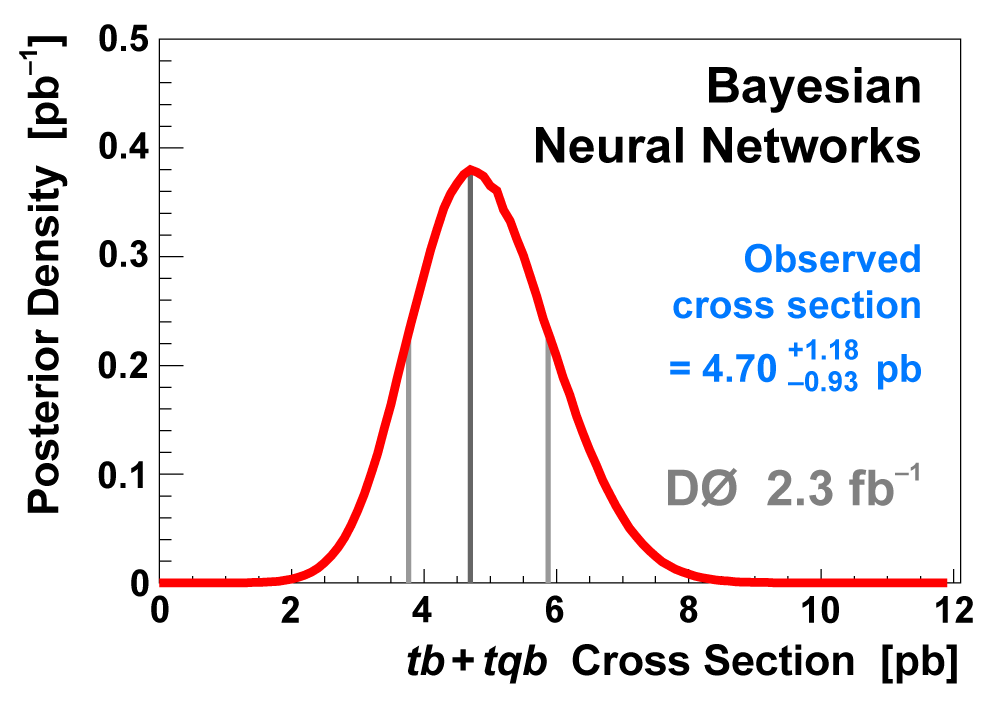
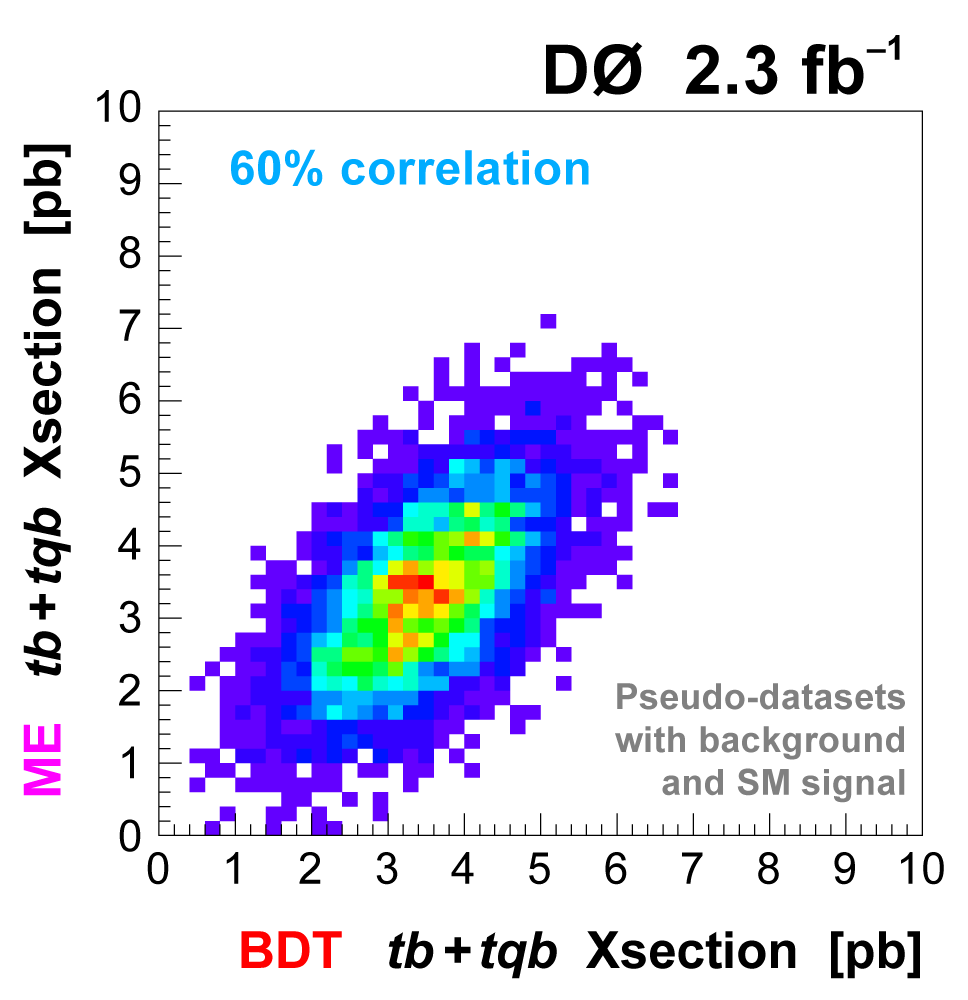
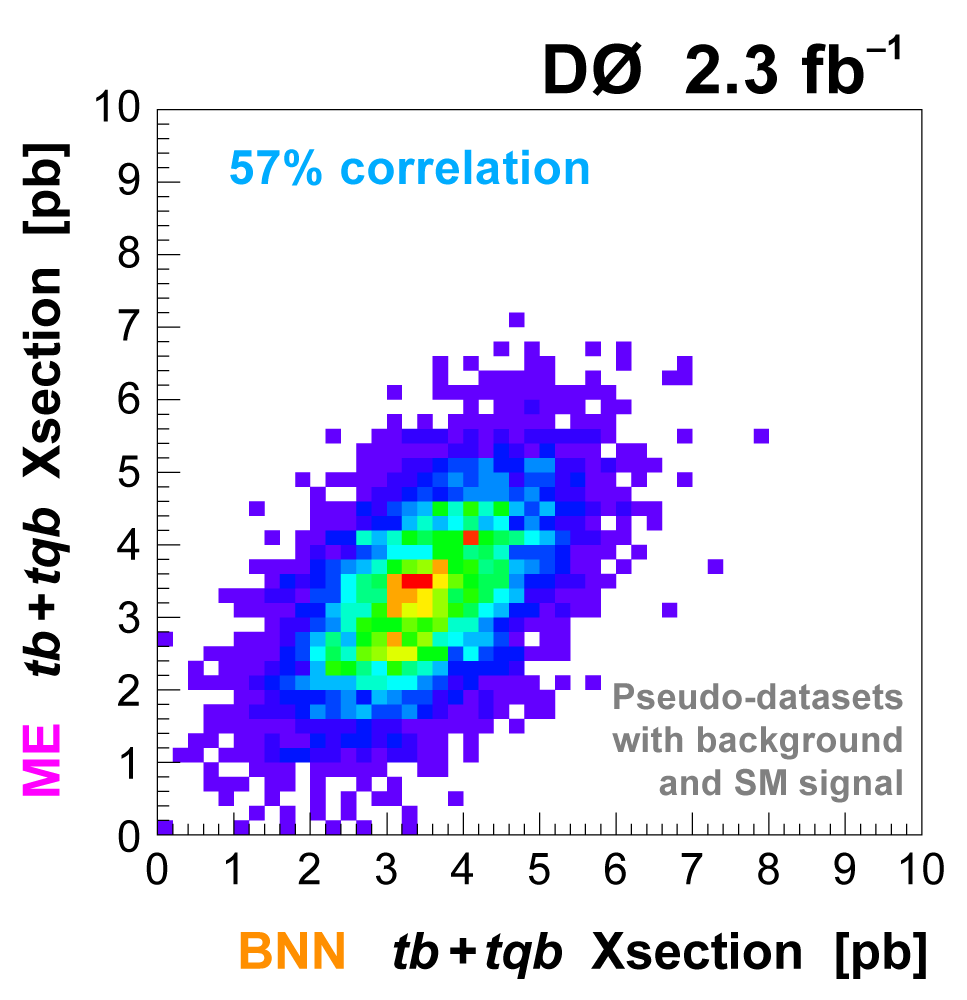
| To improve the expected significance (and hopefully the measured significance) of the measurement, we combine the output distributions from the three discriminant methods, since they are not 100% correlated. We do this by using the discriminant output distributions in each analysis channel as inputs to a Bayesian neural network trained to do the combination. The BNNs have six hidden nodes. The following plots show the results of this combination. |
 |  |
 |
|
 |
 |
 |
 |
|
| The signal histogram (shown in blue) uses the measured cross section value for normalization, for the discriminant output plots shown here and for the following two plots of sensitive variables. Please see lower down on this page for a version of the final discriminant plot with the zoomed-in high-signal region inset, suitable for review talks and proceedings papers. |
 |
 |
 |
 |
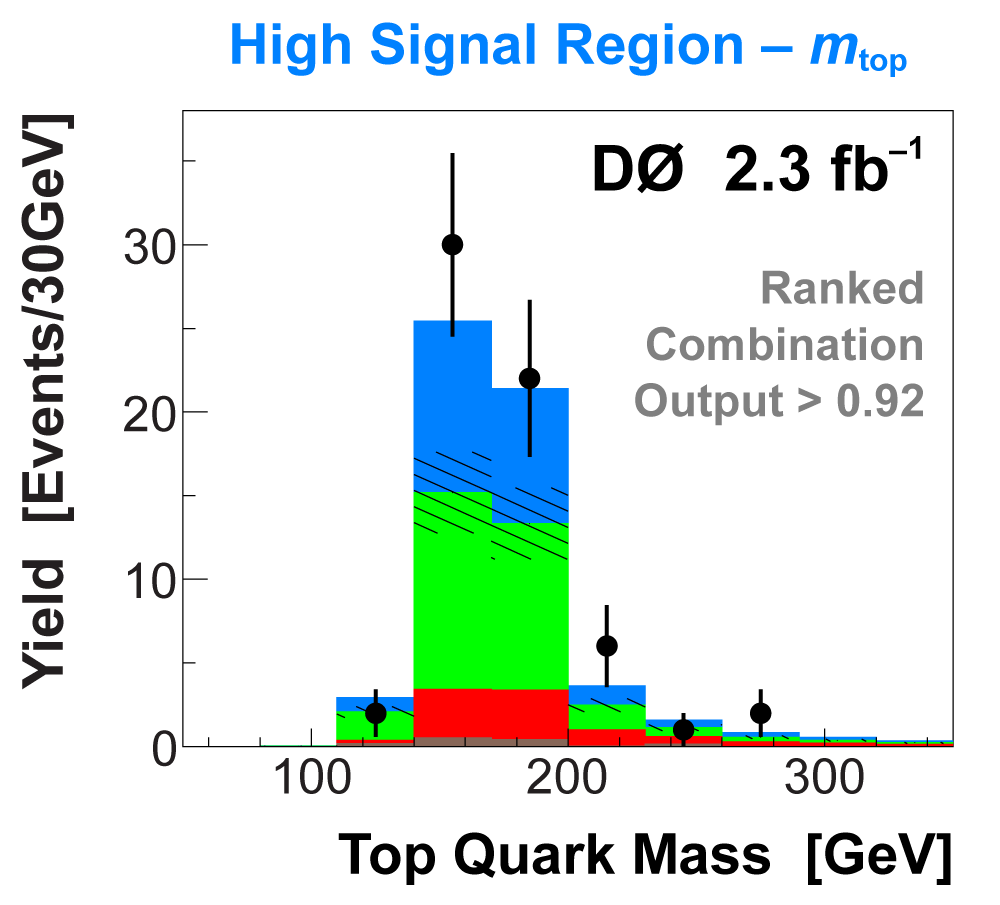 |
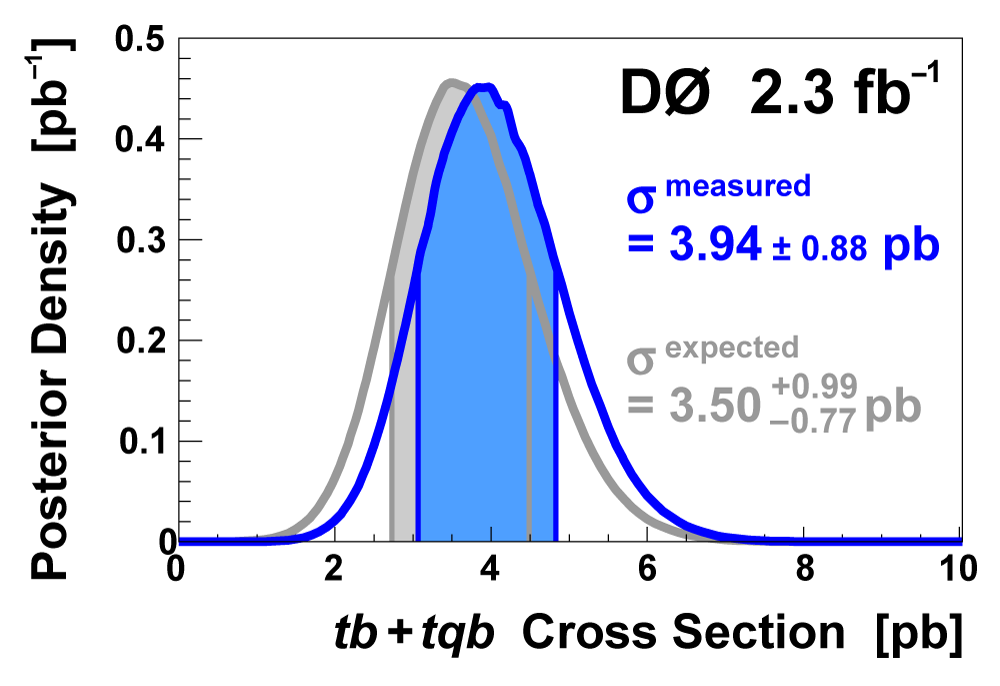 |
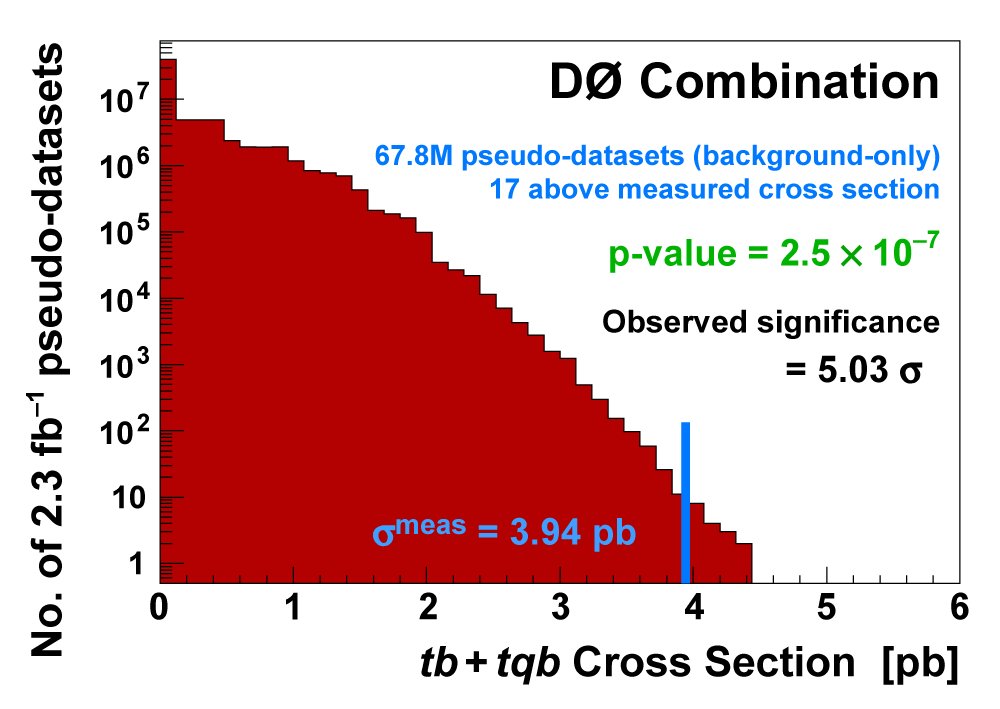 |
| The following two plots show cumulative events versus cumulative signal (left plot is full scale, 223 signal events on the x-axis, right plot is a zoom-in of the high-signal region); the format has been developed for the Higgs boson search at the Tevatron. The plots provide an interesting new way of illustrating the presence of signal in a dataset. (Of course, in the Higgs search thus far, all data points lie along the background-only (green) line, since no signal has been seen.) The plots are created starting from the discriminant output plot with bins ranked in order of signal/background (as shown above), and for each predicted signal event, starting from the highest signal/background bin and working down, the cumulative background events (green solid line), background+signal events (blue dashed line), and data events are summed. Thus every point on the lines and the data points contain the points to the left of them and they are highly correlated. If there were no signal in the data, then the data points would lie around the background prediction line. When there is signal present, the data points cluster around the background+signal prediction, as seen in these plots. If there were not much signal predicted in the data, then the two lines would be very close together and the data could not tell the predictions apart. The plots clearly show that the data is incompatible with the background-only prediction and consistent with background+signal. |
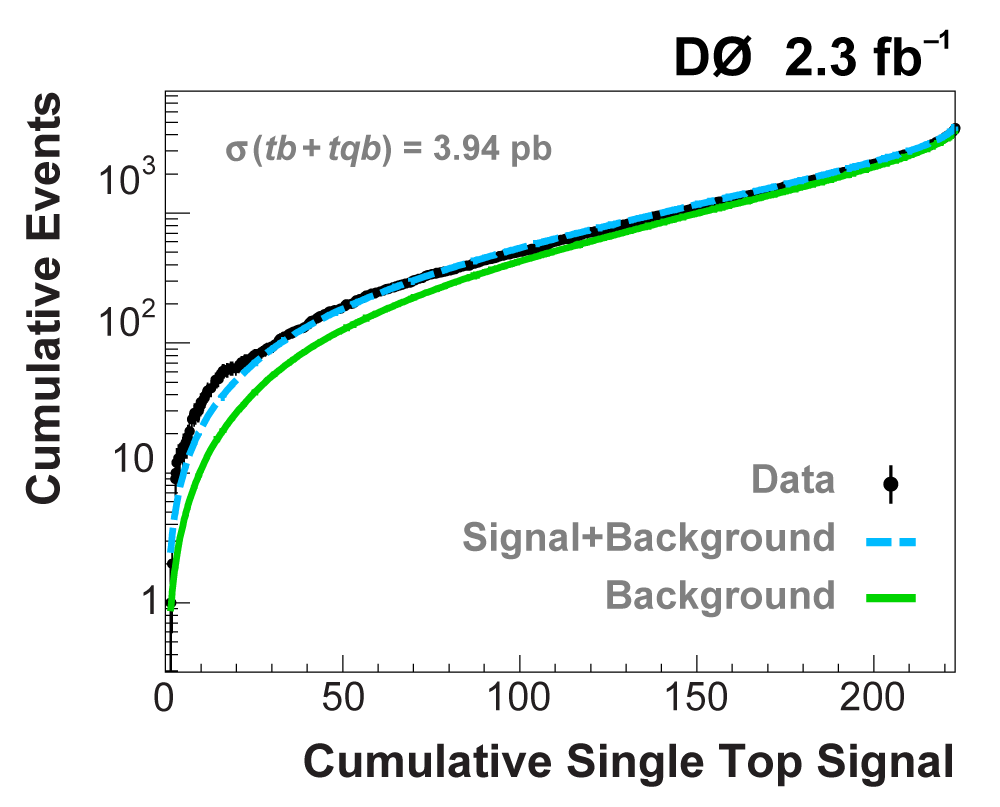 |
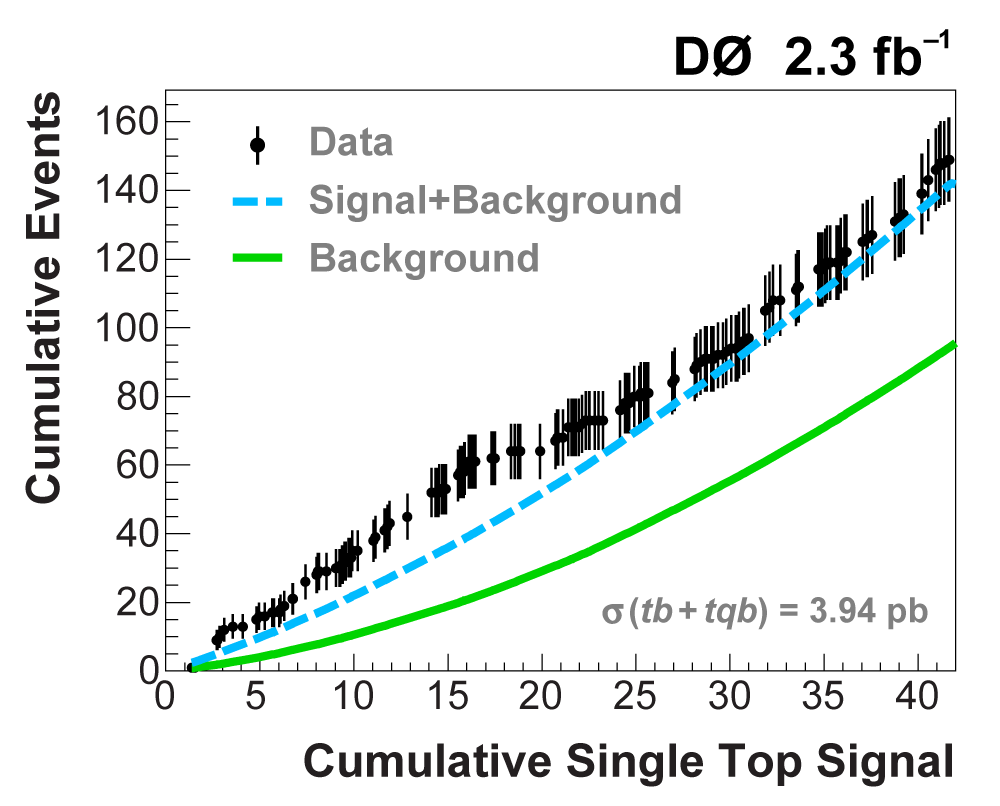 |
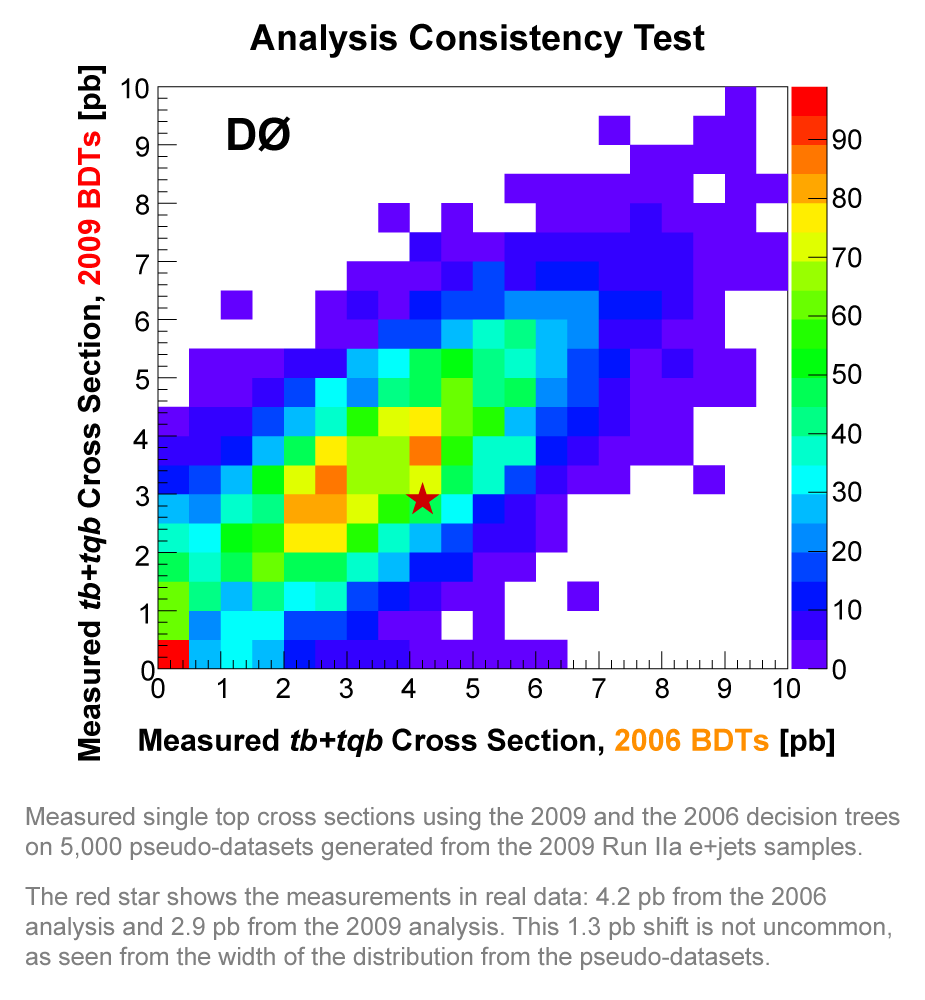
| In addition to the combination using a Bayesian neural network, we also combine the three sets of results using the Best Linear Unbiased Estimate (BLUE) method. This forms a valuable cross-check of the final result. Calculation of the significance of this result is in progress. |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
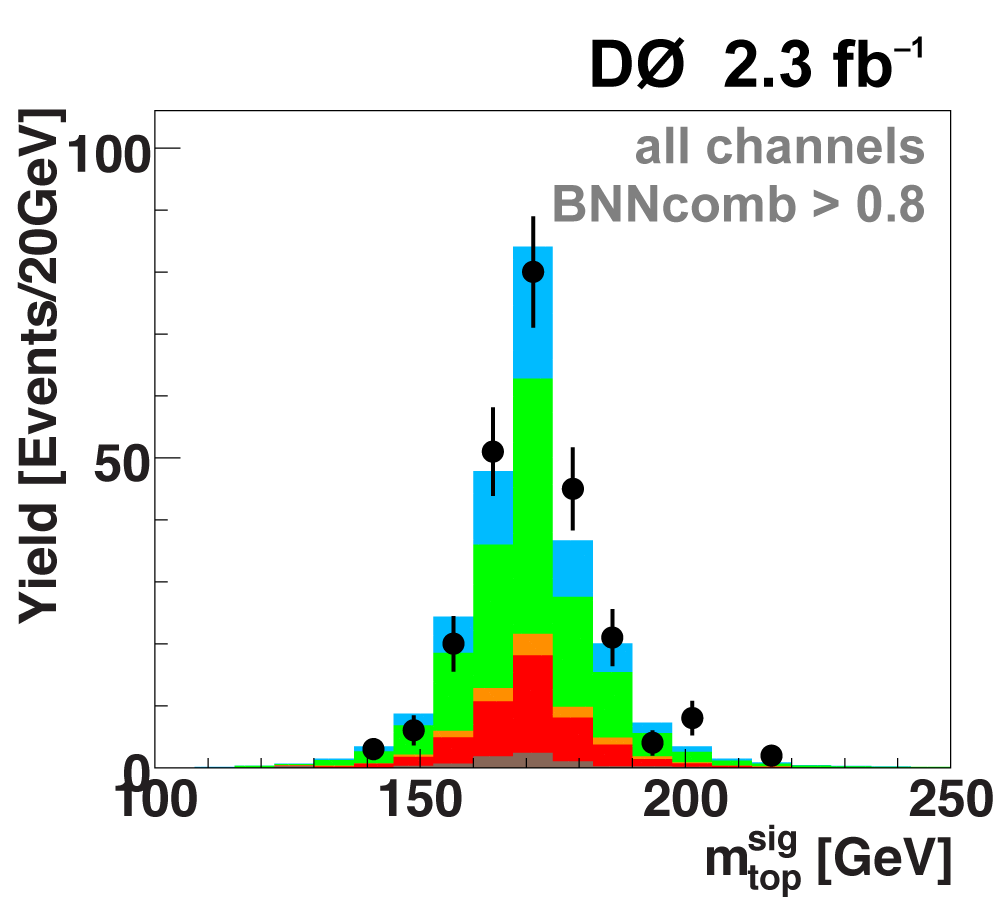 |
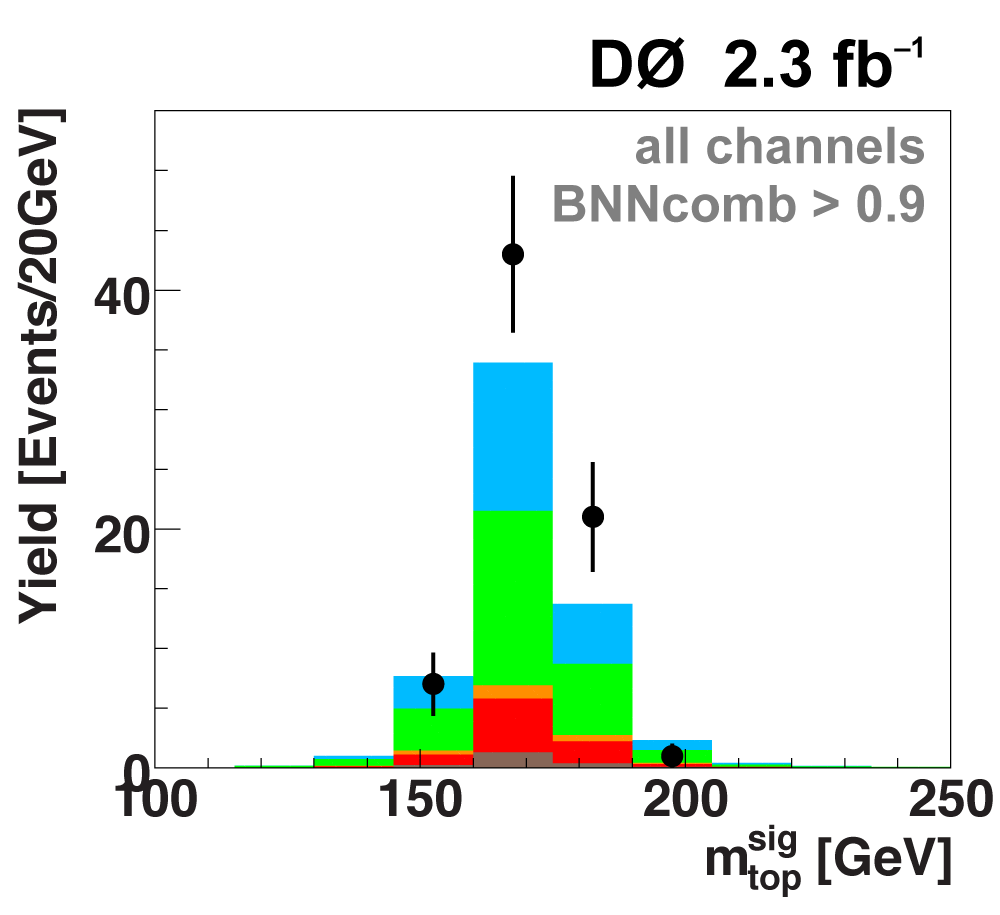 |
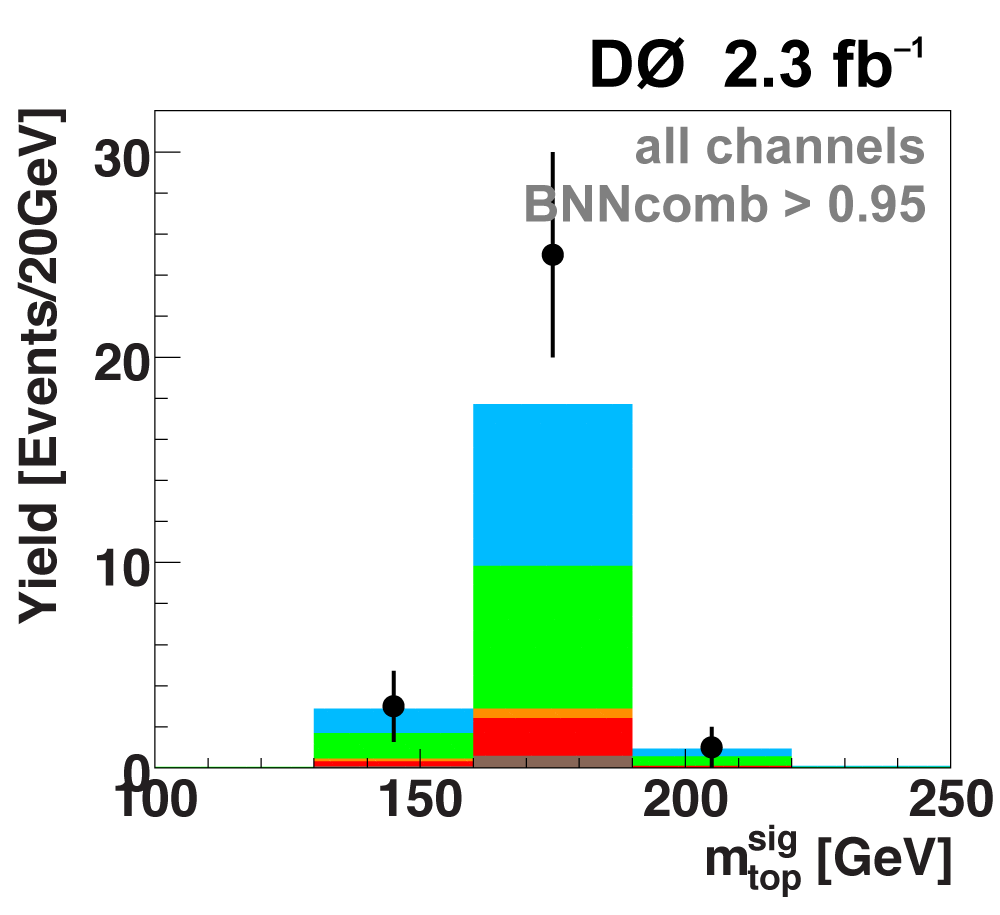 |
|
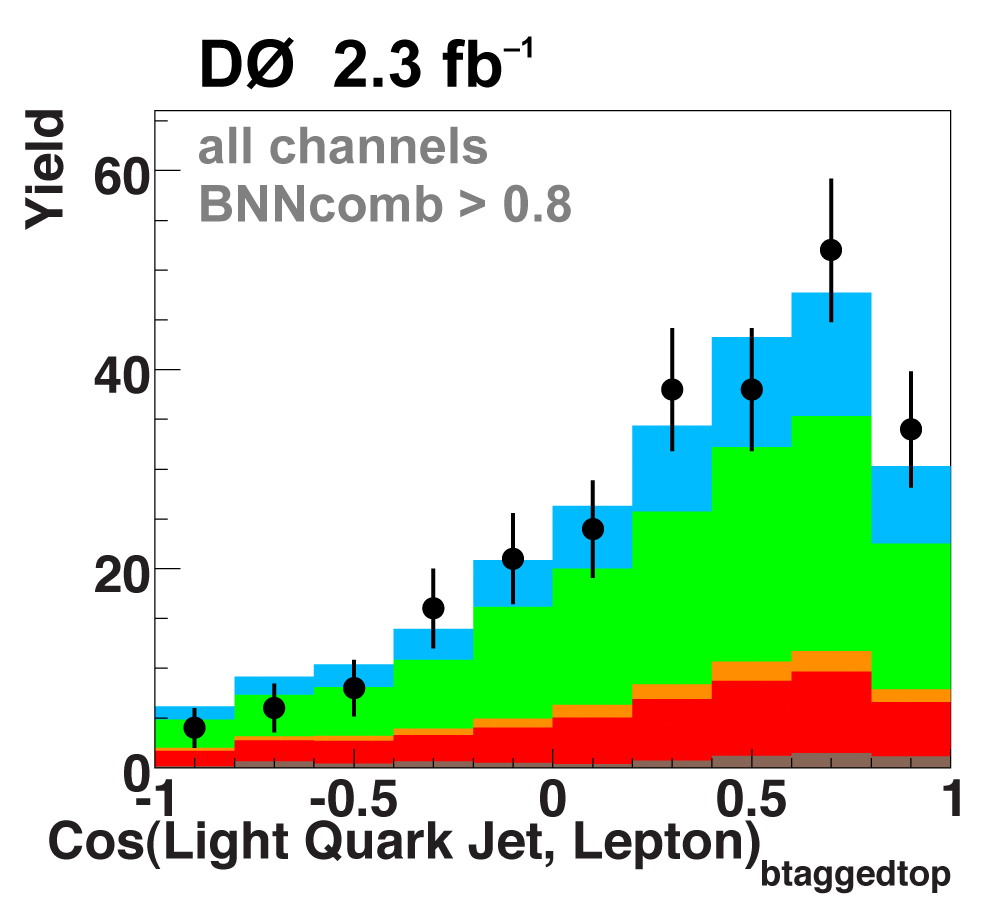 |
 |
 |
 |
 |
 |
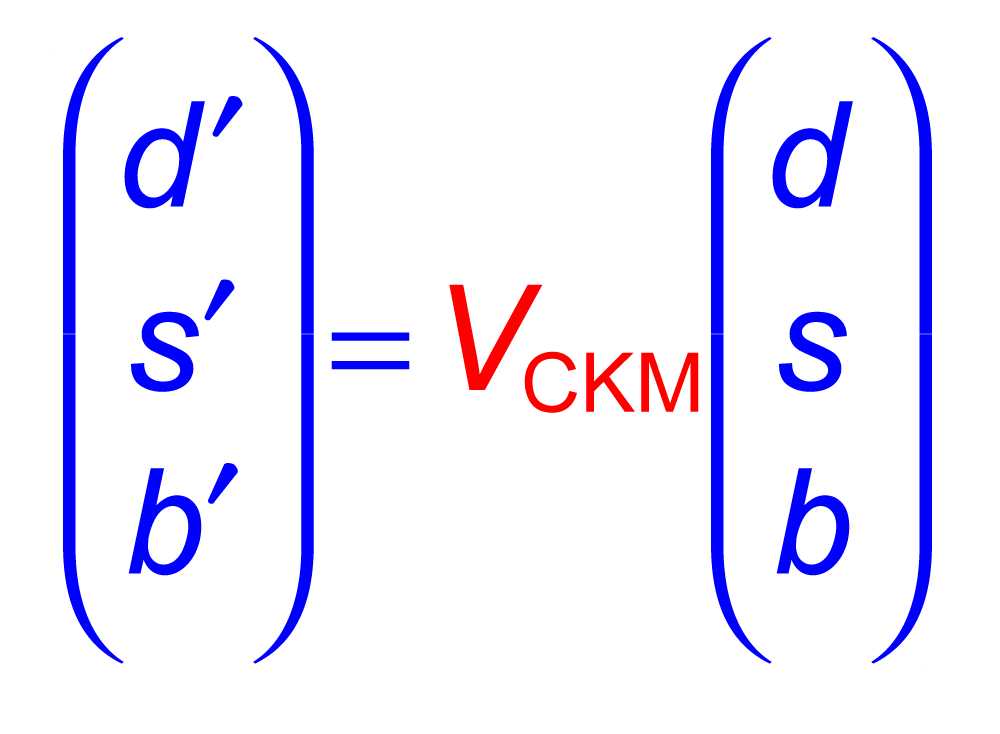
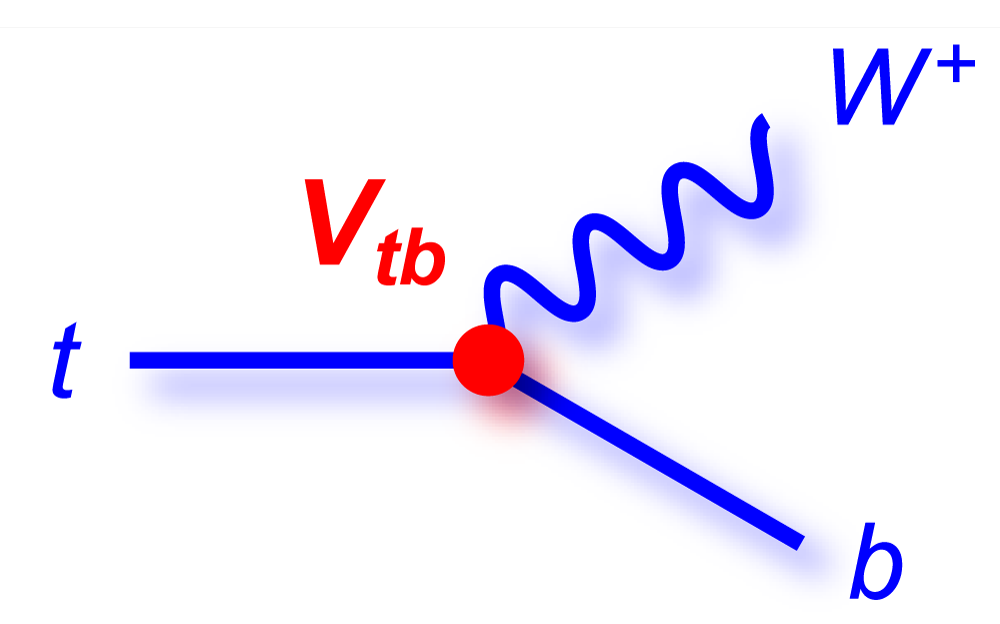
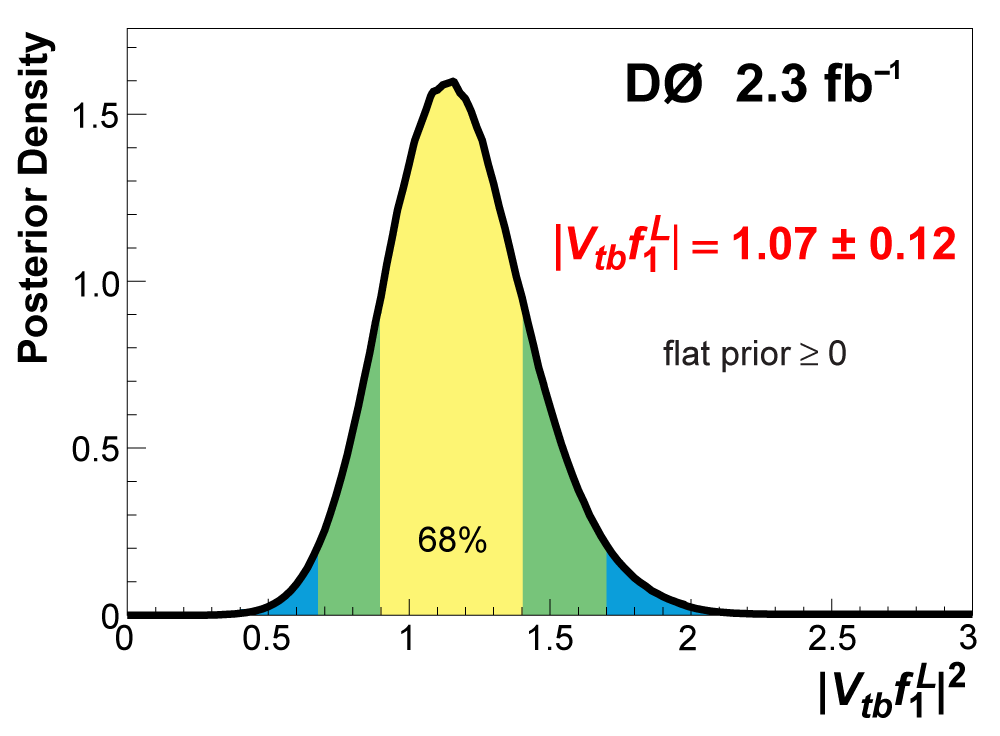
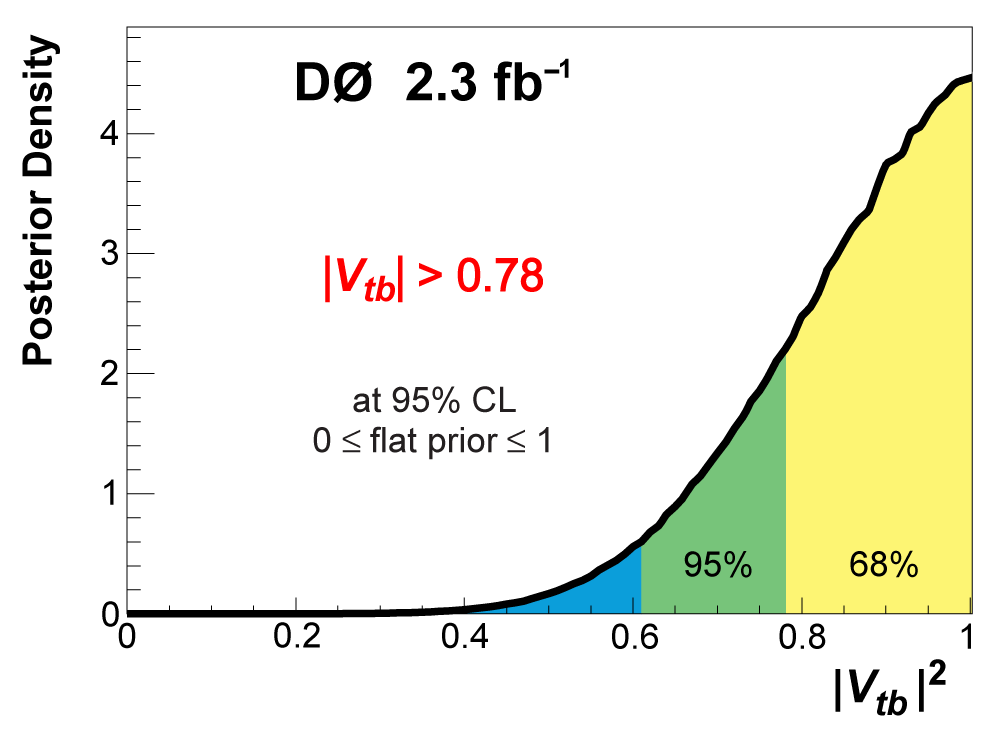
| The Cabibbo-Kobayashi-Maskawa matrix describes the mixing between quarks to get from the strong-interaction eigenstates to the weak-interaction ones. The term relating top quarks to bottom quarks is known as Vtb. The single top quark production cross section is proportional to |Vtb|2 and can thus be used to measure the amplitude of Vtb. To make this measurement, we assume the standard model for top quark decay (i.e., mostly to Wb and not much to Wd or Ws), and that the Wtb coupling is left-handed and CP-conserving. We do not assume there are exactly three quark generations for this measurement. The following two plots show our results, first for when the strength of the left-handed scalar coupling f1L is not constrained, and second for when it is set equal to one. |
 |
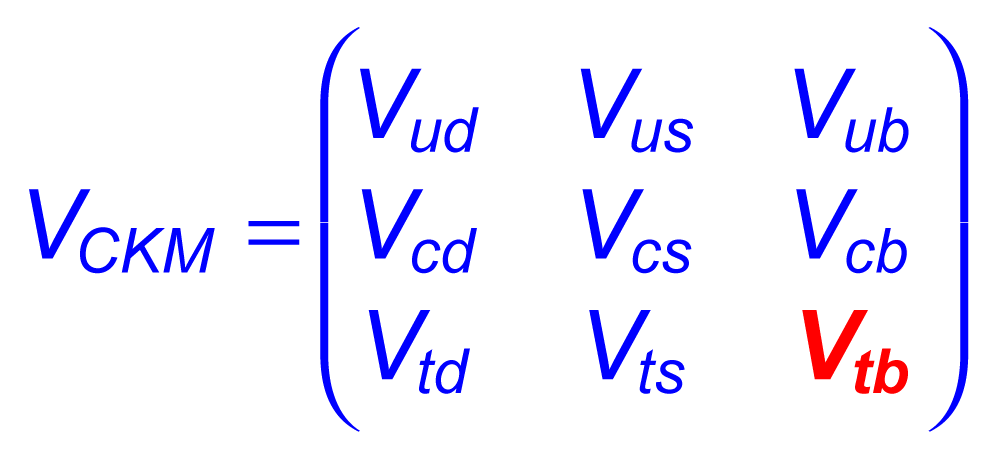 |
 |
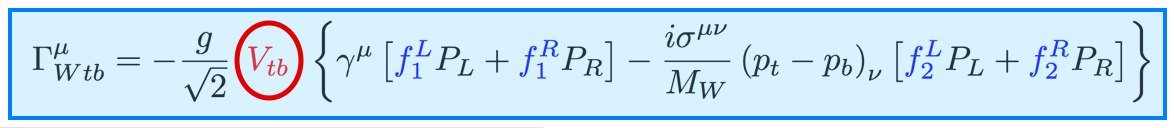 |
 |
 |
 |
 |
 |
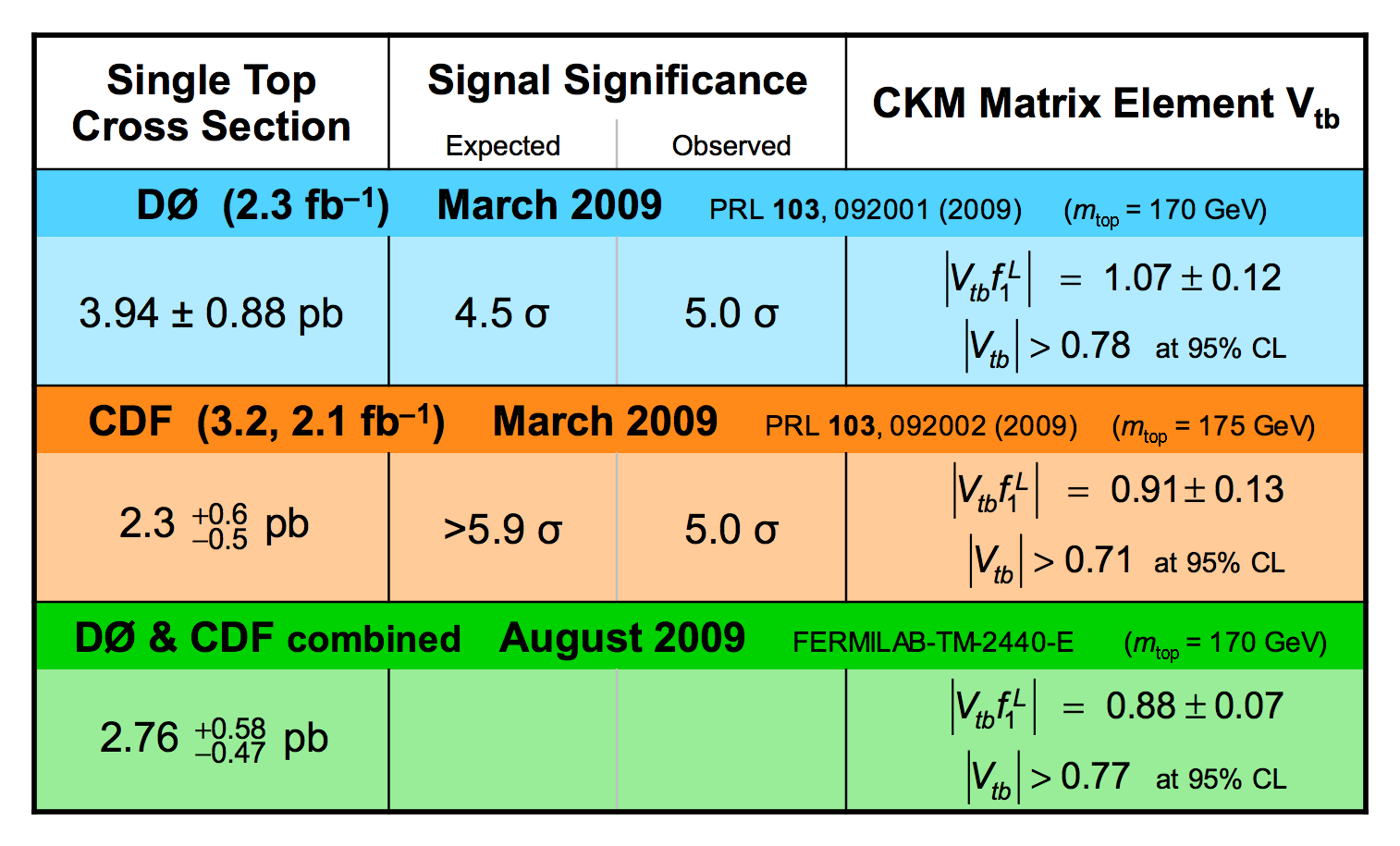
| Because the uncertainty of ±0.12 on the result |Vtbf1L| = 1.07 ± 0.12 is determined from the width of the posterior density distribution, as shown in the left-hand plot above, it includes all components: statistics, systematics, and theory. |
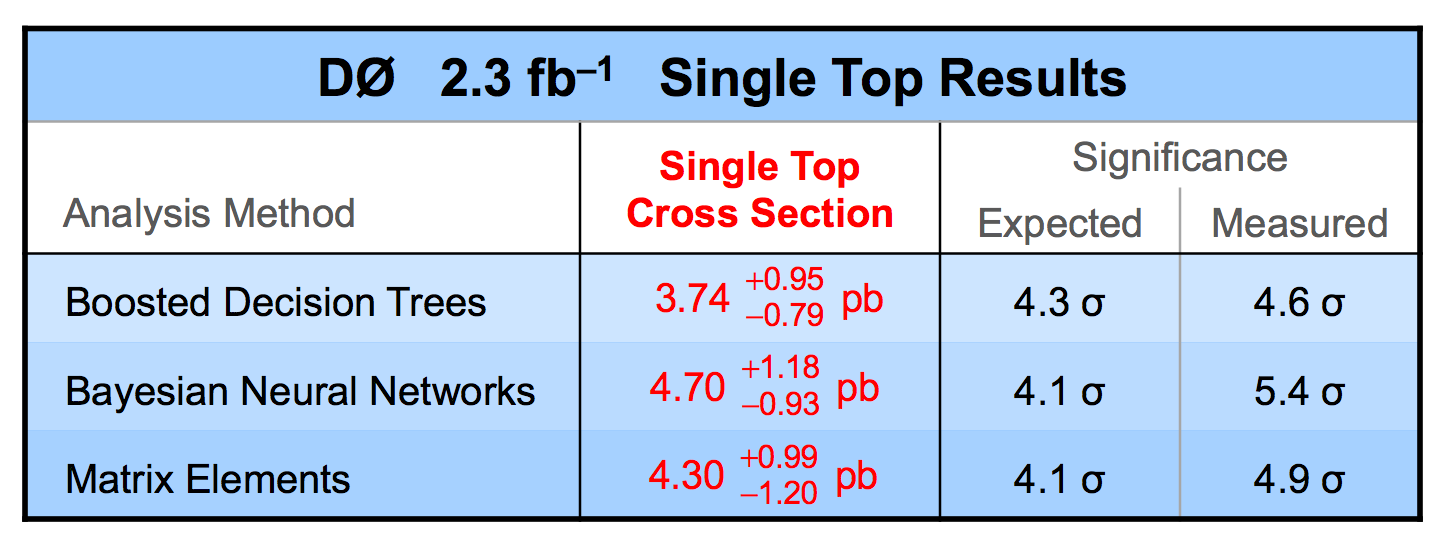
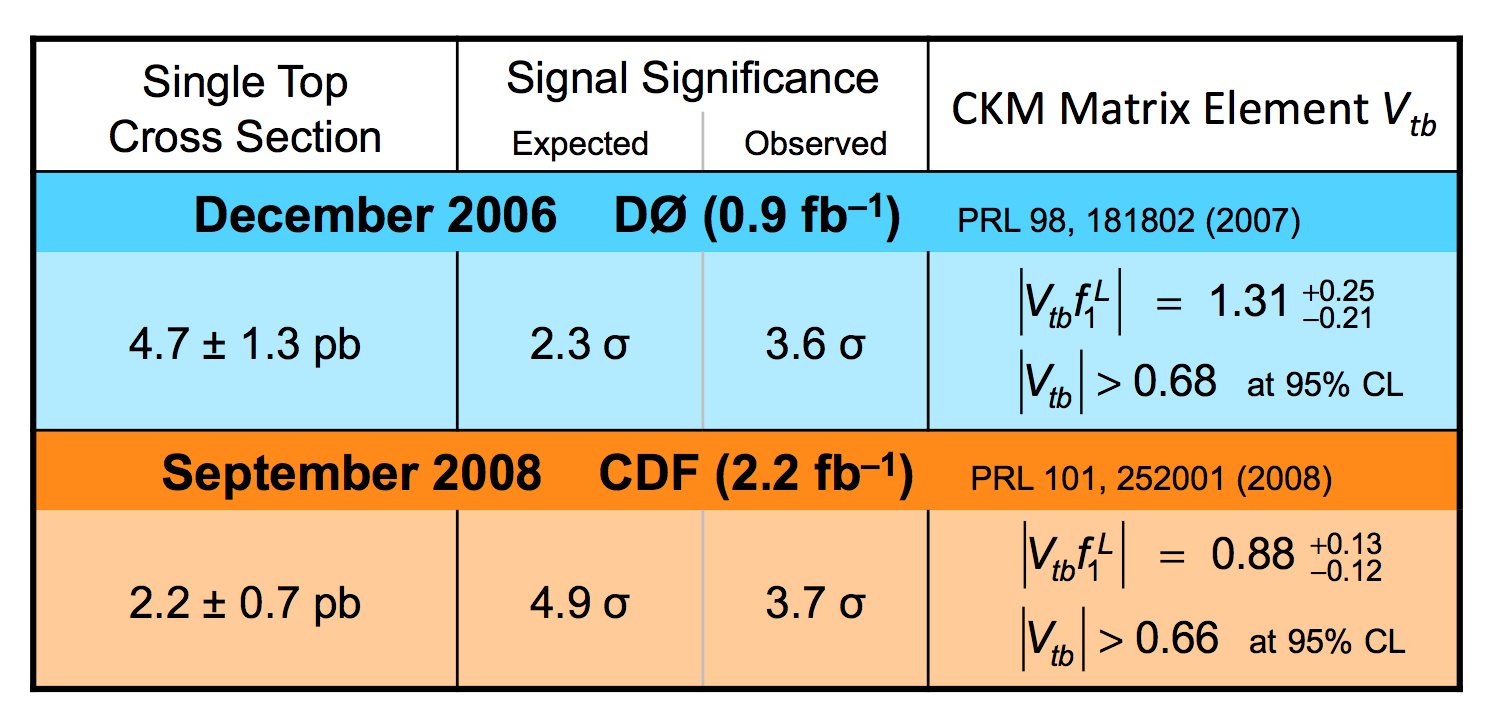
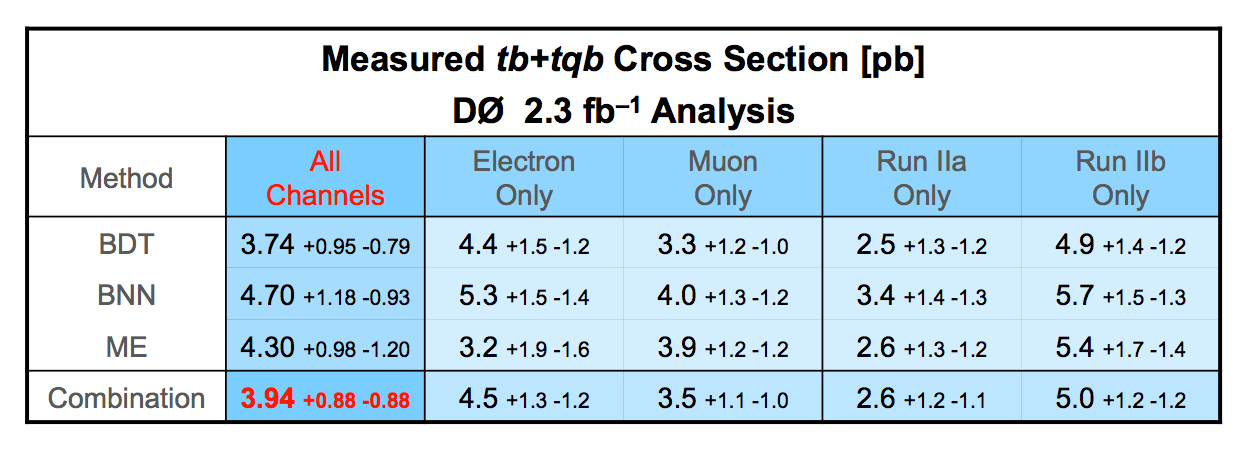
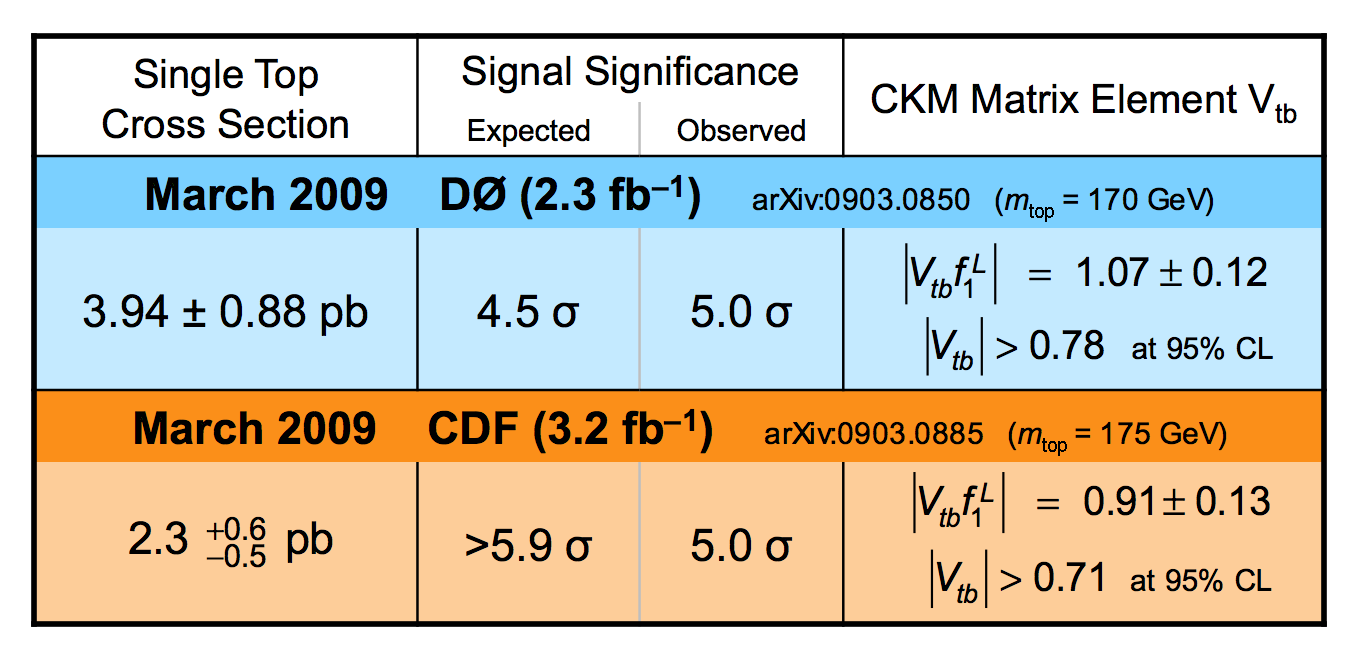
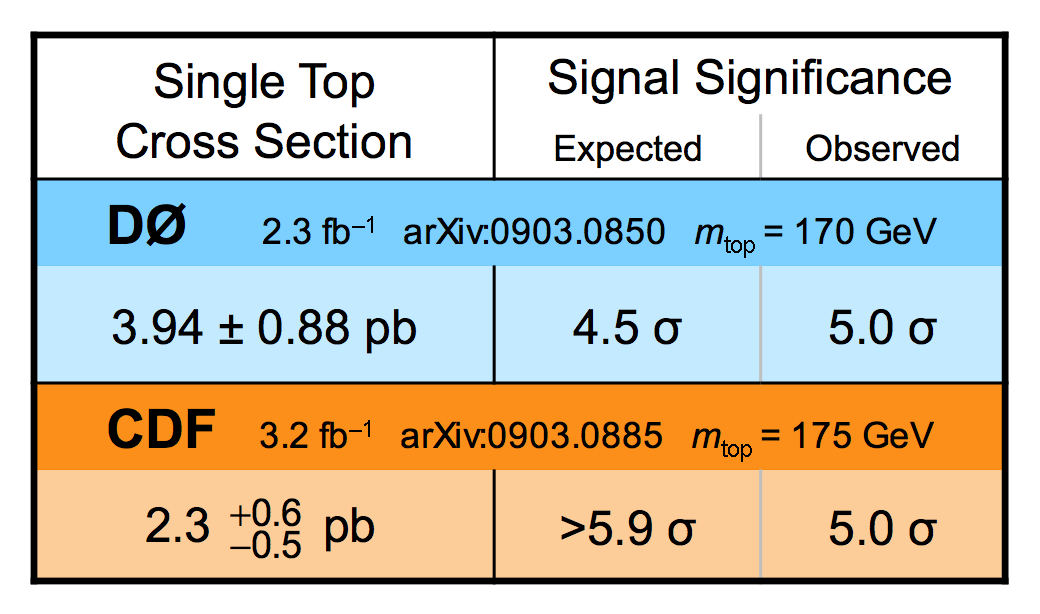
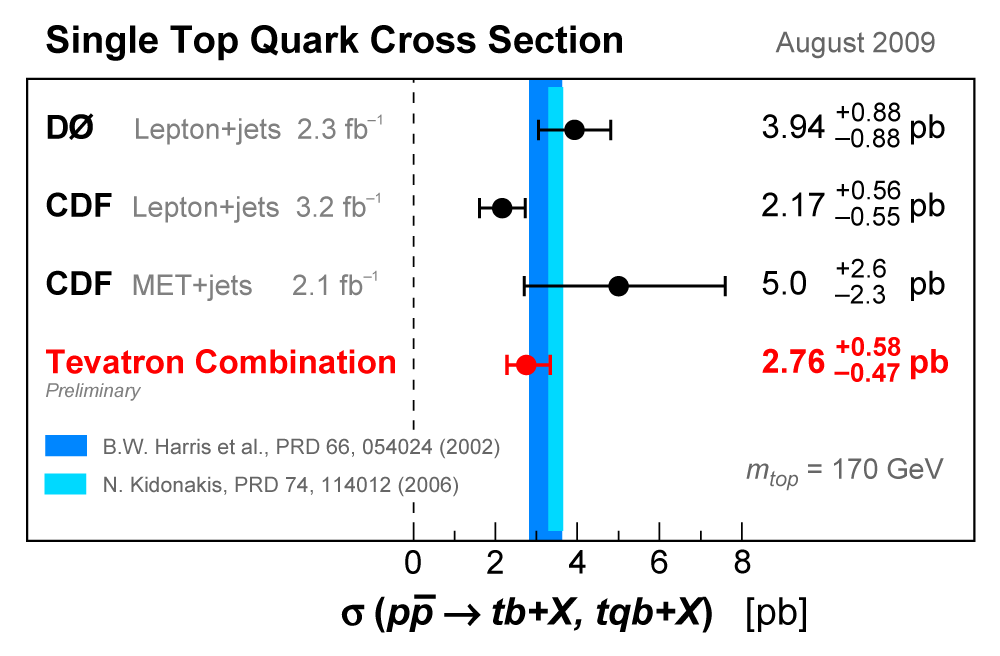
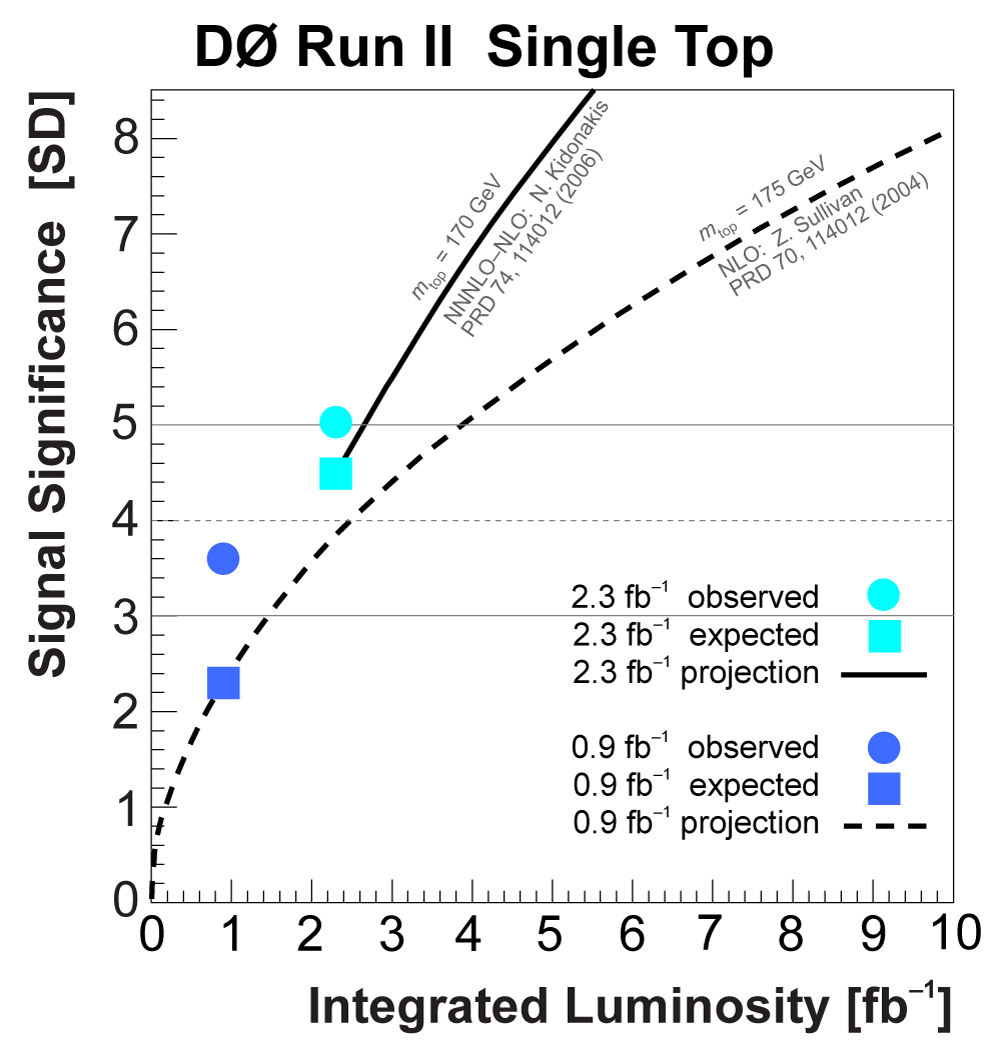
| We have measured the single top quark production cross section using 2.3 fb-1 of data at the DØ experiment. The cross section for the combined tb+tqb channels is 3.94 ± 0.88 pb. Our result provides an improved direct measurement of the amplitude of the CKM quark mixing matrix element Vtb. The measured single top quark signal corresponds to an excess over the predicted background with a p-value of 2.5 × 10-7, which is equivalent to a significance of 5.0 standard deviations – this is the first observation of single top quark production. |
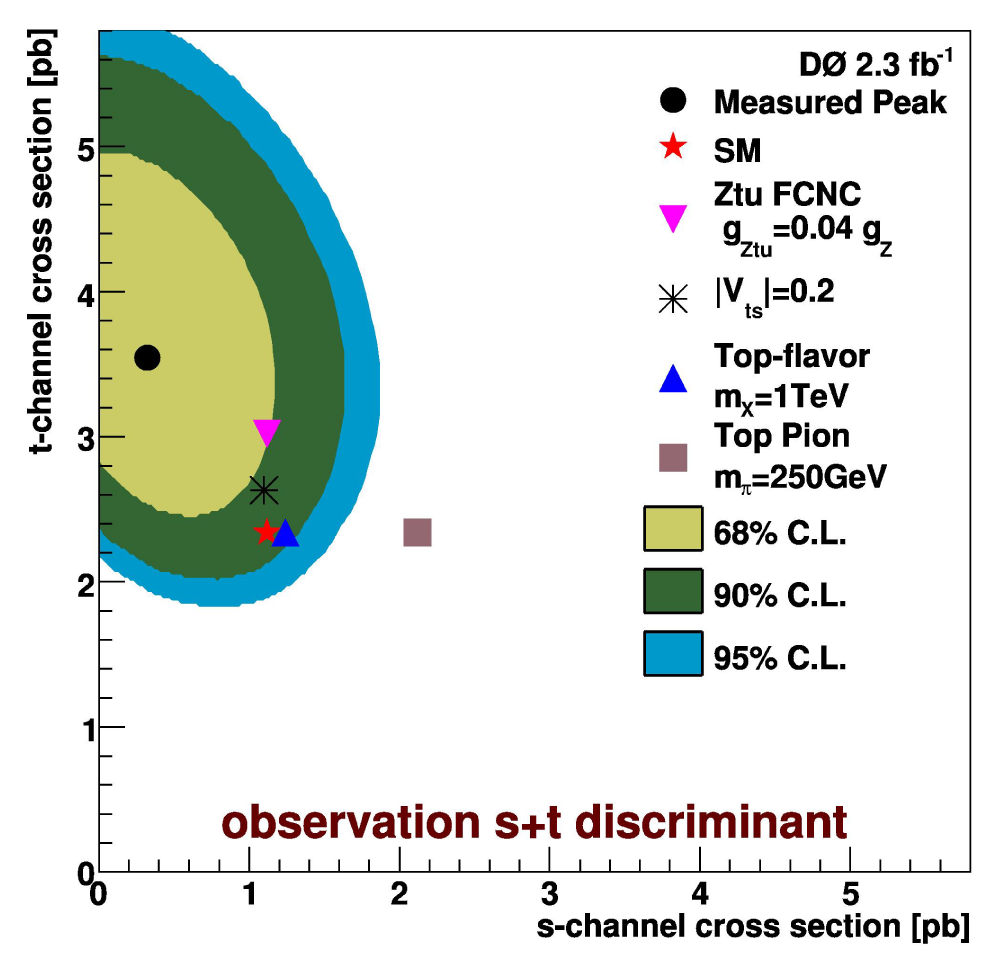
 |
The following plots shows the posterior probability density using the final s+t channel discriminant from this analysis, as
a function of the t-channel and s-channel cross sections in contours of equal probability density. Also shown are the measured
cross section, SM expectation, and several representative new physics scenarios:
|
 |
| • Les Rencontres de Physique de la Vallée d'Aoste | DØ & CDF results | Gustavo Otero y Garzon, Universidad de Buenos Aires | March 2009 |
| • Fermilab Joint Experimental-Theoretical Seminar | DØ results | Cecilia Gerber, University of Illinois, Chicago | March 2009 |
| • Rencontres de Moriond: QCD and Hadronic Interactions | DØ & CDF results | Dag Gillberg, Simon Fraser University | March 2009 |
| • HEP seminar, SLAC | DØ results | Meenakshi Narain, Brown University | March 2009 |
| • American Physical Society April Meeting, Denver | Poster of DØ results | Ann Heinson, Cecilia Gerber, Reinhard Schwienhorst | May 2009 |
| • American Physical Society April Meeting | DØ & CDF results | Lisa Shabalina, Georg-August-Universität Göttingen | May 2009 |
| • American Physical Society April Meeting | DØ BDT result | Ann Heinson, University of California, Riverside | May 2009 |
| • American Physical Society April Meeting | DØ ME result | Monica Pangilinan, Brown University | May 2009 |
| • American Physical Society April Meeting | DØ BNN result | Cecilia Gerber, University of Illinois, Chicago | May 2009 |
| • Madison Phenomenology Symposium | DØ results | Monica Pangilinan, Brown University | May 2009 |
| • HEP seminar, Brookhaven | DØ results | Shabnam Jabeen, Boston University | May 2009 |
| • HEP seminar, Bern | DØ results | Reinhard Schwienhorst, Michigan State University | May 2009 |
| • International Conference on Supersymmetry, Boston | DØ results | Liang Li, University of California, Riverside | June 2009 |
| • Rencontres de Blois: Windows on the Universe | DØ & CDF results | Ann Heinson, University of California, Riverside | June 2009 |
| • Europhysics Conference on HEP, Krakow | DØ results | Reinhard Schwienhorst, Michigan State University | July 2009 |
| • APS Division of Particles and Fields Meeting, Detroit | DØ results | Cecilia Gerber, University of Illinois, Chicago | July 2009 |
Reports
|
Press releases |
 |
 |
 |
 |
 |
 |
 |
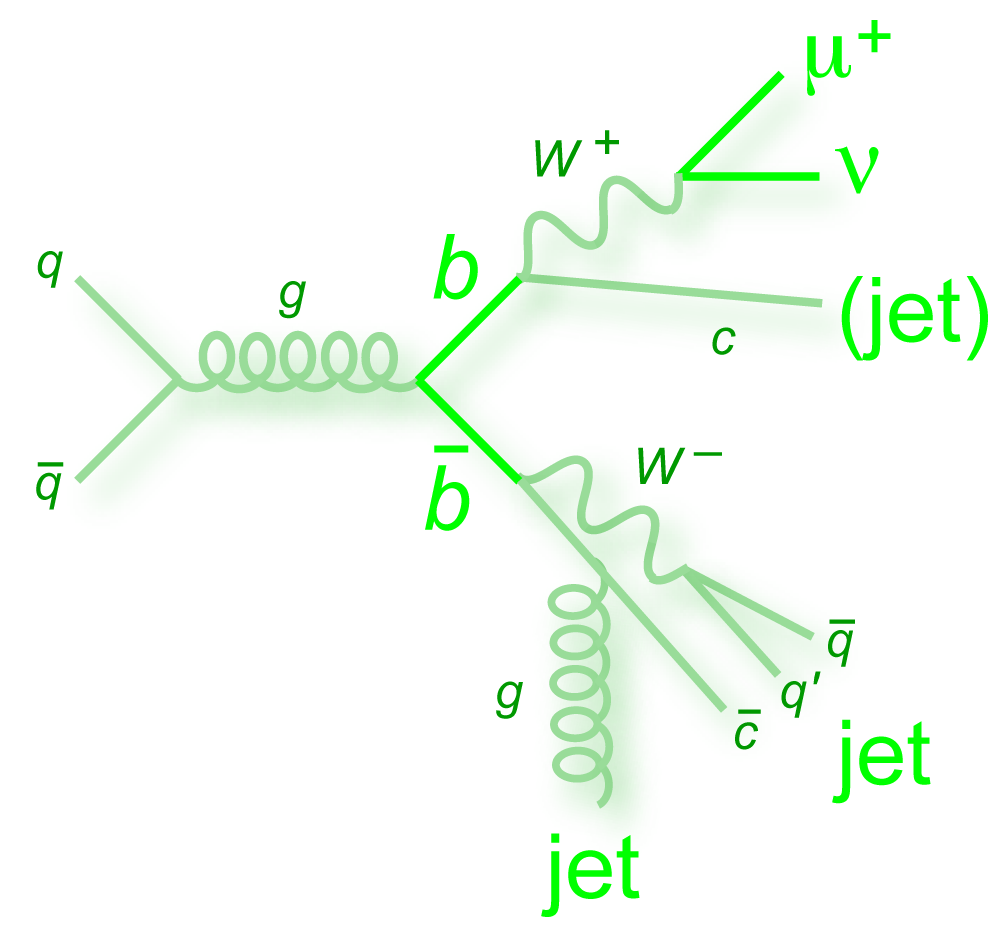 |
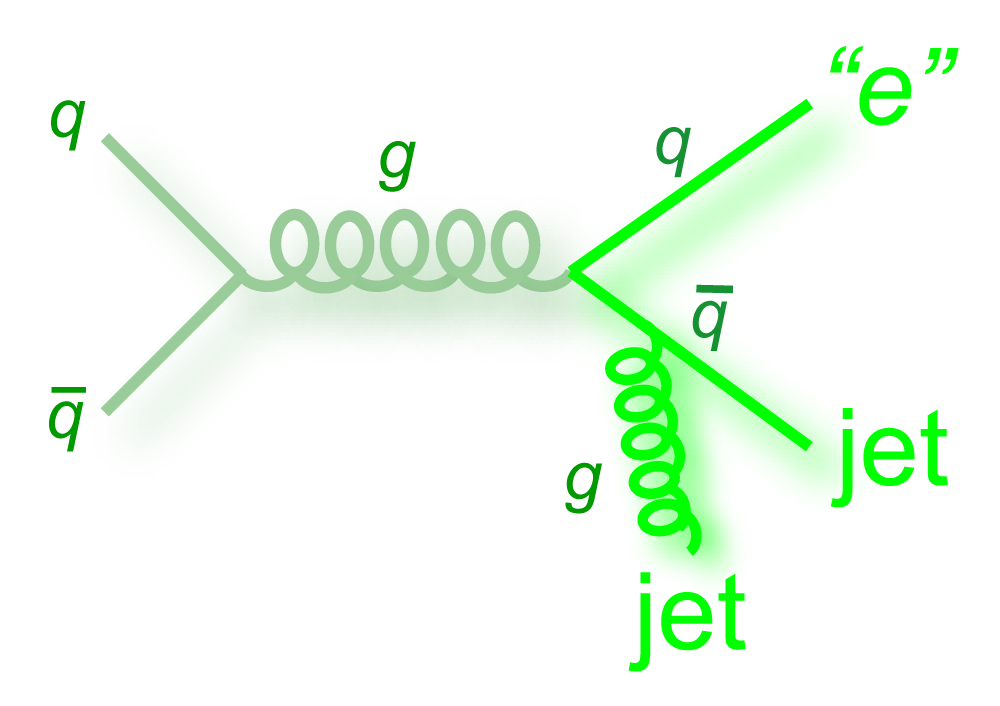 |
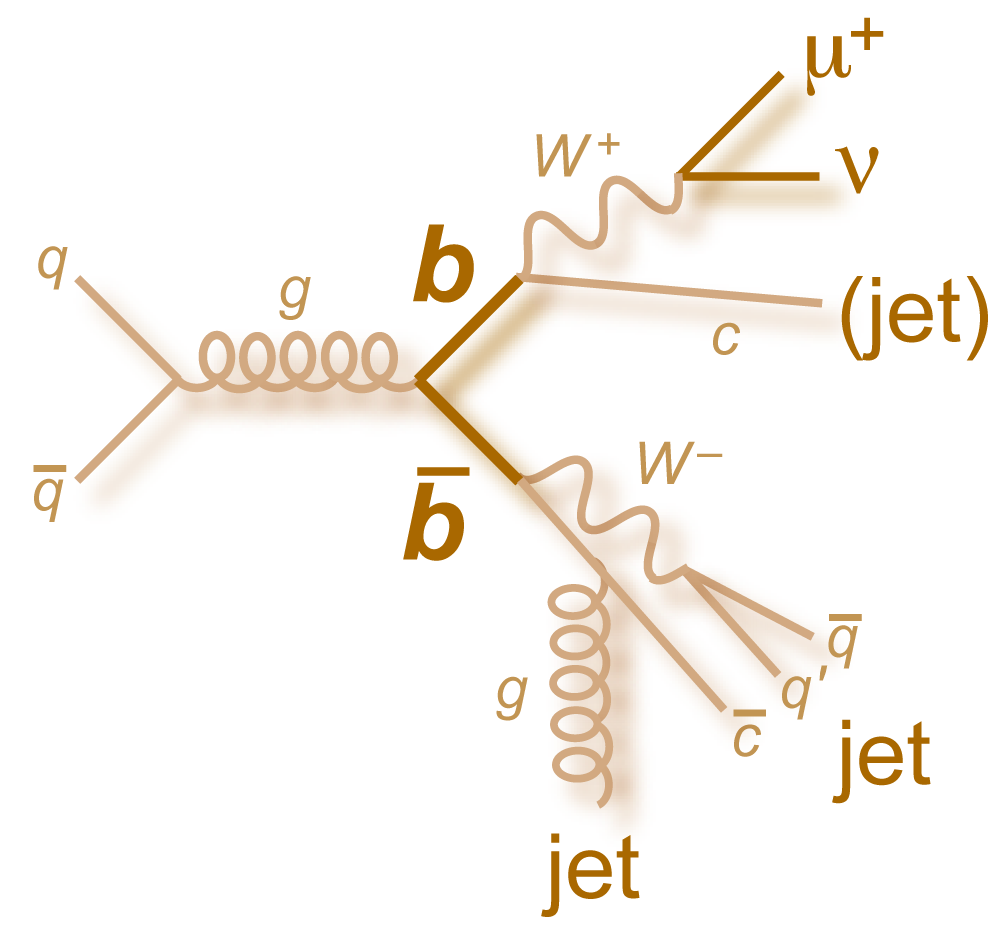 |
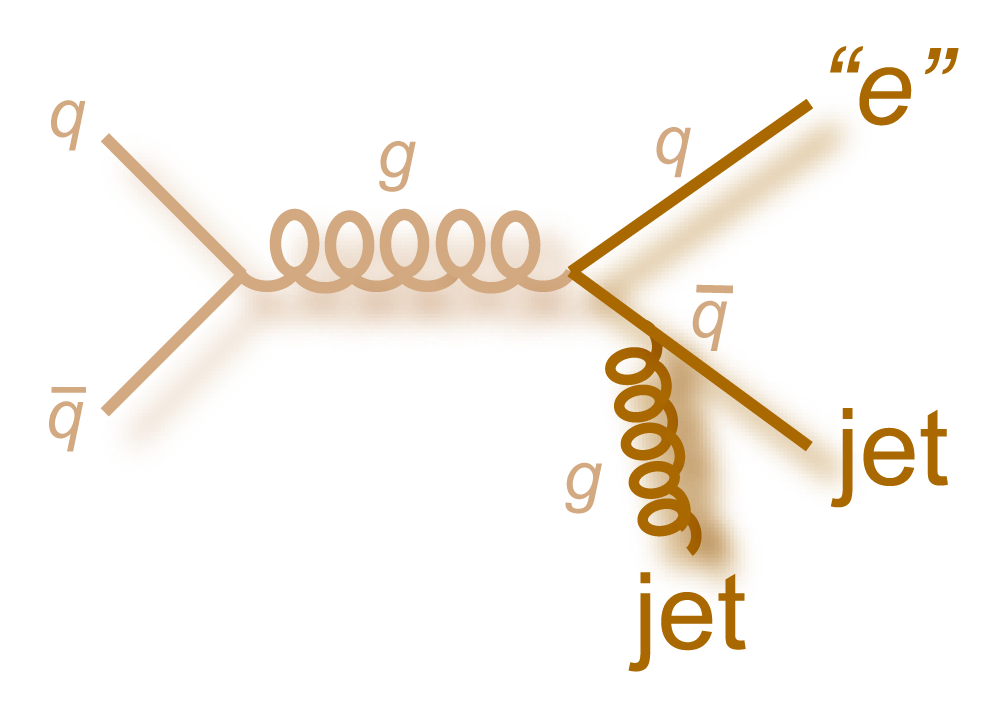 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
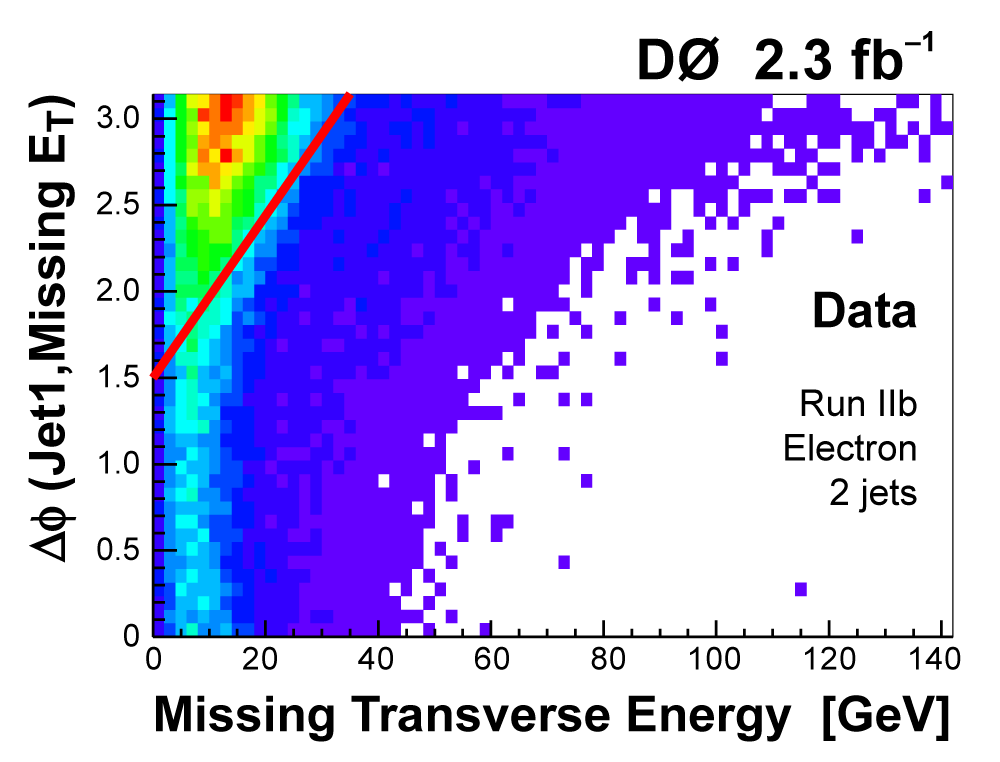
 |
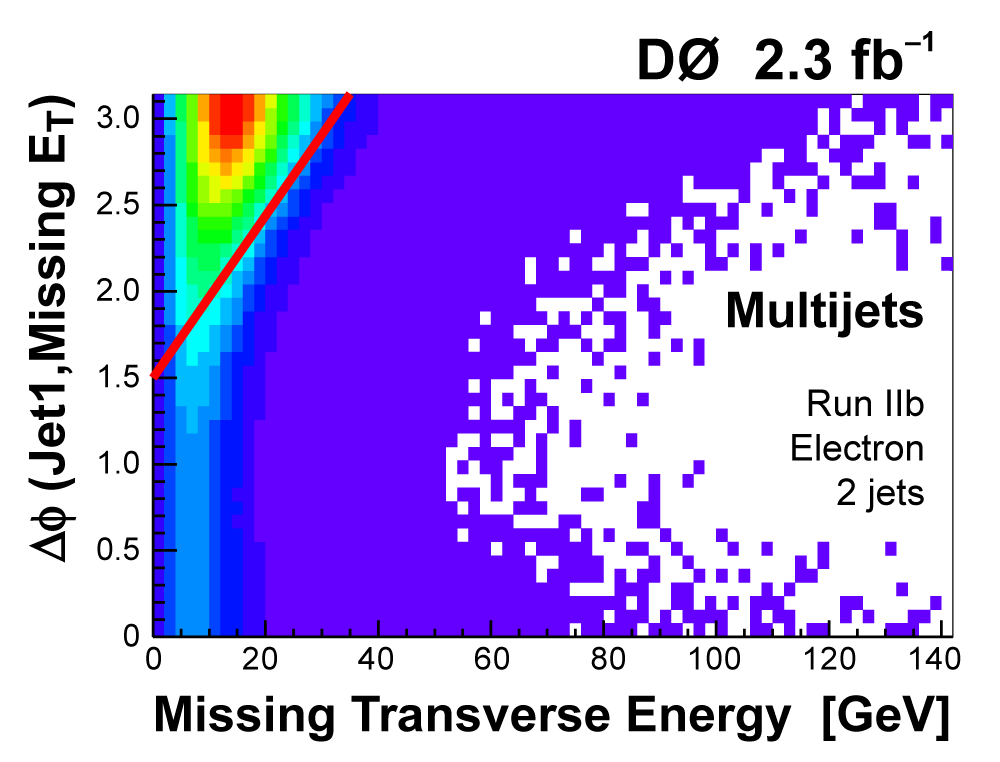
 |
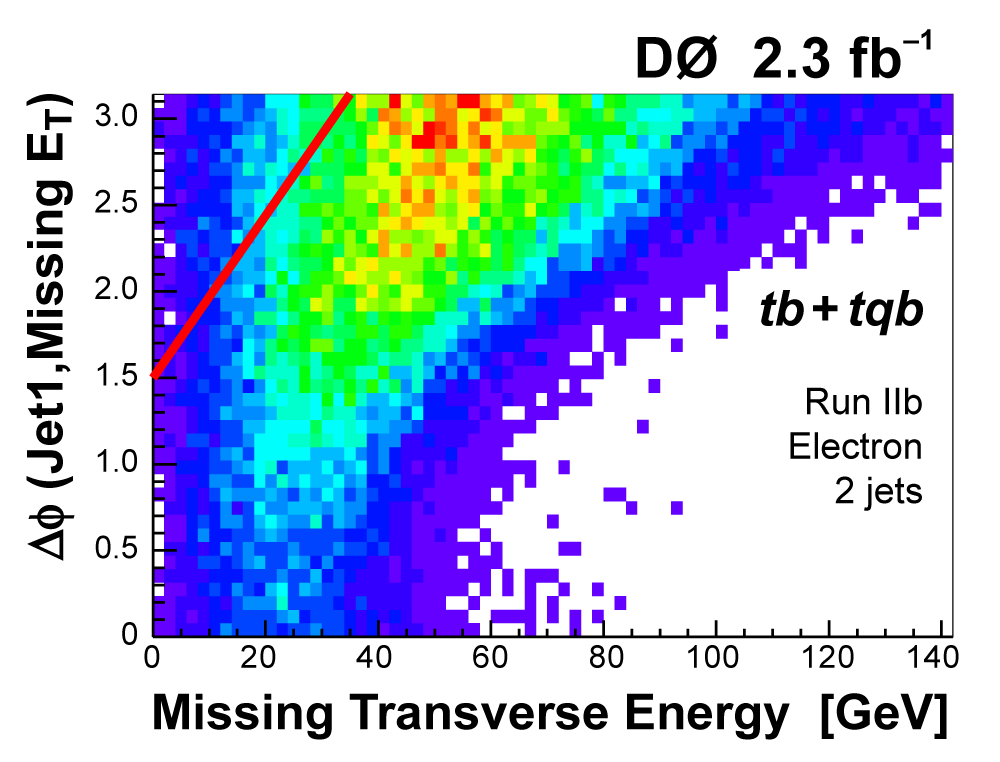
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |  |
 |
 |
 |
 |
 |
 |
 |
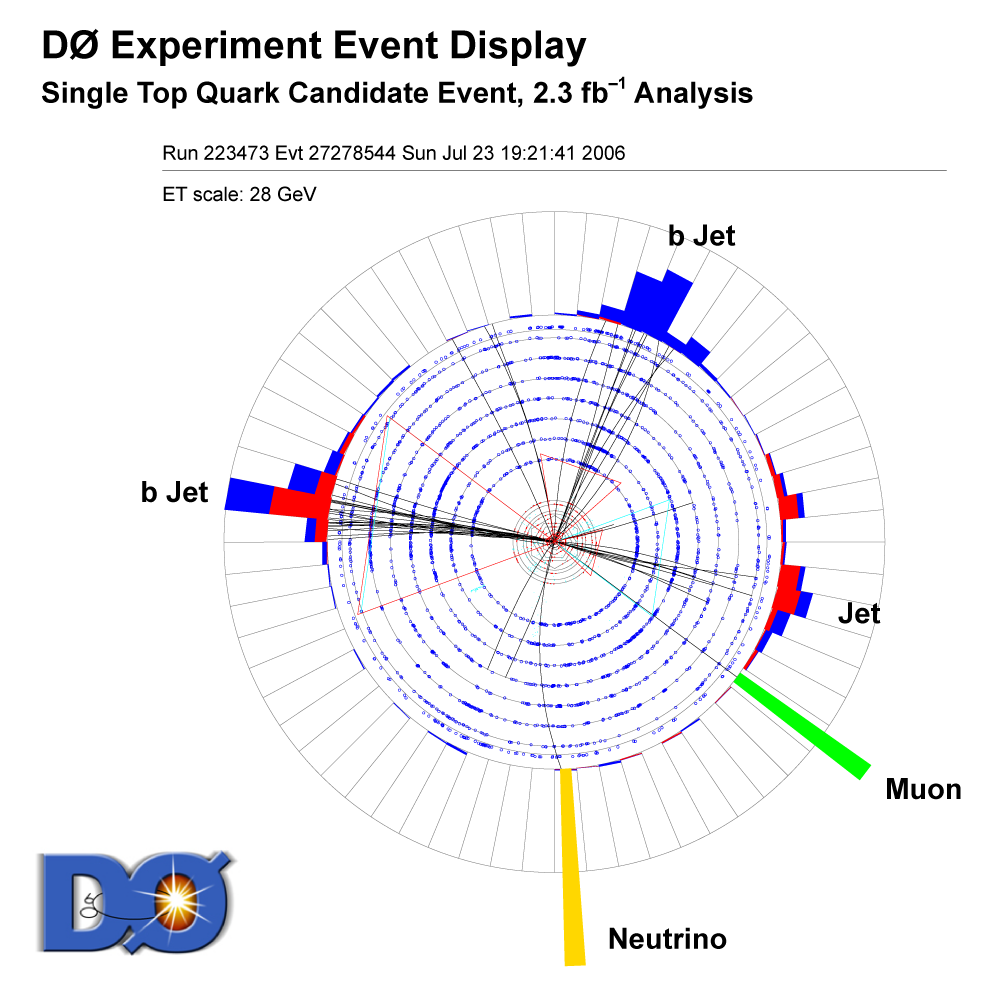 |
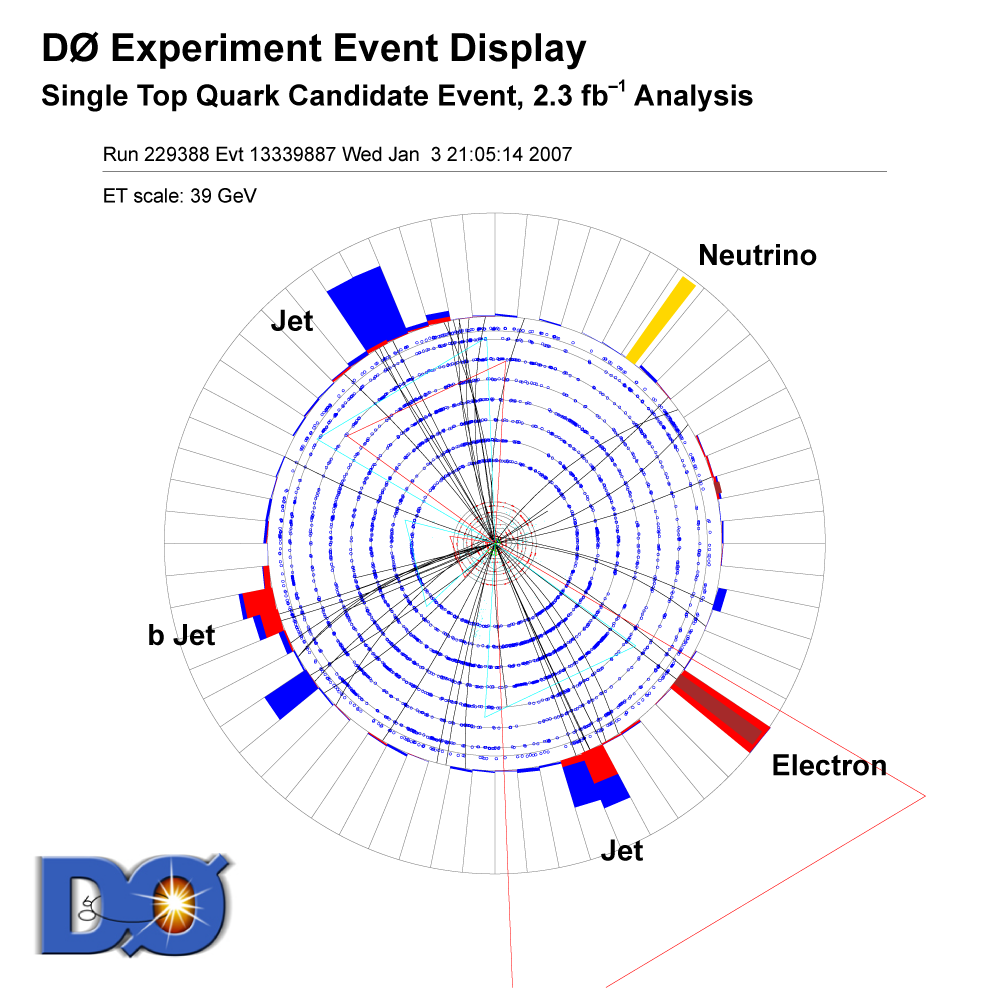 |
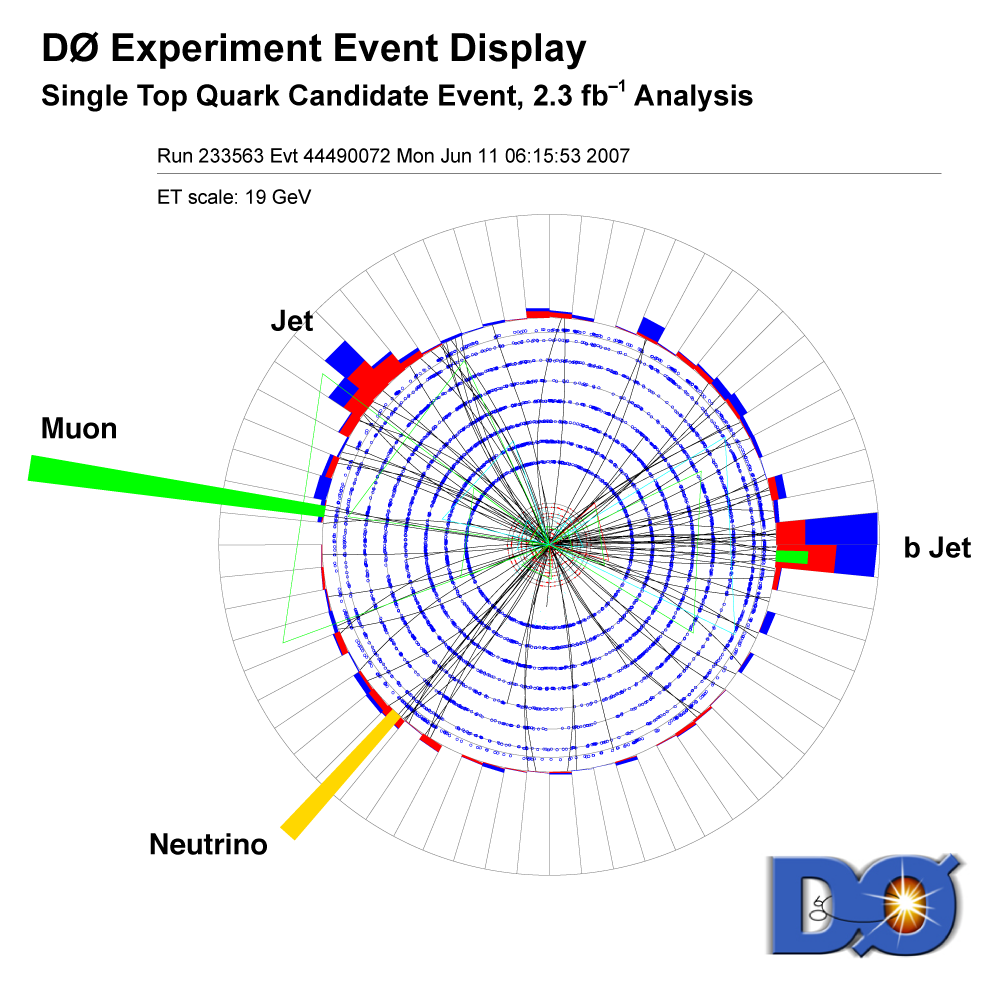 |
 |
 |
 |
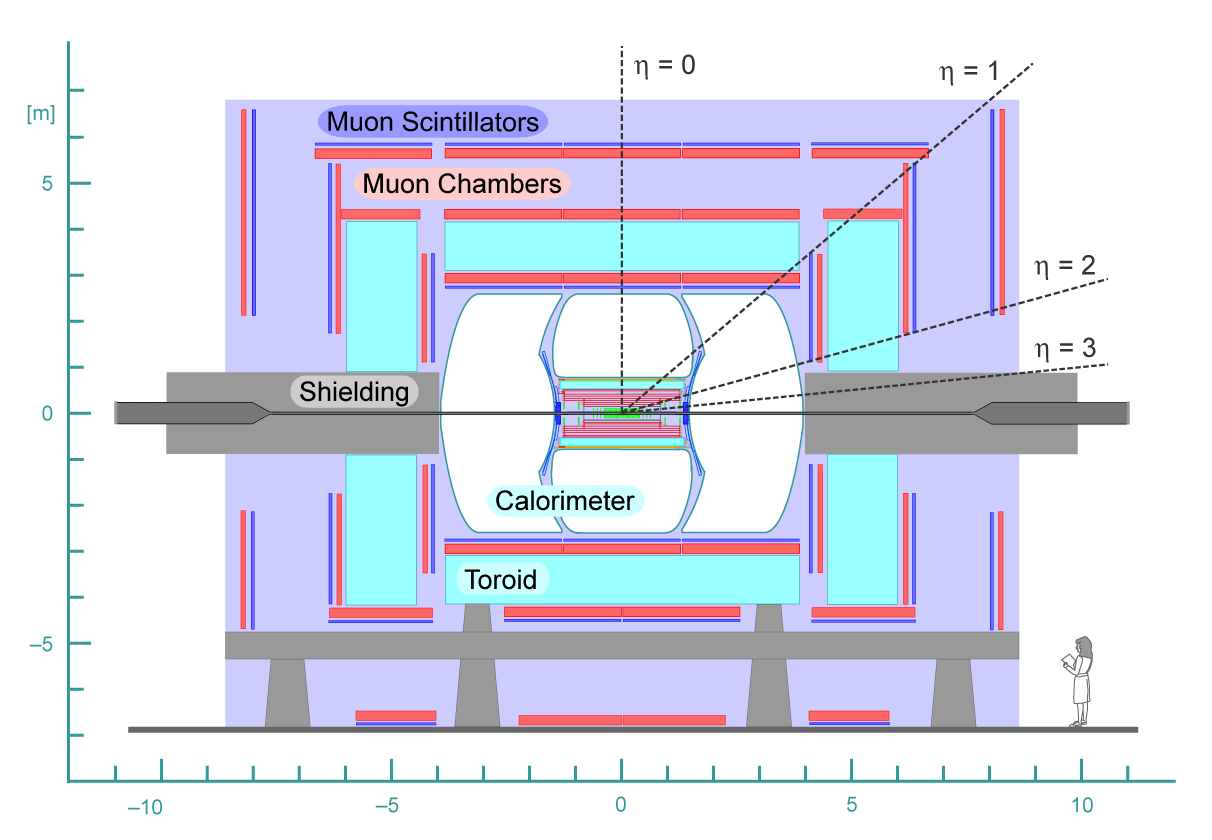 |
 |
 |