
the full paper by the D0 Collaboration can be found here
The top quark is the most massive of the six known quarks. The two lightest quarks, up and down, make up the protons and neutrons in the nuclei of atoms. The more massive quarks quarks have similar properties as the up and down quarks but they are unstable and ultimately decay to the lightest quarks. The value of the top quark mass affects certain observables, such as the W boson mass and the Higgs boson mass. In order to make precise comparisons of these observables to theoretical predictions the top quark mass must be known precisely.
Most top quarks at the Tevatron are produced along with their antiparticle, the antitop quark. The top quark decays to the next lighter quark, the bottom quark, by emitting a positively charged W boson and the antitop quark decays to an antibottom quark by emitting a negatively charged W boson. The bottom and antibottom quarks turn into collimated sprays of particles, called jets, that we detect in our detector. We measure their energy and direction. The W bosons decay a small fraction of the time to a lepton, such as an electron or a muon, that carries the same charge as the W boson and a neutrino. Charged leptons are detected and measured in our detector but neutrinos escape unseen. When both W bosons from the top and antitop quarks decay in this way we get events in which two jets from the bottom and antibottom quarks and two charged leptons are observed in the detector. The undetected neutrinos carry away momentum. We can infer this missing momentum by adding up the momenta of all observed particles in the event. We call such events dilepton events.
We detect a total of 26 events with two identified leptons in our data from an integrated luminosity of 370 pb-1. There are an additional 9 events in which one lepton is only observed by the trace it leaves in the innermost part of our detector, which measures the trajectories of charged particles. Not all of these events are from the decay of top and antitop quarks. There are other processes that give rise to similar signatures. These are called backgrounds. We have performed two analyses to determine the mass of the top quark from these events. These two analyses differ in a number of ways.
The first difference is in the treatment of the event samples. Analysis A uses only the events with two identified leptons. It divides these into two groups. For events in the "b-tag" sample at least one of the jets from the bottom quarks is uniquely identified as originating from a bottom quark. This reduces the number of background events essentially to zero because the background processes do not involve bottom quarks. The remaining events in which none of the jets could be identified in this way comprise the "no-tag" sample. Analysis B does not distinguish between these two classes of events but applies slightly tighter requirements to reduce backgrounds. We call this the "tight" sample. The second method also uses the events with only one identified lepton, which we call the "lepton+track" sample.. Table 1 gives the number of events expected from backgrounds and from top/antitop quark decays and the number of events detected in the data for all these samples.
Table 1: number of events expected from top/antitop quark decays and backgrounds and number of events observed in the different event samples
| sample | top/antitop | backgrounds | total | data |
| b-tag | 9.9 | 0.2 | 10.1±0.9 | 14 |
| no-tag | 7.2 | 6.0 | 13.2+2.8-2.1 | 12 |
| tight | 15.8 | 4.0 | 19.8±0.6 | 21 |
| lepton+track | 6.3 | 2.2 | 8.5±0.3 | 9 |
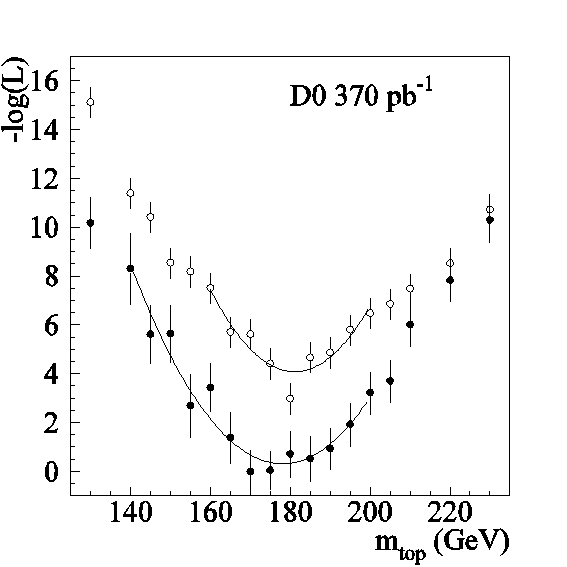
The mass of a particle can be reconstructed from the measured momenta of the particles it decays into. With our dilepton events we face several complications that prevent us from doing this. Most importantly, the neutrinos from the decay are not detected and this their momenta are unknown. This leaves us with too little information to reconstruct the mass of the decaying top or antitop quark. In addition it is not possible to determine which jet came from the decay of the top quark and which came from the decay of the antitop quark. To make matters worse there are sometimes additional jets in the event that do not originate from either top quark or antitop quark decay. Since we cannot reconstruct the mass of the top quark or antitop quark directly, we compute the probability that the event would be produced as a function of the top quark mass. We call this the event weight function. In analysis A we simply take the top mass at which this the event weight function is largest (peak mass) and compare its distribution to that from simulated events with different assumptions about the top quark mass. Figure 1 shows the distribution of the peak mass for the data and for simulated events, assuming the top quark mass is 180 GeV. We find that the best match between data distribution and simulation occurs if the top quark mass is assumed to 176 GeV. In analysis B the shape of the event weight function is also considered in the comparison with the simulation. Here we find that the best match occurs for an assumed top quark mass of 180 GeV. Figure 2 shows the negative logarithm of the likelihood that simulation and data agree versus top quark mass for both analyses. The best match occurs when this quantity reaches its smallest value.
|
|
|
| Figure 1: negative logarithm of likelihood for comparison of data and simulation versus the top quark mass assumed in the simulation. | Figure 2: distribution of peak masses for dilepton events (points), simulation with top quark mass = 180 GeV (open histogram) and backgrounds (shaded histogram). |
We combine the results of both analyses, taking into account their correlations, and find a best estimate of the top quark mass of 178.1 GeV. The uncertainty from fluctuations due to the finite sample of events, which is called the statistical uncertainty, is 6.7 GeV. If we could repeat our experiment and measure the top quark mass from another random set with the same number of dilepton events, this is how much we would expect the result to vary on average.
Finally we study how this result changes as various assumptions are varied. To do this we use our simulation to generate samples of dilepton events that we processes like the data events to "measure" a top quark mass. We change the assumptions in the simulation and observe the resulting change in the measured top quark mass. We find that the most important effect originates from the calibration of the energy measurement of the jets. This calibration is known to a precision of 4.1%. We vary it by this much and observe a variation of the combined measured top quark mass by 4.3 GeV. This uncertainty in our result is called a systematic uncertainty. The effect of other systematic uncertainties is tabulated in Table 2. We add these uncertainties by computing the square root of the sum of the squares of the uncertainties. This accounts for the fact that we are not likely to be off in all assumptions by the maximum amount. The result is a total systematic uncertainty of 4.8 GeV.
Table 2: summary of systematic uncertainties
| source | uncertainty |
| jet energy calibration | 4.3 GeV |
| structure of the proton | 0.8 GeV |
| simulation of additional jets | 1.5 GeV |
| understanding of backgrounds | 0.9 GeV |
| simulation statistics | 0.9 GeV |
| detector resolution | 0.4 GeV |
The top quark mass has been measured by the D0 and CDF experiments using a number of different methods and in different types of top quark decays. The world average of all previous such measurements is 172.5 ± 2.3 GeV. Our result is in good agreement with this number.
In conclusion, we measure the top quark mass to be 178.1 ± 6.7(statistical) ± 4.8(systematic) GeV using dilepton decays of top-antitop quark pairs.