Search for R-parity Violating Supersymmetry via the LLE Couplings
λ121, λ122 or λ133 in Proton-Antiproton Collisions (full paper)

 

  Preface: What are we doing in general?

Particle physics is dedicated to the study of the fundamental building blocks of matter and tries to explain how they bind together to form atoms, molecules and so on. The goal is to describe everything with the simplest possible theory. A large number of experiments was and is conducted to improve our knowledge, and over many years of active research, the so-called Standard Model (SM) of particle physics has emerged. This very successfull theory describes three of the four fundamental interactions: electromagnetic, weak, and strong. The fourth one, gravity, is too weak to be measureable in particle interactions. Hence, gravity is so far ignored in the Standard Model, but will have to be included some time in the future, because otherwise interactions at very high energies cannot be described correctly. According to the SM, three families of leptons and quarks exist and interact via the aforementioned forces. Quarks and leptons are spin-1/2 particles, called fermions. They define the matter fields and interact by exchanging integer-spin bosons, which are sometimes also called force carrier particles. For example, the W± and Z0 bosons and the photon γ are the force carriers of the electroweak interaction, which combines electromagnetism and the weak interaction.

Even though we have learned a lot over the past decades, we are unfortunately still pretty far away from the one (simple) theory to describe and explain each and everything, the sought-after Theory Of Everything, or how we usually call it: the grand unified theory (GUT). Among many possible candidate theories, supersymmetry (SUSY) represents a very promising approach. SUSY not only addresses many of the problems that still persist in the SM, but also offers a possibility to unify all four interactions, including gravity.

 

  R-parity Violating Supersymmetry – What in the world is this?

SUSY predicts the existence of a partner particle for each SM particle, differing only by half a unit in spin, but otherwise sharing the same quantum numbers. Fermions, spin-1/2 particles (leptons & quarks) are assigned bosonic partners with spin-0, called sleptons and squarks. For instance, the superpartner of an electron is a selectron, for a muon a smuon, and so on. Spin-0 particles are also called scalar particles, explaining the origin of the "s" in front of the Standard Model particle's name. On the other hand, all of the SM gauge bosons (W± and Z0 bosons and the photon γ) and the Higgs bosons (five particles as opposed to one in the SM) have fermionic partners. These form - yet to be discovered - observable massive particles, called neutralinos and charginos. All leptons / sleptons carry a lepton quantum number L, while all baryons (quarks/squarks) carry a baryon quantum number B. The lepton, baryon and spin quantum numbers of the (s)particles are connected via R-parity:
                    Rp = (-1)3B+L+2S      ordinary particles always have:   Rp = +1
                                                     and SUSYparticles always have:   Rp = -1.
Two different types of SUSY models have to be distinguished: models, which respect R-parity and conserve B and L, i.e. R-parity conserving SUSY (RPC-SUSY), and models, which violate either B or L, called R-parity violating SUSY (RPV-SUSY) in the following. In the former, the lightest supersymmetric particle (LSP) is stable since a decay in SM particles would violate either L or B. In case the LSP is electrically neutral, it would provide a nice dark matter candidate. The latter models do not offer such a candidate, as supersymmetric particles are allowed to decay into SM particles and no heavy stable particle is left anymore. However, RPV-SUSY may well be what is realized in nature and sets the stage for our analyses.
R-parity violation can be separated into interactions violating either L or B conservation. Since this analysis is solely concerned with lepton number violation, it deals only with the following LLE-term:     λijkLiLjEk
This term describes the interaction of one slepton superfield with two ordinary lepton superfields. More exactly, the two L denote (s)lepton weak isospin doublet superfields (left-handed e,µ,τ, and ν's) and E stands for one right-handed singlet superfield (e,µ,τ). The indices i,j,k refer to the three fermion families and the interaction strength is given by the value of the respective Yukawa coupling λijk. The results are interpreted in two RPV-SUSY models: in the minimal supergravity model (mSUGRA) and a Minimal Supersymmetric Standard Model without GUT-relation between the masses M1 and M2 of the partner sparticles of the U(1) and SU(2) gauge bosons (this model is called no-GUT MSSM). In both models the lightest neutralino is assumed to be the LSP.

fig1
The Feynman diagrams of two LSP-decays (eps)
via the LLE-term.

 

  Searching for RPV-SUSY at the Tevatron

Due to the Proton-Antiproton (hadronic) initial state of the Tevatron Collider and the assumption that sparticles are only produced via the LLE term, (connecting (s)lepton fields), sparticles will be produced in pairs via RPC-processes. The strength of the considered RPV-couplings has to be weak, since otherwise we would not be able to reproduce well-known particle properties, like their masses or branching ratios, e.g. the decays of tau leptons. In general, if there is a competition between an RPV-coupling and SM couplings, like those of the SM gauge interactions, the SM couplings will be dominant. Hence, R-parity violation is only visible in the decay of the LSP, which would be absolutely stable in case of RPC-SUSY.

The dominant production process in RPV-SUSY is chargino and/or neutralino pair production through the annihilation of two quarks into a photon, or a Z, or a W boson. Heavier neutralinos and charginos decay predominantly into the LSP (the lightest neutralino) and an associated W or Z boson. The pair of LSPs then decays into at least four leptons via one of the LLE-couplings: λ121, λ122 or λ133.   More leptons ("additional") may be produced via decays of the W or Z bosons.
Note: The RPC-SUSY trilepton analyses can only look for these "additional" leptons as the LSP is stable.

In order to find the desired leptons in the quite large number of mostly hadronic particles produced in each event (see display), we have used the DØ detector, a standard, multipurpose particle physics detector. The necessary sub-systems used to detect leptons are three different kinds of detectors:
  • the tracking detector, which is utilized to precisely reconstruct where a particle came from (its origin, or vertex), its trajectory, and momentum;
  • the calorimeter to measure the energy of charged and neutral particles. Calorimeters are essential for measuring electrons, photons and jets;
  • the muon detector is used to identify muons, distinct from other particles in being minimum ionizing.
    That means, they are the only SM-particles (except the ghost-like neutrinos) able to survive the calorimeter.

    • Events of a particular process are produced more frequently if the cross section for this process, i.e. the effective area is large compared to others. Nevertheless, cross sections in particle physics are tiny, which is why they are usually measured in "barn" with 1 barn (b) = 10-24 cm2. The luminosity, another commonly used variable, is the proportionality factor between the cross section and the produced number of events: N = L⋅σ. A high luminosity leads to a large number of events.

     

      Selection and Analysis of Trilepton Events

    Data collected with the DØ detector from April 2002 to August 2004, corresponding to an integrated luminosity of L∼360 pb-1 was used. Three analyses were developed to search for events containing at least three charged leptons in the following flavor combinations:
    • eel: two electrons and a third lepton: either an electron or a muon
    • µµl: two muons and a third lepton: either an electron or a muon
    • eeτ: two electrons and a tau lepton
    These so-called multilepton events may stem from chargino/neutralino pair production and could hence indicate the existence of supersymmetry. Unfortunately, supersymmetry is not the only source for this type of events; instead they may well be produced from a wide variety of other, already well-known processes such as W or Z boson production. The real work now consists in sorting out, which events are due to known processes and which could possibly have been produced in supersymmetric interactions. The largest and most important sources of "background" events are: Z/γ→ll, W production in association with jets, which may well be misidentified as electrons or taus, diboson production, i.e. WW, WZ, and ZZ, and the pair production of heavy quarks, such as "b anti-b" or "c anti-c". In order to achieve a separation of SUSY candidate events from the large amount of background events, a number of variables with differing distributions for background and SUSY events was analyzed. The following figures show distributions of three different quantities for data (black squares with error bars), the background expected from simulations (coloured histograms) and the expected SUSY signal (solid red lines). Further explanations are given below each of the figures.

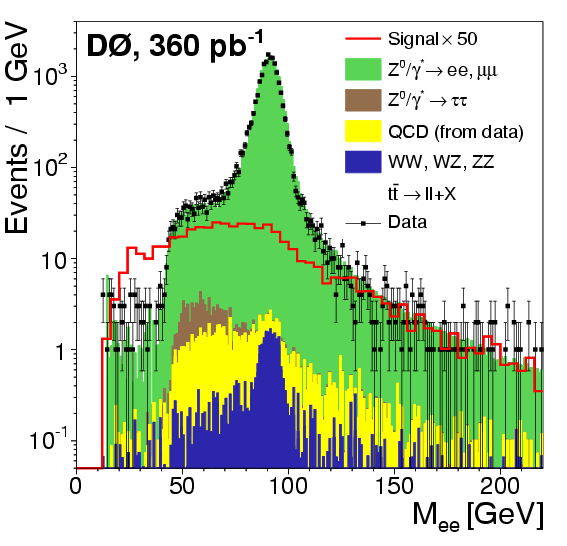
    fig2a fig2b fig2c
    eel analysis: Dielectron invariant mass     (eps)
    This variable corresponds to the mother particle, if no undetectable particles are produced. In case a Z boson is produced and decays into two electrons, the invariant mass of the two electrons describes the mass of the Z boson, consistent with the prominent peak around 80-100 GeV.     		µµl analysis: Missing transverse energy (MET)     (eps)
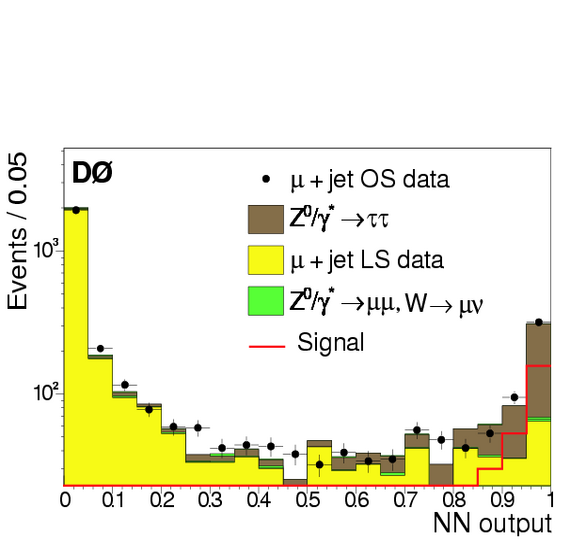
    is not really "missing", but could not be detected due to weakly interacting particles (neutrinos). Due to energy & momentum conservation, the produced particles are expected to be balanced in the transverse plane; an imbalance (MET) indicates undetected particles.     		eeτ analysis: Neural Network (NN) output     (eps)
    for a loose Z→ττ→µτhad selection. This variable serves as identification criterion for tau leptons. A lepton is said to be a tau candidate if NN >0.9 and if its transverse energy deposited in the calorimeter is above 10 GeV.

    Apart from the selection criteria detailed in the above figures a number of further criteria was applied to the data and the simulated backgrounds. The most important ones are thresholds on the transverse momenta (pT) of all three lepton candidates, and requirements on the invariant masses of the two leading leptons in case of the µµl and eeτ analyses. In the µµl analysis, two-dimensional criteria have been applied in the two dimensional parameter regions, defined by: dimuon invariant mass/missing transverse energy (Mµµ, MET), and dimuon angular distance/missing transverse energy (φµµ, MET). For the eeτ analysis, events with invariant masses below 18 GeV and above 80 GeV are excluded to reject as many events as possible from any of the resonances: J/psi, Upsilon (low masses), and W and Z bosons (high masses). Additionally, all three analyses require the presence of moderate missing energy, i.e. in the range of 10-15 GeV.

     

      Results and Interpretation in the context of RPV-SUSY

    After the last stage of the selection, the results of the three analyses are combined in order to achieve the highest possible sensitivity for each λ coupling. As mentioned, we are indeed expecting all kinds of leptons due to the additional leptons, coming from the cascade decays of the produced charginos. The analyses are classified in terms of the signal over background ratio (S/B). Events selected in more than one analysis are assigned to the analysis with the highest S/B ratio and removed from the other analyses. As no excess of events is observed in data, compared to the SM expectations, we set limits at the 95% confidence level (CL). Given the hypothesis that the signal exists, we are hence looking for the maximal cross section the signal can have, so that the SM simulations are still compatible with the observed number of events in data. This is equivalent to testing two hypothesis:
  • hypothesis 1: S+B events from signal and background simulations are needed to explain the observed number of events in data  → CLS+B
  • hypothesis 2: B events from background simulations alone are sufficient to explain the number of data events  → CLB
    • To decide which of the two hypothesis fits better the observed data, we form the ratio of the confidence levels for both hypothesis:
                                            CLS= CLS+B / CLB
    The normalization to the background expectation is done to get rid of its fluctuations. When CLS equals 5%, it defines the value of the signal cross section σ95%CL, that can still be excluded at the 95% confidence level. As no event is observed in data, this is equivalent to calculating only the probablility of having observed zero events, when expecting S events from the signal.

    fig3 fig4
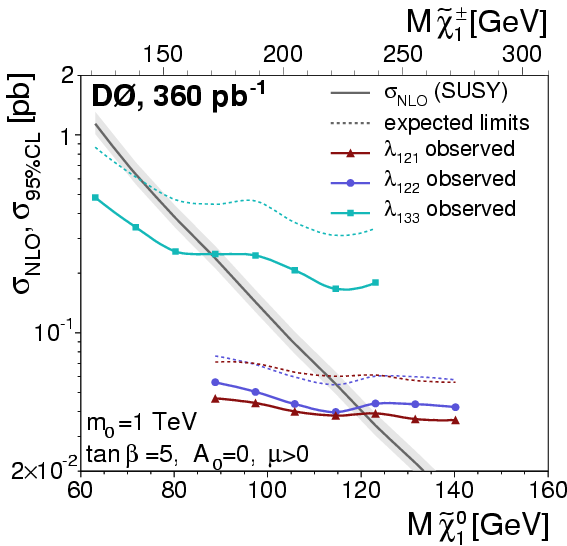
    mSUGRA scenario (m0=1 TeV, tanβ=5, µ>0, A0=0):     (eps)
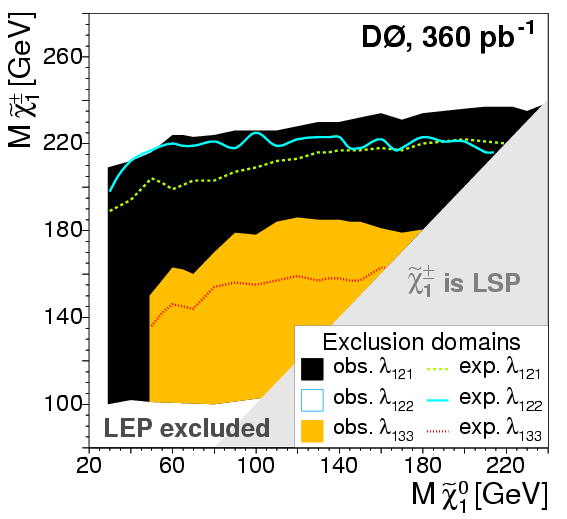
    The next-to-leading order cross section and 95% C.L. limits for the λ121, λ122, and λ133 couplings as a function of the neutralino (chargino) mass. The exclusion domains, lie above the respective observed limit curve.     		no-GUT MSSM scenario     (eps)
    Observed and expected exclusion domains at the 95% CL in the neutralino- chargino mass plane of the considered MSSM model for the λ121, λ122, and λ133 couplings with their strengths set to 0.01, 0.01, and 0.003, respectively

    In the mSUGRA scenario (m0=1 TeV, tanβ=5, µ>0, A0=0), neutralino (resp. chargino) masses up to 119, 118, and 86 GeV (resp. 231, 229, and 166 GeV) are excluded by the three combined analyses for the three couplings λ121, λ122, and λ133, respectively. The lower mass bounds for λ121 and λ122 in case of µ<0 are very similar. A study of the eeτ efficiency dependence on tanβ for the λ133 coupling shows a slight improvement of the lower bounds of ∼10 (20) GeV on the neturalino (chargino) mass. In the no-GUT MSSM model, we exclude chargino masses under 210 GeV (resp. 130 GeV) for neutralino masses greater than 50 GeV (resp. 30 GeV) for the λ121 and λ122, and (resp. λ133) couplings. The cut-off of the exclusion domain towards low neutralino masses is due to the combined effect of the mean decay length of the lightest neutralino (chosen to lie below one cm) and the strengths of the RPV-couplings. Our results are the most competitive to date, compared to the LEP results in the MSSM scenario, where a chargino mass below 103 GeV was excluded for all LLE-couplings, and also compared to the Tevatron Run I results in the mSUGRA scenario.

     
    Text?

    Do you have comments and/or questions about this analysis?
    Please send email to the primary authors: Daniela Käfer, Anne-Catherine Le Bihan, and Anne-Marie Magnan