Search for Neutral Higgs Bosons Decaying to Tau Pairs in p-pbar Collisions at sqrt(s) = 1.96 TeV

Full paper: hep-ex/0605009
Fermilab Result of the Week: May 11 2006

The Higgs boson and the Standard Model

The Higgs boson is a hypothetical particle, which provides a mechanism to give masses to all particles. Scientists know almost everything about it: the way it is created, its decay processes, its charge and there are also predictions about the mass of the Higgs boson. But the most important question is still unanswered: Does it exist?

All matter around us consists of atoms, which in turn consist of a nucleus surrounded by a cloud of electrons. The nucleus is a conglomerate of protons and neutrons, which each have a size of about 10-15 m. But they still contain smaller particles, the so-called quarks. Currently we know that there are six different types of quarks. The interactions of quarks and all other fundamental particles are described by a theoretical framework, called the 'Standard Model'. The Standard Model is an extremely successful theory and has been tested to a high accuracy at previous experiments (for example LEP).

 

Nevertheless we know that the Standard Model can only be an approximation of a more fundamental theory and it gives raise to important unanswered questions, for example: Why are there exactly six quarks or are there more? Why is the heaviest one (the top-quark) about 600 times heavier than the lightest one? Which leads to the question: How do particle get a mass at all? The Standard Model cannot answer these questions without the Higgs boson, since it assumes that all fundamental particles are massless, while in reality the majority of the particles have mass.

 

In 1964 Peter Higgs (from the University of Edinburgh) solved this mystery by introducing a new particle, the Higgs boson, and the corresponding ‘Higgs field’. This field fills the complete Universe and all particles couple (interact) to the Higgs field with a coupling strength that depends on the mass of the particle. The existence of a Higgs boson is a necessity for this mechanism, which is currently the only viable solution consistent with the Standard Model. In this sense the Higgs boson is the keystone of the Standard Model and proving its existence is the main focus of present High Energy Physics.

 

Why Tau Leptons?

The tau lepton is a heavy brethren of the electron. Due to its large mass (approximately 3500 times the mass of the electron) it decays in less than a trillionth of a second after creation into electrons, muons or  hadrons (a bunch of quarks). The tau decay leads also to neutrinos, which are extremely light particles that escape detection. Tau leptons are a rare signal in the data, which needs to be separated from large backgrounds. This requires the use of artificial neutral networks techniques, which are mathematical structures that mimic the way the human brain processes information.

Only one Higgs boson exists within the Standard Model. However there are more complex theories, for example Super Symmetry (SUSY), which predict more than one Higgs boson. If we live in a supersymmetric world (meaning the theory of SUSY is realized), there will be at least five Higgs bosons, two charged and three neutral ones. The three neutral Higgs bosons decay to a large fraction into tau leptons and, depending on how SUSY is realized, the decay into tau leptons can be especially favored.

How do we want to observe the Higgs boson?

At the Fermilab National Accelerator Laboratory (FNAL) beams of protons (the nucleus of hydrogen) and anti-protons (the anti-matter partner) are accelerated to the speed of light and are collided at two interaction points. At the interaction points the decay products of the collisions are observed and recorded by two large detectors (DZero and CDF). The DZero detector has to cope with an amount of about 25 million events per second. A sophisticated trigger system allows reducing the rate to 50 events per second and keeps only events that contain interesting signatures, which e.g. indicate the production of a Higgs boson. We expect a production of a Higgs boson in about 0.0000001% of the initial collisions, making the search for it extremely challenging. To make things even more complicated the Higgs boson decays and has to be detected by its decay products, which can be quarks or other particles of the Standard Model. In the case of the present analysis Higgs decays, which contain a pair of tau leptons are investigated. In order to observe the Higgs-boson, the decay products are used to calculate the mass of the Higgs boson. A signal would stand out as an enhancement above the background from the processes of the Standard Model.

 

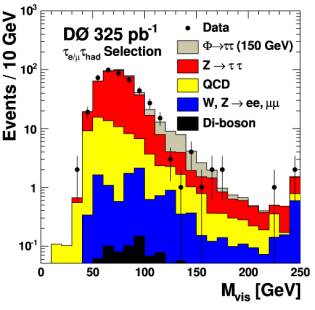
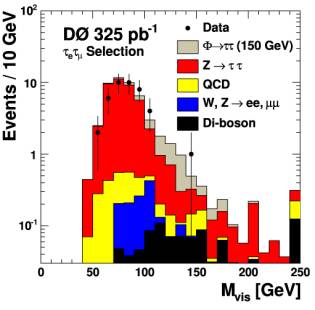
Figure 1. A Feynman diagram showing one possible process, in which a Higgs boson (&Phi) can be produced in proton anti-proton collisions. After the production through the quark loop (b/t) it decays into a pair of tau leptons (&tau).

 

Since tau leptons decay into electrons, muons, or hadrons, three different selections are combined for this analysis. At least one tau lepton is required to decay into an electron or a muon, which leads to three final states: 

1. Tau + Tau → Electron + Hadrons;

2. Tau + Tau → Muon + Hadrons;

3. Tau + Tau → Electron + Muon.

Other possible final states are not considered because they suffer from large backgrounds from processes of the Standard Model. After a selection, which suppresses background while it keeps ‘Higgs like’ events, one calculates the 'combined mass' (invariant mass) of the decay products of the two tau leptons. Since the neutrinos from the tau decays can not be detected directly in the detector, one has to use the ‘missing transverse momentum’ in this calculation. The missing transverse momentum gives the closest possible approximation of the sum of the momentum of the escaping neutrinos. The obtained mass is called ‘visible mass’. The distribution of the visible mass is shown in Figure 2.

For the analysis it is crucial to interpret the measured data in a correct way: Does the data contain only background or is there an indication for a signal from a Higgs boson? This requires having a precise estimate of the expected background. DZero does this by using a sophisticated simulation of the background processes using Monte Carlo techniques. This allows comparing the measured data to the expected background, as shown in Figure 2.

 

 

Figure 2. Distribution of visible mass, which could show a signal of the Higgs boson. The dots represent the measured data, while the shape of a potential Higgs signal is indicated in gray. The other colors stand for different background contributions (first: final states with a hadronically decaying tau lepton, second: final state with only leptonically decaying tau leptons).

 

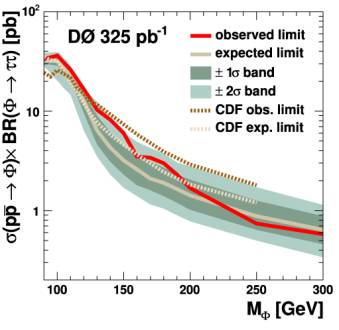
Figure 3. Upper limit on the production rate of the Higgs boson. The horizontal axis gives the Higgs mass in the unit GeV and the vertical axis the production rate in the unit 'pico barn'. The red line indicates the measured upper limit on the production rate of the Higgs boson, while the gray line represents the expectation if there is no Higgs boson (expected limit). If the red line was significantly above the gray one, it would indicate a signal. But in this case the observed limit is well within the errors (shaded areas) of the expected limit. For comparison recent results from CDF are also shown.

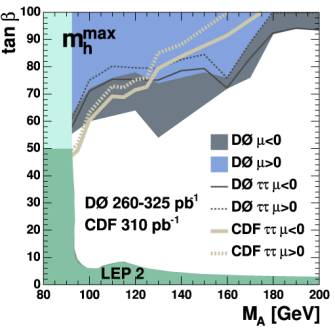
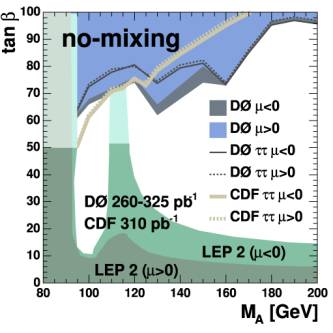
Results

At the end of the selection the data events agree with the expected number of background events. This result can be expressed as un upper limit on the production rate of Higgs bosons. This is illustrated in Figure 3, where the upper limit on the production rate is shown for Higgs masses between 90 GeV and 300 GeV (1 Giga Electron Volt (GeV) = 1.78 × 10-27 kilograms).

The upper limit on the production rate can be interpreted as a restriction on SUSY models. Figure 4 illustrates this restriction for two possible SUSY models. SUSY models, which predict a sufficiently large number of Higgs events above the background, are excluded by this analysis. These restrictions are placed in a combination with a previous search for Higgs bosons performed by DZero.

What do we learn?

The Higgs boson is not yet discovered, but we are getting closer. The obtained limits are currently the best available limits on the production rate of a supersymmetric neutral Higgs boson in the world. DZero will continue to record data and we expect to be able to analyze about 20 times the amount of data that was used in the present analysis. In combination with improving analysis techniques this will lead to tighter and tighter limits on the production rate of the Higgs boson. At the end of this process stands the proof of existence or non-existence of the Higgs boson and a deeper understanding of the Universe we live in.

If you have questions about this analysis, please contact the primary authors Volker Buescher, Carsten Noeding, Maxim Titov, and Ingo Torchiani.

 

 

 

 

Figure 4. Illustration of the excluded regions for two SUSY scenarios. The blue and gray shaded areas indicate the SUSY parameter region, which are excluded by presented analysis in combination with a previous search for supersymmetric Higgs bosons performed by DZero. The black lines correspond to the limit set by the presented analysis alone. The gray lines show limits set by CDF. The green areas are excluded by the LEP experiments.

 

Last change: 05 / 25 / 2006