Matter-antimatter asymmetry and the mixing and decay of beautiful mesons

Date: 19 September 2006
The full DØ publication is available here.
This plain english summary in pdf format is here.

A work of art is neither fully symmetric nor fully random: it has symmetries and asymmetries. Nature itself is an awesome work of art. The laws of nature are full of symmetries and intriguing asymmetries. Today the universe is mostly matter, with only traces of antimatter. When the universe was a fraction of a second old, the asymmetry between matter and antimatter was relatively small: only $(6.1 \pm 0.2) \times 10^{-9}$ . As the universe cooled, matter and antimatter annihilated, leaving the matter we see today.

How did this tiny primordial asymmetry between matter and antimatter arise? Did the universe start out that way, or are the laws of nature asymmetric? The standard model of quarks and leptons does have an asymmetry between matter and antimatter, called CP violation, but it is too small to explain observations. Most extensions of physics beyond the standard model have new sources of CP violation. To understand the origin of the matter-antimatter asymmetry we have to do every experiment we can think of. In this talk I will explain one such experiment.

At the Fermilab Tevatron we collide protons and antiprotons, and observe the particles these collisions produce with the DØ detector. In this measurement, we are interested in rare events with two muons, regardless of the other particles produced. The muon is a particle similar to the electron, but 207 times more massive. The muon $\mu^-$ has negative charge, and the antimuon $\mu^+$ has positive charge. Unlike other particles observed with the DØ detector, the muon can traverse meters of matter. The DØ detector has about 6000 tons of shielding so that muons can be observed with little background from other particles. In our measurement, we count the number $N^{++}$ of events with two positive muons, and the number $N^{--}$ of events with two negative muons, and calculate the dimuon charge asymmetry

$$A = \frac{N^{++} - N^{--}}{N^{++} + N^{--}}.$$ (1)

To understand why this measurement is interesting, I will explain the phenomenon of mixing exhibited by two beautiful mesons, $B^0$ and $B^0_s$ . The $B^0$ meson is composed of a $d$ (or down) quark and a $\bar{b}$ antiquark. Its antiparticle $\bar{B}^0$ is composed of a $b$ (or beauty) quark and a $\bar{d}$ antiquark. The $b$ quark may decay as $b \rightarrow \mu^- c \bar{\nu}_\mu$ , while the $\bar{b}$ antiquark may decay as $\bar{b} \rightarrow \mu^+ \bar{c} \nu_\mu$ (where $c$ is the charm quark, and $\nu_\mu$ is a particle, called neutrino, that traverses the DØ detector leaving no trace to be observed). The $B^0$ can decay to a muon and anything else, without mixing, $B^0 \rightarrow \mu^+ X$ , or with mixing, $B^0 \rightarrow \bar{B}^0 \rightarrow \mu^- X$ . The X stands for "anything else". Similarly, the $\bar{B}^0$ can decay to a muon and anything else, without mixing, $\bar{B}^0 \rightarrow \mu^- X$ , or with mixing, $\bar{B}^0 \rightarrow B^0 \rightarrow \mu^+ X$ . Similar decays are exhibited by $B^0_s$ and $\bar{B}^0_s$ (with the $d$ quark replaced by the $s$ quark).

At the Fermilab Tevatron, beauty quarks are produced in $b \bar{b}$ pairs. The $b$ quark hadronizes 40% of the time into a $\bar{B}^0$ mesons, 11% of the time into a $\bar{B}^0_s$ mesons, and the remaining 49% of the time into beautiful hadrons that do not mix.

Consider events with two beautiful hadrons, one created with a $b$ quark and one created with a $\bar{b}$ antiquark. Further, consider events in which both $b$ and $\bar{b}$ decay to a muon plus anything else. If one of the beautiful hadrons decays with mixing, and the other decays without mixing, we obtain a like-sign dimuon event. If the mixing and decay $B^0 \rightarrow \bar{B}^0 \rightarrow \mu^- X$ has a different probability than the mixing and decay $\bar{B}^0 \rightarrow B^0 \rightarrow \mu^+ X$ , we obtain a dimuon charge asymmetry $A$ . In the standard model the asymmetry $A$ is tiny: about $\vert A_{B^0} \vert \approx 10^{-3}$ for $(B^0, \bar{B}^0)$ decays, and $\vert A_{B^0_s} \vert \approx 10^{-4}$ for $(B^0_s, \bar{B}^0_s)$ decays.

Mixing is due to box Feynman diagrams. New particles of physics beyond the standard model can participate in additional box diagrams, and therefore alter the frequency of $B^0 \leftrightarrow \bar{B}^0$ or $B^0_s \leftrightarrow \bar{B}^0_s$ mixing, and produce a dimuon charge asymmetry $A$ . Therefore a good place to look for certain extensions of the standard model, is to measure the frequency of mixing (which, unfortunately, suffers from large theoretical uncertainties), and the dimuon charge asymmetry $A$ . Some extensions of the standard model, compatible with all other observations, predict asymmetries that we can observe. Conversely, if we measure an asymmetry consistent with zero, we can constrain these models.

Let us now consider the measurement of the asymmetry $A$ . The first worry is an instrumental asymmetry due to the offset of the mean beam spot position, and other asymmetries of the detector. This instrumental asymmetry is measured to be approximately 0.006, and changes sign when the toroid magnetic field is reversed, see the Figure. These reversals are done roughly every two weeks. By averaging the asymmetry $A$ measured with one toroid polarity, with the asymmetry $A$ measured with the opposite toroid polarity, it is possible to cancel these first order detector effects. After averaging, we are left with a systematic uncertainty of $A$ , due to instrumental effects, less than $0.00023$ in absolute value.

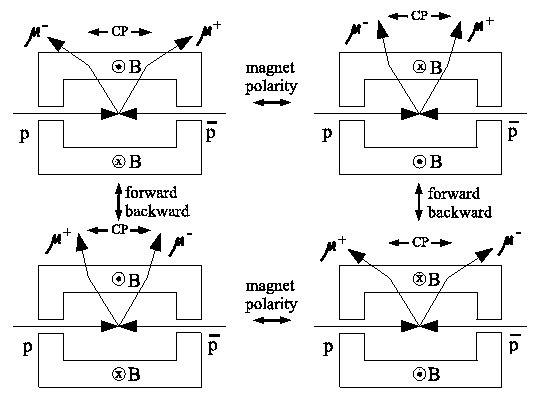
Schematic drawing of the magnetized iron toroids of the DØ detector, and muon tracks related by toroid polarity reversal, CP conjugation and forward-backward reflection.

Kaon decay, $K^\pm \rightarrow \mu^\pm X$ , in coincidence with a muon from the collision, is an important background. The interaction length of $K^+$ in the calorimeter of the DØ detector is longer than the interaction length of $K^-$ . Therefore $K^+$ has more time to decay than $K^-$ . The result is a charge asymmetry from $K^\pm$ decay. To the measured dimuon charge asymmetry we add a correction $-0.0023 \pm 0.0008$ due to the asymmetric kaon decay background.

Including additional uncertainties (from cosmic rays, miss measured muon charge, and punch-through of hadrons that are reconstructed as a muon) we obtain the corrected dimuon charge asymmetry:

$$A = -0.0028 \pm 0.0013\textrm{(stat)} \pm 0.0009\textrm{(syst)}.$$ (2)

Note that the systematic error is dominated by the uncertainty of the correction due to the kaon decay background.

The asymmetry $A$ at the Tevatron $p \bar{p}$ collider has contributions from mixing in both $B^0$ and $B^0_s$ systems, and is diluted by the beautiful hadrons that do not mix, and by $c$ and $s$ quark decays. Our final result is

$$A_{B^0} + 0.72 A_{B^0_s} = -0.0092 \pm 0.0044\textrm{(stat)} \pm 0.0032\textrm{(syst)}.$$ (3)

In comparison, the world average in the PDG Particle Physics Booklet of 2004 is $A_{B^0} = 0.002 \pm 0.0124$ , and no limit is given for $A_{B^0_s}$ . See the full DØ publication for more details.

In conclusion, the result (3) is the most stringent measurement of its kind in the world, is compatible with the standard model, and constrains some of its extensions. The general result (3) complements measurements at $B$ -factories which are sensitive only to $A_{B^0}$ , not $A_{B_s^0}$ .