Directly determined limits on the B_s meson mixing frequency

A peculiar and extremely important property of neutral B mesons is that they can spontaneously transform themselves into their own antiparticles (and visa versa). This phenomenon, known as flavor oscillation or mixing, has been measured in the B_d system (a bound state of a b-antiquark and a d-quark), but remains to be observed for B_s mesons (b-antiquark and s-quark bound states), which oscillate at a much faster frequency. One of the major goals of the DØ experiment is to measure the B_s oscillation frequency. This measurement will provide a crucial and unique test of our understanding of nature’s weak force, and could provide indirect evidence for new fundamental particles and interactions.

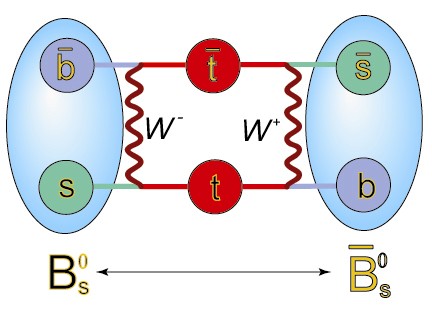
Figure 1: The B_s mixing "box  diagram" (antiparticles are denoted by a bar above their symbol). The B_s meson, shown on the left, transforms (or oscillates) into its own antiparticle by exchanging a W-boson (the wavy line) between its constituent b-antiquark and s-quark, producing a top-quark top-antiquark pair which quickly exchange another W-boson, producing a s-antiquark and a b-quark: the antiparticle of the B_s. 

The B_s meson mixes via the weak interaction between its own constituents. This process (shown in Figure 1), involves the exchange of a W-boson between the original b-antiquark and s-quark which produces a top, anti-top quark pair, which is almost immediately transmuted by another W-boson exchange into a b-quark and s-antiquark pair (an anti-B_s meson). The rate at which this transformation occurs is characterized by the mass difference between the two quantum states of the meson, called Δm_s.  We know, from previous experimental attempts to measure this frequency, that Δm_s is greater than 16.6 ps^-1 (16.6 trillion times a second). The Standard Model of particle physics predicts that Δm_s is between 16.7 ps^-1 and 25.4 ps^-1.

It is extremely difficult to measure oscillations this rapid. B_s mesons are unstable and quickly decay into lighter particles. They travel at most a millimeter or two before they decay, and we must measure this distance very precisely. A precision on the order 10's of microns is needed to be able to measure the mixing frequency. We also must determine the momentum of the meson by detecting as many of its decay products as possible. Finally, in order to see if a B_s meson has mixed, we must determine its flavor (whether or not it is a particle or antiparticle) at both the time it was produced and when it decayed. Its flavor at decay time is determined by the charge of its decay products. Since b-quarks and b-antiquarks are almost always produced in pairs in collisions at the Tevatron, the B meson's flavor at production can be determined by a partial reconstruction of its partner b-hadron which is on the opposite side of the event. We used our large samples of hundreds of thousands of reconstructed B mesons to optimize and calibrate this opposite side flavor tagging procedure. We have measured the well known B_d meson oscillation frequency using this flavor tagging and obtain the correct result. This gives us confidence that our flavor tagging and other techniques are sound, so we move on to attempt a measurement of B_s mixing.

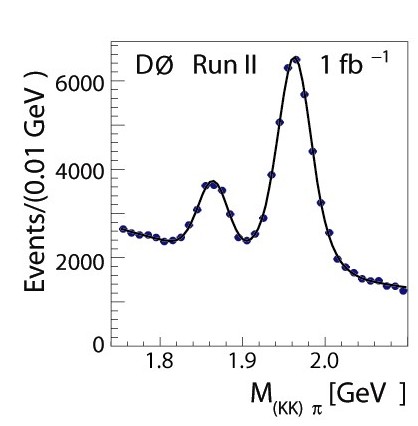
Figure 2: Invariant mass distribution of the kaon-kaon-pion system. The peak on the right correspond to the decay of Ds mesons. There are 27,000 events above background in this mass region.

In this analysis, we look for events in which the B_s decays into a D_s meson (a c-antiquark, s-quark bound state) plus a muon and a neutrino. We choose this decay mode because it has a muon in the final state which is easy to detect and rarely produced in high energy particle collisions. This allows us to pick out (or “trigger” on) these type of events from the millions of collisions per second produced by the Tevatron. Using this decay mode comes at a price, however, as the neutrino passes through our detector without leaving a trace. This makes the determination of the B_s momentum less precise as we are missing one of its decay products. The D_s meson is also unstable and decays into a phi meson plus a pion in a short period of time. The phi meson decays immediately in two kaons. We look for three particle tracks in our detector near the muon and add up their momentum in a relativistic manner determining the invariant mass of the system. If the particles are from the decay of a D_s meson, their invariant mass should equal the rest mass of the D_s. The invariant mass distributions in our data for this selection are shown in Figure 2. The large peak on the right corresponds to D_s decays. After four years of taking data, we have reconstructed twenty seven thousand D_s mesons in this decay mode. Most of these are from B_s decays, and in six thousand of them we are able to determine the initial flavor of the B_s. The intersection of the reconstructed D_s flight path with that of the muon gives us the distance the B_s meson traveled before it decayed. This, along with its momentum measurement (how fast it was traveling), gives the lifetime of the B_s meson.

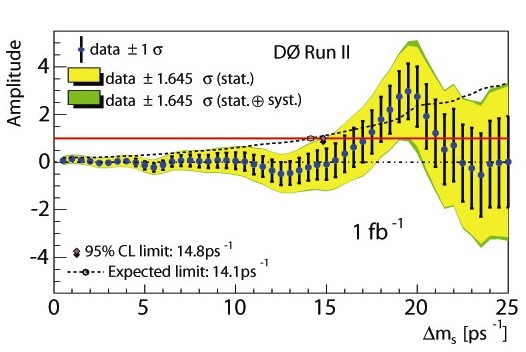
Figure 3: This plot shows the "amplitude scan" of the mixing frequency of our data. For each value of Δm_s (horizontal axis) an amplitude value A (vertical axis) is determined (the yellow and green bands represent the uncertainty in this determination). The value of A should be one (shown as a red line) if the data are compatible with the given mixing frequency, and zero otherwise. The data clearly deviates from zero around for values of Δm_s around the peak at 19 ps^-1 indicating the presence of oscillations with frequencies in the range where the uncertainty band is above zero.

The probability for an initial B_s meson to mix and decay as an anti-B_s meson as a function of its lifetime (t) is proportional to a simple mathematical form 1-Acos(Δm_s t).  The probability for it to not oscillate is proportional to 1+Acos(Δm_s t). For a perfect detector and flavor tagging algorithm, A (the amplitude) would be equal to 1. Of course, nothing is perfect, but we know our detector and algorithms well enough to correct for their inefficiencies and resolutions.  We perform a sophisticated multi variable mathematical fit of our data taking these corrections into account and determine the amplitude and its uncertainty for various values of Δm_s; scanning from 0 to 25 ps^-1. The amplitude should be zero (within uncertainties) for the incorrect values of Δm_s and then peak at 1 (within uncertainties) for the correct value. As you can see in Figure 3, the “amplitude scan” shows a peak in the amplitude for values of Δm_s around 19 ps^-1, indicating the presence of oscillations at (or near) this frequency.

In order to pin down the oscillation frequency more precisely we perform an even more refined fit to the data. Again a scan of Δm_s is performed, but in this fit the amplitude A is set equal to 1. The fit returns a probability or “likelihood” that the data fits the mixing probability functions. The results of this procedure tell us that the most likely value of Δm_s is 19 ps^-1 and more importantly that Δm_s is in the range 17 < Δm_s < 21 ps^-1 at the 90% confidence level. This is the first directly determined range for the B_s oscillation frequency, and it fits quite well within the Standard Model predictions. It is still, however, very important that we make a precise measurement of the B_s oscillation frequency. We are already working on improving our analysis by using more B_s decay modes, developing additional flavor tagging algorithms, and adding a more precise inner particle tracking detector.

An article on this analysis has been submitted to Physical Review Letters in March 2006.

For more information on this analysis please contact the DØ Bs mixing group via the  physics coordinator.